关联规则-Apriori算法

关联规则

关联分析：用于发现隐藏在大型数据集中的有意义的联系，所发现的联系可用关联规则或频繁项集的形式表示。

应用领域：购物篮数据/科学数据分析/网页挖掘

本节讨论购物篮数据。

许多商业企业在运营中积累了大量的数据，如食品商店的收银台每天都收集大量的顾客购物数据，如表1所示，通常称为购物篮事务，每行对应一个唯一表示TID和给定顾客购买的商品集合，分析这些数据的关系可以用于市场促销，库存管理和客户关系管理等。

对购物篮数据进行关联分析面对的问题：

1) 从大型事务数据集中发现模型在计算上可能付出的高代价（挖掘算法）

2) 所发现的模式可能存在虚假（评估问题）

一、基本定义

1）二元表示

原表1购物篮事务的二元表示如表2：

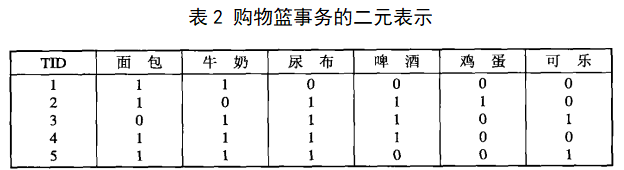
 2）项集：记为购物篮数据中所有项的集合，为所有事务的集合。包含0或多个项的集合称为项集，一个TID对应一个事务，事务包含的项集为I的子集；例如：表1中TID=2对应第二个事务{面包，尿布，啤酒，鸡蛋}，包含项集{面包，尿布}，不包含项集{面包，牛奶}。

3）事务的宽度：事务中出现项的个数，如第2个事务的宽度为4。 

4）支持度数：包含特定项集的事务个数，项集X的支持度数可表示为：

 

如项集{啤酒，尿布，牛奶}的支持度数为2。

5）关联规则：形如X->Y的表达式，且X∩Y=Ø。关联规则的强度可以用支持度（support）和置信度（confidence）度量。

   支持度（s）：X与Y同时出现的事务在T中的比例，确定规则可以用于给定数据集的频繁程度；

      置信度（c）：X与Y同时出现的事务在X出现的事务中的比例，衡量Y在包含X的事务中出现的频繁程度:

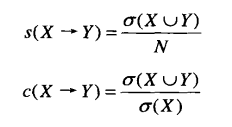
注：由关联规则作出的推论并不必然蕴涵因果关系。

2）关联规则发现：给定事务的集合T，关联规则发现是指找出支持度大于等于minsup且置信度大于等于minconf的所有规则。

注：从包含d个项的数据集提取的可能规则的总数为：

推到如下：设左边项有k个，则右边项有d-k个:

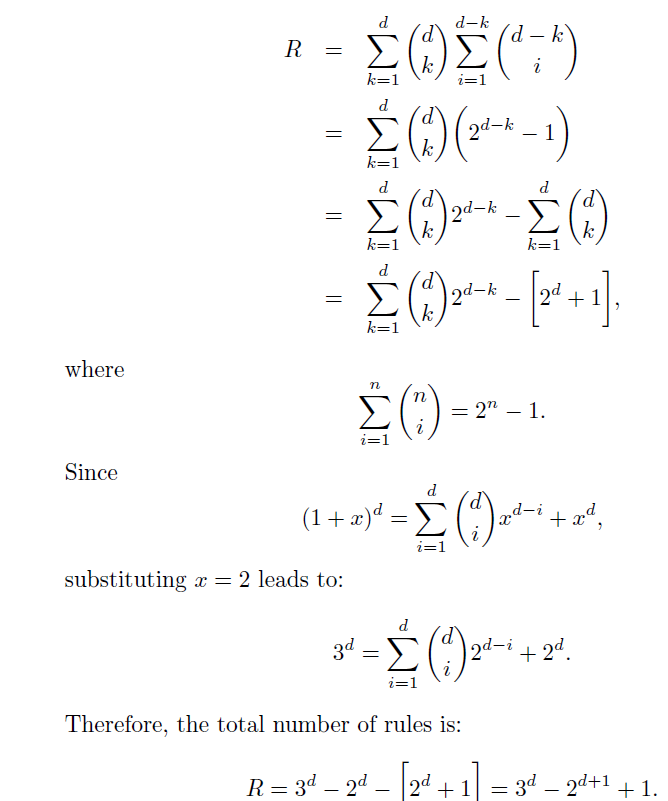
由于原始方法挖掘规则的计算成本很高，因此，大多数关联规则挖掘算法通常采用的一种策略是，将挖掘任务分解为如下两个子任务：

①　频繁项集产生：发现满足minsup的所有项集（频繁项集）。

②　规则的产生：从上一步发现的频繁项集中提取所有高置信度的规则（强规则）。

 

一、频繁项集的产生

1. Apriori算法

Apriori（先验）原理：如果某个项集是频繁的那么它的所有子集也是频繁的。

相反，若一个项集是非频繁的，则它的所有超集也是非频繁的，则整个包含非频繁集的超集的集合可以被立即剪枝，这种策略称为基于支持度的剪枝。

Apriori算法流程：

1) 单编扫描数据集，确定每项的支持度，得到所有频繁1-项集；

2) 使用上一次迭代发现的频繁（k-1）-项集，产生新的候选k-项集，候选的产生使用apriori-gen函数实现。

3) 对候选项的支持度进行计数；

4) 删去支持度计数小于minsup的候选项集；

5）当没有新的频繁项集产生，结束。

候选产生过程： 

1) 蛮力方法

将所有的k-项集都看作可能的候选，再进行剪枝。设d为项的总数，则每一层产生k-项集的数目为，总复杂度为。

2) 方法

用其他频繁项来扩展每个频繁（k-1）-项集，产生个候选k-项集，总复杂度为.

3）方法

 函数apriori-gen的候选产生过程合并一对频繁（k-1）-项集，仅当它们的前k-2个项都相同。

 例：{面包，尿布}+{面包，牛奶}={面包，尿布，牛奶}

 注：算法不合并{啤酒，尿布}和{尿布，牛奶}，因为它们的第一个项不同，这种使用字典序的方法是为了避免重复。

支持度计数：

1）法一：将事务与所有的候选项集进行比较，并且更新包含在事务中的候选项集的支持度计数，此方法在当事务和候选项集的数目都很大时计算成本很高。

2）法二：枚举每个事务所包含的项集，利用它们更新对应的候选项集的支持度。

如下为事务t获得3-项集的方法：假定每个项集中的项都以递增的字典序排列，则项集可以这样枚举：先指定最小项，其后跟随较大的项。例如，给定事务{1 2 3 5 6}，它的所有3-项集一定是以项1，2，3开始，不必构造以5或6开始的3-项集。

 

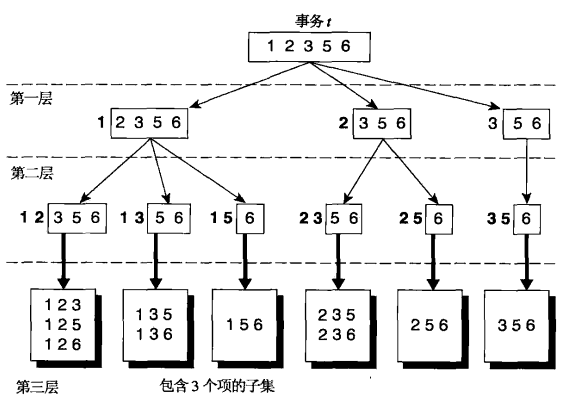
枚举完候选项集后，还必须确定每一个3-项集是否对应一个候选项集，若它与一个候选匹配，则相应候选项集的支持度计数增值，下边利用hash树来进行匹配操作：

在Apriori算法中，候选项集划分为不同的桶，并存放在Hash树中，在支持度计数期间，包含在事务中的项集也按照相同方式散列到相应的桶中，此法中只需将事务中的每个项集与同一桶内候选项集进行匹配，而不必和所有候选项集进行比较，这就是Hash树的优势。

Hash树建立：https://blog.csdn.net/owengbs/article/details/7626009

假设构建一棵Hash树，树的每个内部结点都使用hash函数h(p)=p mod 3来确定应当沿着当前结点的哪个分支向下，且每个叶子节点最多含有三个项集，如果插入某一节点的项多余3项，需要进行分裂操作，把原来的3项集和新的项集以第2项做hash，映射到新的叶节点，此例待插入的项共有15个。

• 候选项集的Hash树建立：

 

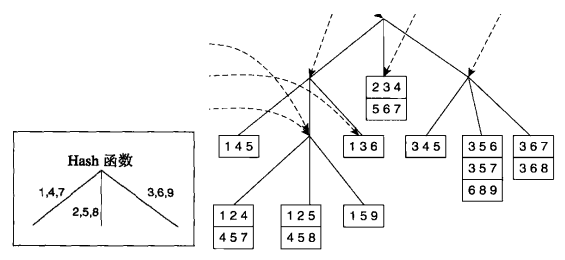
• 事务的Hash树建立：

 

 

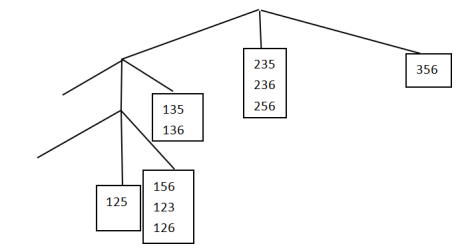
• 匹配更新支持度数：

 

 

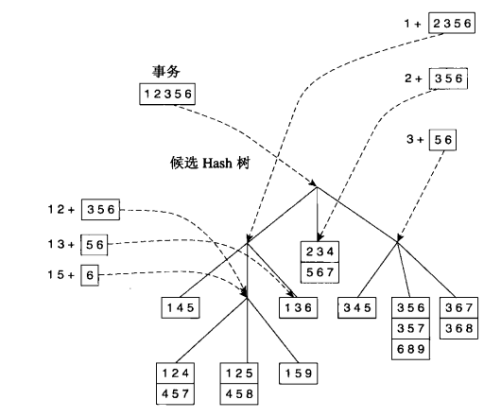
规则的产生：

• 提取方法

将项集Y划分为两个非空子集X和Y-X，使得X->Y-X满足置信度阈值。

注：这样的规则必然已经满足支持度阈值（由频繁项集产生），且计算规则的置信度不需要再次扫描事务数据集（项集的支持度计数已在频繁项集产生时得到）。

• 基于置信度的剪枝

定理：若规则X->Y-X不满足置信度阈值，则形如的规则一定也不满足置信度阈值，其中。

• Apriori规则的产生

Apriori算法使用一种逐层方法来产生关联规则，其中每层对应于规则后件中的项数，初始提取规则后件只含一个项的所有高置信度规则，然后使用这些规则来产生新的候选规则。下图显示由{abcd}产生关联规则的格结构。

 

2、FP增长算法

1）FP树表示

FP树是一种输入数据的压缩表示，它通过逐个读入事务，并把每个事务映射到FP树中的一条路径来构造，对于不同事务中相同的项，它们的前缀路径相同。路径相互重叠越多，使用FP树结构获得的压缩效果越好。

2）构建FP树：

初始，FP树仅含一个根节点，用null表示，随后：

①　扫描一次数据集（第一次扫描），确定每个项的支持度数，找出频繁1-项集，将含非频繁1-项集的事务去掉。

②　扫面一次数据集（最后一次扫描），把剩下的事务逐个按照支持度先进行排序再依次插入到FP树中（为了共用前缀）。

③　建立同项的链表并创建header-table。

例：有如下购物篮数据：

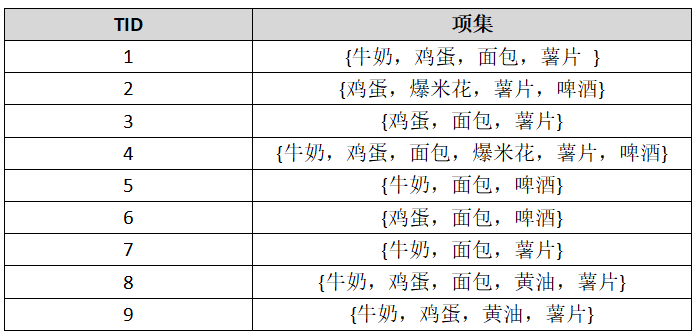
假设minsup=3，以此建立一棵FP树。

计算每个项的支持度计数：

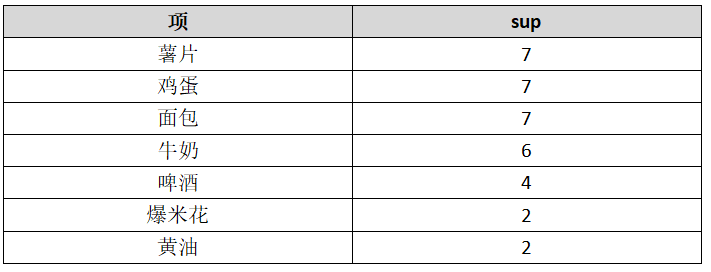
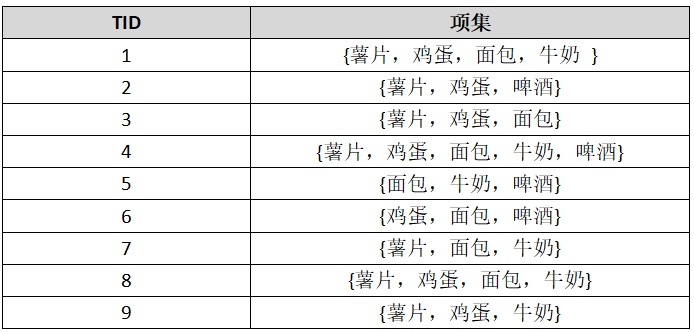
删去非频繁1-项集：爆米花，黄油，按支持度计数大小降序将事务排列如下：

建立FP树如下：

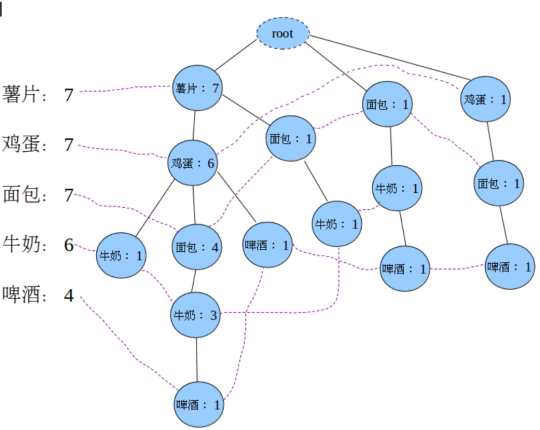
注：FP树的大小取决于项的排序方式，如果颠倒前面例子的序，即升序，则树会更加茂盛。

 

1）频繁项集产生

①　从FP树的最下面的项开始，构造每个项的条件模式基（CPB）：该项到根节点之间的FP子树（利用链表可快速查找路径）。

②　对每个CPB，将所有的祖先节点计数设置为叶子节点的计数，累加每条CPB的支持度计数，去掉不符合minsup的项，构建条件FP树。

③　递归挖掘每个条件FP树，累加后缀频繁项集，直到FP树为空或FP树只有一条路径。

接上例：

寻找啤酒的频繁项集

啤酒的CPB：{薯片：1，鸡蛋：1，面包：1，牛奶：1}

                      {薯片：1，鸡蛋：1}

                      {面包：1，牛奶：1}

                      {鸡蛋：1，面包：1}

 去掉不满足支持度计数的薯片，牛奶，构建条件FP树：

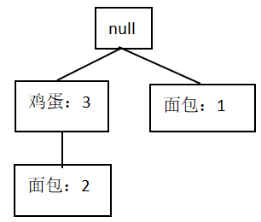
以啤酒结尾的频繁项集：{啤酒：3}、{面包：3，啤酒：3}、{鸡蛋：3，啤酒：3}

以面包，啤酒结尾的频繁项集：{鸡蛋：2，面包：2，啤酒：2}不符合minsup

以鸡蛋，啤酒结尾的频繁项集：{null，鸡蛋：3，啤酒：3}，终止。

得到啤酒的频繁项集：{啤酒}，{面包，啤酒}，{鸡蛋，啤酒}

寻找牛奶的频繁项集…

三、关联规则的评估

1、支持度-置信度框架的局限性

支持度的缺点：许多潜在的有意义的模式由于包含支持度小的项而被删去，比如很少人购买珠宝，但关于它的关联规则可能是商家所关心的。

置信度的缺点：高置信度并不代表规则是有意义的，往往是因为忽略了后件的支持度数。

常用评判准则：

• 提升度（lift）：

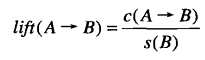
对于二元变量，上式等价于如下兴趣因子：

结果可解释如下：

 

•  IS度量

IS用于处理非对称二元变量，定义如下：

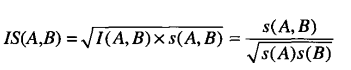
当兴趣因子和支持度都很大时，IS也很大。另，可证明IS等价于二元变量的余弦度量：

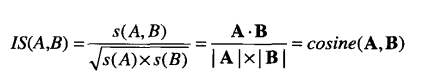
IS也可以表示为从一对二元变量中提取出的关联规则的置信度的几何均值：

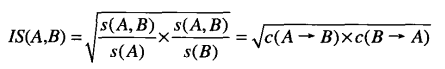
由于两个数的几何均值总是接近较小的数，所以只要规则A->B或B->A中的一个具有较低大的置信度，项集{A,B}的IS值就较低。

 

 

 

 

 

 

 

 

 

 

 

---恢复内容结束---