算法知识还是需要地……

一般情况，我们遇到真正的算法问题，似乎并不多，大都是检索、增删改之类的操作和功能点，只要对语言，如 JavaScript 和 C# 或 Java 特性足够了解，都很容易解决。但若是遇到真正的算法问题，足够让人想两三天的。此时，就是体现你价值的地方啦……

其实，本文内容并不新鲜，只是重新整合后，会呈现出不同的意义。通过两个计算，展示程序员不能忽视算法方面的知识，如何利用分治法、动态规划、贪心算法等思想设计自己的算法，并能大概分析，了解其“瓶颈”，在何种情况下，运行效率最好。

你可以是什么都懂的程序员，可别人不用听你口若悬河地大谈各种技术，只要看下你的代码，就知道了。

最近，编写一个工厂生产过程中变更工艺的算法。关键是，无论工艺怎样变更，数量不能错（包括零件数量、可排序数量、已排产数量、返修数量、报废数量）。甲方认为几乎不能实现。因为，变更的情况太多，几乎无法处理，即便处理了，算法的判断会不计其数。表面看起来的确如此，但从数学上，如此多的情况都可以合并成一个计算公式，只要找到它。再利用一点算法的知识，在递归条件上考虑一下。最后的核心算法：三个递归函数，每个函数不过 10 行，显得很优雅。而且，通过把代价考虑进去，可以扩展该算法。

在此之前，2008 年毕业，我使用 VS C# 开发 Web 应用程序……到 2012 年，只跳槽一次。这期间，我写过较复杂的算法，是在之前公司做的一个关于解析数据的功能和算法。因此，当我愤然离职后，决定将核心算法的备注删掉一半。皮鞭蘸凉水，累死你们，呵呵～～

数据是关于气象、水文、台站、浮标、生物、化学、重力、磁力、地球物理、悬浮体等这些基础数据，6 个大类，里边的小类无数……这些数据都是由相关器械采集并生成的 DAT 文件，特点：

• 每种数据有自己的书写格式；
• 有横向书写，也有竖向书写；
• 用 UltraEdit 查看，每列有具体的含义；
• 数据有详细、严格的要求，比如精度、长度、科学计数法等；
• 数据后面有单位符号；  
• 多个行的数据可能存在关系。因为，DAT 数据对应数据库多个表等等。

这个功能用策略模式。用反射创建相应的解析器。关键是将数据库中的数据恢复成 DAT 文件的算法。将数据格式设置成 XML 文件（XML 文件是 DAT 文件与数据库表和字段的映射关系），既要递归格式，也要递归数据；另外，还要设置队列，递归前或递归后，要对数据进行处理等等。

 

问题一

---

我们知道插入排序和合并排序的时间复杂度分别为 O(n^2) 和 O(nlgn)，后者比前者增长的慢。因此，当输入 n 规模越来越大时，合并排序比插入排序会有更好的效果。

假设，在同一台机器上比较插入排序和合并排序的实现。若输入规模为 n，前者要做 8n^2 步，后者要做 64nlgn 步。那么，n 取何值时，插入排序将优于合并排序？

其中，

• “”表示“等价于”；
• “”是超越方程（transcendental equation）。这样的方程存在无法用自变量的多项式或开方表示的函数。超越方程无法利用代数几何来求解，沒有一般的求解公式，也很难得到解析解。与超越方程相对的是代数方程。但可以写程序解这个不等式方程。

// 显然 n 从 2 开始
int n = 2;
double insert = Math.Pow(2, n);
double meger = Math.Pow(n, 8);

while (insert <= meger)
{
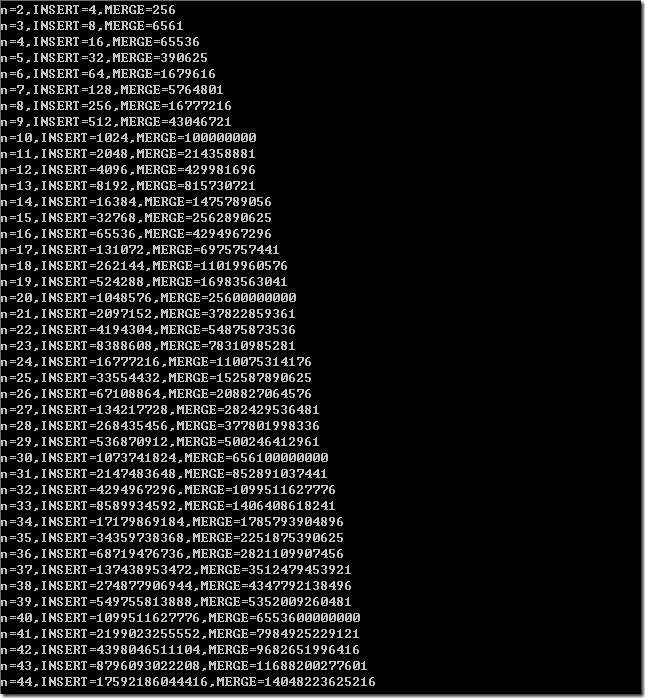
    Console.WriteLine(string.Format("n={0},INSERT={1},MERGE={2}", n, insert, meger));
    n++;
    insert = Math.Pow(2, n);
    meger = Math.Pow(n, 8);
}
Console.WriteLine(string.Format("n={0},INSERT={1},MERGE={2}", n, insert, meger));

当 n=44 时，插入排序的步骤就开始大于合并排序。因此，n 为 [2,43]。

 

问题二

---

上面，当输入 n 规模不断变大时，插入排序和各并排序的差异。因此，往往为解决同一个问题而设计的各种算法在效率上会有很大差异。这些差异可能比个人微型计算机与巨型计算机之间的差异还要大。

例如，让一台巨型计算机做插入排序，而让另一台微型计算机做合并排序，它们的输入都是一个长度为 10^6 （100 万）的数组。假设，巨型计算机每秒执行 10^8 （1 亿）条指令，微型计算机每秒仅仅为 10^6 （100 万）条指令。为了使差异更明显。假设，世界上最优秀的程序员用机器代码在巨型计算机上实现插入排序，编写的程序需要执行 2n^2 条指令排序 n 个数。另一方面，让一个一般程序员在微型计算机上用高级语言编写合并排序，代码要执行 50nlgn 条指令。

为了排序 10^6 万个数，巨型计算机耗时：

而个人微型计算机耗时：

可以看出，由于采用更低阶的算法，即使是用低效的编译器，微型计算机还是比巨型计算机快 20 倍。

备注：

对数以 2 为底。