思考机器（一）——计算机是怎样进行逻辑思考的

 

上个世纪九十年代，人工智能曾是计算机研究领域的热门。当时AI发展的重点在于用形式系统模拟人脑的逻辑思维，即如何用符号表示推理法则，再令机器像人脑一样运用规则进行推演与判断。这类AI在短暂的喧嚣后归于沉寂，除了在数学考场上，多数情况下人脑对事物的判断，是源于大量经验累积中涌现的直觉，而非严密的逻辑推理。

 

到了新世纪，人工智能再度成为热门话题，如今的AI几乎已经是神经网络的同义词。也许无论是硅基还是碳基系统，真正的智力在于学习新知识的能力，而非对于知识的表达与运用。相比今天的人工智能，传统的形式系统只应用于某些特定领域，如计算机辅助证明，程序的形式化验证等等。然而，这不表示形式化已经是过时的知识。理解形式系统的思想，尤其是与之密切相关的类型系统，不仅有助于正确的程序语言表达，更能理解代码的本质。本文简单讨论一下形式化验证的基石——柯里-霍华德同构，以此来说明计算机为什么可以进行逻辑推理，以及计算机是怎样进行逻辑推理的。

 

一、什么是逻辑？什么是形式？

 

三段论奠定直觉逻辑

——“苏格拉底是人，人会死，所以苏格拉底会死”

 

讨论为什么之前，先说是什么。最古老的逻辑可以追溯到三段论，即所谓直觉逻辑。在苏格拉底这个例子中，每一句陈述由一个主语（苏格拉底，人）和一个谓词（是人，会死）组成。其中“人”、“死”可以看作所陈述的主语的特性。

 

主语与特性之间用什么系词来表达，不影响对陈述的理解。在自然语言中，我们可能说苏格拉底是人；苏格拉底系人；苏格拉底者，人也。这种依靠自然语言的表达并不严谨，以致完全不同的陈述可能表达同一意义，反之同一陈述也可能有不同的理解。因此，逻辑学家们选择使用统一的抽象符号，并赋予其严格的含义与推导规则，例如，四则运算的符号与法则就是放诸四海而皆准的。在苏格拉底这个例子中，我们可以用➞来表达“是”、“会”这一表示属性的词汇，用⇒表示“所以”，“导出”这类蕴涵着推理关系的词汇：

 

((苏格拉底➞人) and (人➞死))⇒(苏格拉底➞死)

 

在直觉逻辑的世界中，这是一个特定的表达式。在这个特例里，如果我们将所陈述的对象苏格拉底完全替换为柏拉图，并不影响表示式的正确性。如果我们用符号S代替苏格拉底，用符号H代替人，用符号D代替死，将and简化为符号×，以上的将例子进一步抽象为

 

((S➞H)×(H➞D))⇒(S➞D)

 

此处的S/H/D不再是具体的事物或特性，而是一个变量。将该变量替换为任何人事，在逻辑上都是成立的。比如令S=苹果，H=水果，D=好吃，可以得出陈述

 

((苹果➞水果)×(水果➞好吃))⇒(苹果➞好吃)

 

因此，((S➞H)×(H➞D))⇒(S➞D)不再是一个具体的陈述，而是一条抽象的推理法则。苏格拉底则是这条法则的一次应用。

 

如果我们给一个三段论运算器编入这一法则，再提供形如(S➞H)和(H➞D)两个陈述，它总是可以得出形如(S➞D)这一结论。通过定义严格的语法与推理规则，构建起一个推演系统的过程，称作形式化，该系统即形式系统。

 

举例来说，数学就是一种形式系统。在自然语言中，我们可能将一个计算描述为二十乘以三十，三十个二十，twenty times thirty等等。但是使用数学语言时，全世界小学及以上文凭的人都会将这个计算过程表述为 20×30=600

 

形式与意义是相对独立的

——玄之又玄，众妙之门

 

在形式系统中，重要的是推理规则，而不是名字和符号。在上述苏格拉底的例子，将同一个表达式中的事物名换为其他符号，完全不影响推理的过程。

 

举例来说，(S➞D)既可以用作人类学表述，即苏格拉底会死；也可以用作饮食文化陈述，即苹果好吃。我们只需要将S和D等量替换为不同的叙述对象就行了。甚至在某个星球上，“苏格拉底”指一种红红的，圆圆的水果，“人”指一类多汁的植物果实，而“死”的自然语言中的意思是“美味”。那么当外星人说出

((苏格拉底➞人)×(人➞死))⇒(苏格拉底➞死)

这个陈述时，实际上是在表达他们对食堂供餐的意见。

 

可以说，形式系统只关心“名（name）”的同一性，即在一次完整的推理中，同一个名字指向的实际意义是相同的。名字的实际意义究竟就是什么，则是由人为赋予的。人们会将形式系统中的变量或常量名映射为他们心中的某种概念。形式系统中的表达式是抽象的，人们对表达式的解释则是具象的。同一个抽象的陈述，可能映射为不同的物理解释；当然，同一个物理意义也以用不同的名字来表示。

 

例如，在上文提到的三段论运算器中，我们只要提供形如(S➞H)和(H➞D)的陈述，它总是能得出形如(S➞D)的结论。如果我们将其中的符号➞换成⊂，那么只要给这台机器提供(S⊂H)和(H⊂D)，它总能得出结论(S⊂D)，虽然我们依然可以宣称此处⊂符号的含义是直觉逻辑中用于表示S特性D的符号，这个运算器是一个三段论运算器，但是显然，对于

 

((S⊂H)×(H⊂D))⇒(S⊂D)

 

更直觉的解释是集合论中的一条运算法则，其中“⊂”是集合论中表示子集关系的符号。

 

除了符号不同，这台机器的运算法则没有任何变化，但是将➞替换为⊂之后，人们直观上会将它当作一台集合论计算器，而不再是三段论计算器。这种符号与意义之间的映射是人为赋予的，把⊂当作集合论计算符号，只是人类长期以来的经验习惯而已。在这个例子里，一套形式系统可以同时映射为两种不同的实际运算，⊂既可以表示三段论，也可以表示集合论；反之，两套不同的符号系统➞和⊂，都可以表示三段论运算。用一句古老的箴言来说，道【可道】，非【常道】；名【可名】，非【常名】。

 

以计算机的基本构成元件——逻辑门为例。一个异或门的输入真值表是

（0，0）➞0

（1，0）➞1

（0，1）➞1

（1，1）➞0

此处1表示布尔运算中的true，0表示false。但是如果把0解释为二进制中的0，1代表二进制中的1，我们会发现这套运算法则恰好与二进制加法的个位运算是一致的。因此，同一个元件既可以表示异或运算，也可以表示加法运算，这取决于我们如何解释符号1与0的含义。加法器就是由这样的门电路组成的。

 

再以数学这一形式系统为例，假设在平行世界的数学中，用#表示加法，用？表示等于，他们会有这样一条加法法则

5?3#2

即我们世界中的

5=3+2

但是在另一个平行世界中，他们把#解释为等于，把?解释为减去，那么这条法则变成了

5-3=2

这其实是一条减法法则。

这个例子可以说明，所有形如a=b+c的加法表达式和形如a-b=c的减法表达式在形式上是一致的。我们完全可以把a=b+c中的+理解为等于，=理解为减去，所有的运算依然是成立的。

 

只要两种运算基本法则的形式完全相同，就可以用同一套形式系统来表示，使用这套系统推演出的一切表达式都可以有两种解释。在这种情况下，我们说这两种运算是同构的。

 

二、什么样的形式能表示逻辑？

形式化的直觉逻辑

——我是阿尔法，我是欧米伽

 

下面我们来讨论一种简单的逻辑系统——直觉逻辑。直觉逻辑有许多不同的表示方式，这里我们采用希尔伯特风格的形式系统。这一系统有两条公理形式，即所有形如

α→β→α （1）

(α→β→γ)→(α→β)→α→γ （2）

 

都是公理。其中每个字母代表一个不可分的元命题，或者一个表达式。该系统唯一的推演规则是，如果α→β和α是定理，那么β也是定理

 

注意此处的定理没有非真即假的概念，证明一个表达式是定理的唯一方式是用公理和推演规则推出它，推出它的否命题为假是无效的，也就是说，这个系统不能使用反证法

 

希尔伯特表达式是右结合的，也就是在表达式的右半部分加括号不影响其含义。公式（1）可以写作

α→(β→α)

也就是说如果α是定理，那么β→α也是定理。公式（2）则可以写作

(α→(β→γ))→((α→β)→(α→γ))

用自然语言来说，如果α能导出β→γ，那么当α能导出β时，α就能导出γ。这个推理过程也是合乎直觉的。

 

用希尔伯特的直觉逻辑公理来做一个小的推理练习，即证明α→α是定理。

Step1. 因为表达式中的符号可以替换，所以我们将公理（2）中的所有γ替换为α，得出

(α→β→α)→(α→β)→α→α（3）是定理。

（因为对于所有α和γ公理（2）都成立，所以当γ=α时，公理（2）显然也成立，这可以看作公理（2）的特例应用）

Step 2. 又因为上式是定理，α→β→α 是公理，根据推演规则，得

(α→β)→α→α是定理

Step3. 再做一次特例应用，将上式中的β替换为β→α，得

(α→β→α)→α→α

Step 4. 最后将因为上式是定理，(α→β→α)是公理，根据推演规则

α→α是定理得证。

 

单个多假设命题=嵌套的单假设命题

——玄生万物，九九归一

 

直觉逻辑有一个重要的推论：如果定理A能导出定理B→C，那么定理A和B能导出定理C，反之亦然。该结论既可以通过公理证明，从直觉上也很容易理解。如果我们给上文中的形式系统上加一个小变化，用×符号来表示两个定理之间的与关系AND，那么该推论可以表示为

 

如果A→B→C是定理，那么A×B→C是定理。

 

该结论可进一步拓展为，如果

A1→A2→A3→……→An→B是定理，那么

A1×A2×A3×……×An→B是定理。

 

这两个表达式在形式系统中等价，多假设的单个命题与单假设的多个嵌套命题是可以互相转化的。

 

引入这个符号之后，直觉逻辑中唯一的推理规则“如果α→β和α是定理，那么β也是定理”可以表示为

 

α×(α→β)→β

 

因此。与之等价的α→((α→β)→β)也是一条定理。有兴趣的话可以运用直觉逻辑的推演规则证明这个结论。

 

命题映射为变量类型

——和其光，同其尘

 

下面我们来给这个推演规则做一次应用，将变量α换作命题A（命题是不可再分的表达式），β换作命题B。如此可以得到一个结论，

如果A→B是定理，A也是定理，那么B就是定理。

 

A×(A→B)→B

 

为了便于称呼，我们给A→B这个定理起名f，表示为f: A→B，意即定理f的内容是命题A→命题B。再给A命名为p，B命名为r。上述表达式变为

 

p:A×(f:A→B)→r:B

 

下面是最重要的一步变换。由于在形式系统中，符号是最不重要的东西，我们将所有的A替换为TypeA，B替换为TypeB，上式依然是命题逻辑唯一的推演规则：

 

p:TypeA×(f:TypeA→TypeB)→r:TypeB

 

下面再把p置换为param，f置换为func，r置换为ret，上述表达式变为

 

param:TypeA×(func:TypeA→TypeB)→ret:TypeB。

 

注意，除了给定理加上名字并且替换相应符号，这个表达式与α×(α→β)→β没有任何本质区别。我们依然可以宣称它代表直觉逻辑唯一的推演规则：如果TypeA是定理，TypeA→TypeB是定理，那么TypeB也是定理，其中的TypeA，TypeB都是命题的名字。但是，对于程序员而言，分明会将它理解为类型系统中唯一的推演规则:

 

如果函数func的入参是类型A，返回值是类型B，那么调用时输入类型为A的变量param，就会得到类型为B的返回值ret。

其中TypeA→TypeB 表示函数func的类型，该函数参数类型为TypeA，返回值类型为TypeB。

 

在这条规则中，加上param和func等等名字只是有助于理解，类型系统的核心规则与命题逻辑的核心规则具有完全一样的形式

 

A×(A→B)→B

 

其中A既可以从程序的角度理解为类型，也可以从逻辑的角度理解为命题，采用不同的解释时，对于这个表达式的解释也会发生相应的变化。

 

这也就是计算机形式化验证的基石——柯里-霍华德同构。它意味着同一套符号系统既可以解释为程序的类型，也可以解释为直觉逻辑的推理。

 

对于多参数的的函数而言，可以将其改造为多个单参数的函数嵌套的形式，再应用以上推演规则。例如：函数

 

fn curry(a:A, b:B) -> C{
　　return foo(a, b);
}
 
curry(x, y)

 

等效于

 

fn curry(a:A) -> B->C {
    let curried = fn(b:B) -> C {
        foo(a, b)
    };
    return curried;
} //curry函数返回一个类型为B->C的函数curried，该函数接受一个类型为B的参数，返回值类型为C
 
let func = curry(x);
func(y);    

这个过程称为柯里化，即如果可以构造类型为A×B→C的函数，那么必然可以构造类型为A→(B→C)的函数。注意看前一节 单个多假设命题=嵌套的单假设命题 中，直觉逻辑的推论，即

 

如果可以推出定理A→(B→C)，那么可以推出定理 A×B→C

 

这个过程与程序的柯里化过程是同构的。

 

证明映射为程序

——色不异空，空不异色；色即是空，空即是色

 

对于一个程序员而言，如果他能构造一个类型为A->B的函数，则表示可以构造一个定理A->B证明，其中A是假设，B是结论。函数体从参数到返回值的步骤，等同于证明从假设到结论的步骤。如果这个函数能够通过编译器检验而无类型错误，则说明对应的证明是没有逻辑谬误的。

 

换句话说，每一个直觉逻辑表达式都可以映射为一个函数的类型，每一个可证明的直觉逻辑表达式都可以映射为一个可以实现的函数类型。

 

在更详细地解释这两套推演系统是如何对应之前，先看一张表：

 

变量名：变量类型	命题名：元命题
函数名：函数类型	定理名：定理内容
参数名：参数类型	假设名：假设内容
返回名：返回类型	结论名：结论内容
函数体	证明（proof）
类型检查(type checker)	证明验证(proof verifier)
库函数	已证明的定理
函数调用	定理应用
构造函数	公理
类型推导	命题推演
类型错误	逻辑谬误
……	……

 

这张表可以列得很长很长，直到我们为计算机程序中的每一个概念在直觉逻辑中找到一个对应物。甚至包括一些边缘概念

缘于递归的栈溢出	缘于自引用的悖论
停机问题	哥德尔不完备

下面用例子来说明一下表中某些项的对应关系。

 

例一：证明的验证

假设有这样一段代码：

struct A {
    String field;
}
 
impl A {
    fn new(field: String) -> A {
        A { field }
    }
}
 
 
fn string_implies_A(field: String) -> A {
    A::new(field)
}
 
let hypothesis: String = String::new();
let conclusion: A = string_implies_A(hypothesis);    

这个程序的结构如图

 

 

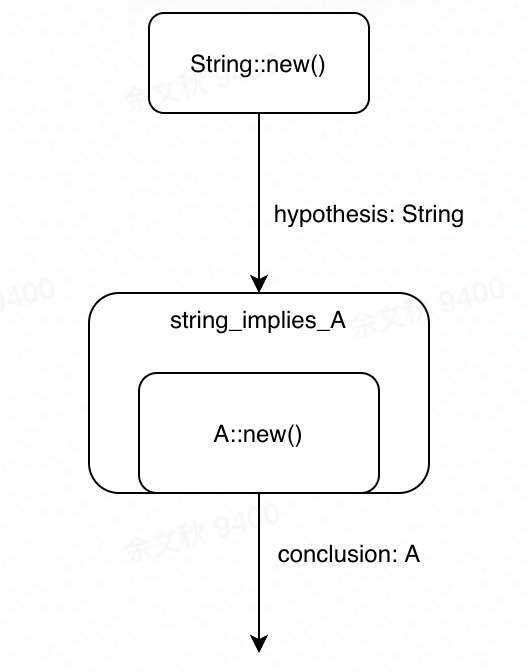
可以看到它的核心结构是重命名了A::new()为string_implies_A，输入一个类型为String的参数hypothesis，返回conclusion:A。

 

我们写好这样一段程序，交给编译器，从编译器的角度很好理解

• string_implies_A重命名了函数A::new(),类型是String->A；
• 输入的变量hypothesis，类型String与string_implies_A的参数匹配，该变量用String::new（）初始化。
• 调用string_implies_A返回值类型为A，与conclusion预定义的类型相同。

编译器会告诉我们这段代码的类型推导过程是完全正确的。

 

但是从逻辑的角度，这个过程就变成我们写好了这样一段证明，交给证明器。尽管机器工作的过程完全相同，对各个符号的人为理解却完全不同。

• 首先，string_implies_A重命名了公理A::new()，内容是String->A；
• 其次，输入条件hypothesis，内容String与string_implies_A的假设匹配，String:new()表示hypothesis来自公理。
• 应用定理string_implies_A返回A，与预设conclusion的内容A相同。

证明器会告诉我们这段证明的命题推理过程是完全正确的。

 

上述程序/证明的核心是string_implies_A。在两种理解中，string_implies_A的类型String->A，既可以理解为函数string_implies_A接受参数String，返回参数A，也可以理解为定理接受假设String，返回结论A。

函数调用输入参数的过程就是定理接收假设条件的过程。在计算机中，所有的程序都可以看作函数的组合，一个函数的返回值会用作另一个函数的参数，得到下一步返回值。在逻辑系统中，所有的证明也都可以看作定理的组合，一个定理的结论可以作为另一个定理的条件，得出新的结论。

 

当程序无法通过类型校验时，表明相应的证明也无法通过验证。例如，将函数主体改为

let hypothesis: String;
let conclusion: A = string_implies_A(hypothesis);

编译器会告诉我们hypothesis没有使用String::new()初始化，放在证明中，这相当于我们在证明中定义假设hypothesis：String时，没有使用String::new()，即String是公理这一条件。在用自然语言写成的非形式化证明中，这类对隐式假设的忽略是常见的谬误，在写程序时，忘记初始化也是常见的谬误，但编译器永远不会漏掉这样的问题。

 

再比如，将函数主体改为

let hypothesis: Double = Double::new();
let conclusion: A = string_implies_A(hypothesis);

编译器会告诉我们hypothesis的类型与函数string_implies_A不匹配。从证明的角度来解释，这相当于我们在证明中使用了公理Double，而定理string_implies_A的假设是String，Double不能作为使用该定理的条件。

 

例二：计算机推理

再来看看这样一段代码

use lib_fun::string_implies_A;
 
let hypothesis: String = String::new();
let conclusion = string_implies_A(hypothesis);

与例一相比，这个程序主要有两个变化。一是string_implies_A不是由自己定义，而是引入的库函数；二是conclusion没有显式地声明类型，而是由编译器进行类型推导。

 

先来看库函数如何从两种角度来解释。在use lib_fun::string_implies_A中，库函数string_implies_A代表已通过编译，可以直接调用的函数，我们不必关心它的实现细节，编译器会确保它的类型String -> A是可以通过类型校验的。

 

从证明器的角度看来，string_implies_A代表已通过验证，可以直接应用的定理。我们不必关心它的证明细节，证明器确保它所证明的定理String -> A是可以通过证明器检验的。

 

再来看类型推导如何从两种角度来解释。在let conclusion = string_implies_A(hypothesis)中，将类型为String -> A的函数string_implies_A应用于变量hypothesis: String，编译器可以推导出conclusion的类型必然是A。用在证明里，相当于将定理String -> A应用于假设hypothesis：String，可以得出结论conclusion必然为A。

 

如果加一点变化，删去hypothesis的定义，加上conclusion的类型

use lib_fun::string_implies_A;
 
let conclusion：A = string_implies_A(hypothesis);

编译器会告诉我们缺少一个类型为String的变量hypothesis。开发者就会知道调用其它函数获得这个变量，或者尝试直接使用构造函数String::new()。

从证明器的角度来解释，这意味着当我们想要利用String->A证明A时，证明器告诉我们缺少一个条件hypothesis: String。我们可以利用其它定理推导出String，或者使用公理String。

 

例三：计算机辅助证明

假设我们想证明前文所述的定理f：A×(A→B)→B，根据柯里-霍华德同构，这意味着我们想要构造一个类型为A×(A->B)->B的函数。我们可以一步到位，手动写出这个函数

fn f(a:A, h:A->B) -> B {
    return h(a)
}

编译器会告诉我们这个函数可以通过类型校验，意即证明器告诉我们这个证明是正确的。

 

如果我们试图证明表达式A×(B→A)→B，会发现利用现有的函数和变量，无法构造类型为A×(B→A)→B的函数，这意味着这个表达式是推导不出来的。

 

在大型数理逻辑问题中，如果我们想要证明的表达式过于复杂，人工构造函数的难度会以指数曲线上升，这时可以借助计算机的类型推导工具。

 

还是以A×(A→B)→B为例。

程序角度：

• 直接将这个类型输入计算机，编译器会分析出这一个函数，函数接受a: A和h: A->B两个参数，返回B；
• 尝试在代码的最后一行调用其中一个参数h，即类型为A->B的函数，编译器告诉我们，给这个函数输入类型为A的参数就可以返回B；
• 将另一个参数a输入该函数h，类型为A×(A→B)→B的函数构造完成。

 

证明角度：

• 直接将这个表达式输入计算机，证明器会分析出这一个定理，定理接受a: A和h: A->B两个假设，结论B；
• 尝试在代码的最后一步应用内容为A->B的定理h，证明器告诉我们，输入内容为A的假设就可以得到B；
• 最后将a输入该定理h，内容为A×(A→B)→B的定理得证。

 

如今的编译器可以自动做一些类型推导，但是对于过于复杂的程序结构，还是需要手动在关键节点显式指定表达式的类型；同理，证明器可以做部分自动推理，辅助人类构造证明，并验证证明的正确性，而不是完全代替人类自动证明。计算机辅助证明工具Coq正是这样工作的。

 

在以上所有例子中，type checker只是按照A×(A→B)→B这样预设的法则运行，要将符号A解释为程序的类型还是证明中的命题取决于人脑中的概念。对计算机而言，这些符号本身是没有意义的，可以任意替换为TypeA，Apple等等。正如三段论中“苏格拉底”的本质，也只是四个没有任何意义的汉字符号，而不是某位伟大的哲学家其人。意义不在符号里，不在三极管与电流之中，在乎人心本身。

 

佛告须菩提：“凡所有相，皆是虚妄；若见诸相非相，即见如来。” ——《金刚经》

 

三、形式可以表示什么样的逻辑？

低阶逻辑衍生为高阶逻辑

——道生一，一生二，二生三，三生万物

 

柯里-霍华德同构表明，在直觉逻辑中，所有用形式化的方法写成的证明，都可以解释为一个带类型的程序，并交给计算机验证。类型错误意味着这个证明缺乏某个条件，或条件与假设不匹配。

 

然而，直觉逻辑的表达能力毕竟是有限的。例如，由于没有“真”“假”的定义，直觉逻辑无法使用反证法，我们只能推出一个定理，而不能证明某个命题的否命题为假。但是，利用直觉逻辑的符号定义新的概念，引入新的公理，可以增加直觉逻辑的表达能力。

 

高阶逻辑中新引入的概念，可以由低阶逻辑中已有的法则来定义。由于篇幅所限，不能对形式逻辑的具体定义展开讨论，这里依然用数学来类比。古老的四则运算系统仅包含+ - * /和（）=七个符号以及它们的运算法则，这一系统的表达能力是有限的，无法用来表示 已知正方形的面积，求其边长 这样的运算。

 

为了解决这一问题，数学家以乘法为基础定义了幂运算，m的n次幂等于n个m相乘的结果。接着，数学家将幂运算的逆运算定义为开方运算，用符号√ 来表示，如此就能表示 求特定面积的正方形边长 这样的计算过程了。

 

随着数学的发展，越来越多的符号和运算被发明出来，如积分，求和，阶乘，等等等等，然而新符号总是有限的，不同数学家采用的符号也不尽相同，新的数学问题却源源不断地涌现出来，因此，亟需一种统一的，强大的符号系统，用于表示尽可能多的数学运算。

 

上个世纪前半叶，许多数学家与计算学家都投入了这项工作，如图灵设计的图灵机，丘奇设计的λ演算等等。需要注意的是，虽然图灵机的描述使之听起来很像一台用物理器件造出的机器，但它的本质是一个抽象的计算模型，所谓纸带、读写头等等，都是用来定义运算规则的符号。图灵机可以有各种各样的实现，我们可以用纸笔来执行图灵机的运算过程，也可以尝试用机械元件来制造一个自动运行的图灵机（但图灵没造出来）；就像布尔运算是一个抽象的计算模型，我们既可以用三极管来实现它，也可以用秦始皇的人列方阵一样。

 

所有可以用图灵机来表示的问题称为（图灵）可计算的。丘奇证明他的λ演算和图灵机等价，因此，λ演算是图灵完备的。它们都是现有最强的计算模型，可以计算所有可计算问题。

 

回到逻辑系统，直觉逻辑是最简单的逻辑系统。在直觉逻辑的基础上定义True，False两个符号和非运算法则，就得到了一个表达能力更强的系统，我们称之为命题逻辑。在命题逻辑中，证明一个定理的方法不只有推出它，还可以通过证明它的否命题为假来实现。

 

在命题逻辑的基础上引入量词符号存在∃，所有∀，就得到了一阶逻辑。在一阶逻辑中，可以写出如下表达式：

((苏格拉底➞人)×(∀人➞死)) (1)

((苏格拉底➞人)×(∃人➞死)) (2)

 

表达式（1）可以推出苏格拉底会死，表达式（2）无法推出苏格拉底会死，在初级的直觉逻辑中，这两种计算式的区别是无法体现的。

 

在一阶逻辑中，引入“域”的概念，则可以得到二阶逻辑。在二阶逻辑之上，还有高阶逻辑，类型论等等等等。

 

低阶逻辑中引入新的符号与推理法则，可以得到更强的逻辑系统；相应地，在表示直觉逻辑的计算机语言中，定义新的符号与函数，可以得到更强大的证明器，用于表示和证明更复杂的定理。例如，我们可以定义0，1，2，3等自然数符号，+等计算符号，再将加法运算法则，即皮亚诺引理编码为公理。如此，就能利用证明器进行数学推导与证明了。计算机辅助证明工具Coq本身提供了很多已证明的数学定理作为库函数，可以直接引用以辅助证明。

 

形而下者谓之器 形而上者谓之道

 十七世纪，费马一拍脑袋写了个猜想，顺手批注说自己有个绝妙证明，可惜纸太小写不下。

三百多年后，Andrew Wiles才以108页的论文证明了费马的大定理，又花了两年时间与审稿人一起发现并解决了证明中的所有漏洞。

 

所有人都相信费马大定理是正确的，因为人们相信Wiles和他的审稿人作为数学家的专业能力。虽然大部分人穷其一生都读不懂Wiles的证明。

 

可数学家毕竟是人，是人就会犯错误。1991年，菲尔兹奖得主Vladimir Voevodsky发表了对某个命题的证明，1998年，数学家Carlos Simpson 发表了关于该命题的一个反例，却没有提出原论文证明中的漏洞。Voevodsky无法确证是证明出了错还是反例出了错，或是两个人对某个概念的理解有微妙的偏差，数学界也不知道，他们只是默默地不再引用原论文了。类似这样的事故促使Voevodsky决心投身形式化证明的研究，因为——

 

人们应当信任统一的，严格的，形式化的数学，而不是信任数学家。

 

形式化证明的好处是显而易见的：

• 一般人不可能读懂108页的费马大定理证明，但是机器可以阅读成千上万行形式化的证明。
• 一般人引用费马大定理时，必须信任Wiles和他的审稿人；如果费马大定理被形式化地证明了，就只需要信任prover，同时也是type checker——一个一般化地，被全世界专业人士反复检验的工具。
• 一般人验证每一个自然语言写成的证明时，都要一行一行地读懂它的证明，引理，引理的证明，等等等等。对于形式化的验证，则只需要检验同一个type checker的正确性。它的推理规则相较于费马大定理证明所包含的所有推理是极简洁的。
• Type checker在一定程度上可以自动推理，例如，著名的四色问题就是使用计算机辅助证明解决的。

 

如今，数学证明的形式化表达对于人类而言，还是过于繁琐和晦涩，就如同过去的程序员所面对的纸带和汇编一样。也许有一天，形式化的证明也会被高度抽象，更加接近于自然语言，就像从机器码到高级语言的发展历程一样。那时的Prover将会结合神经网络成为新一代AI，一种既遵循大量经验，也会依赖严格的、合乎逻辑的推理而产生新概念的智能，一台思考机器。

 

 

思考题：
每一个形式化的证明都可以解释为一个带类型的程序。那么反过来，每一个程序都可以解释成一个证明吗？Hello World证明了什么？