X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0!
其中, a[i]为整数,并且0 <= a[i] <= i, 0 <= i < n, 表示当前未出现的的元素中排第几个,这就是康托展开。
例如有3个数(1,2,3),则其排列组合及其相应的康托展开值如下:
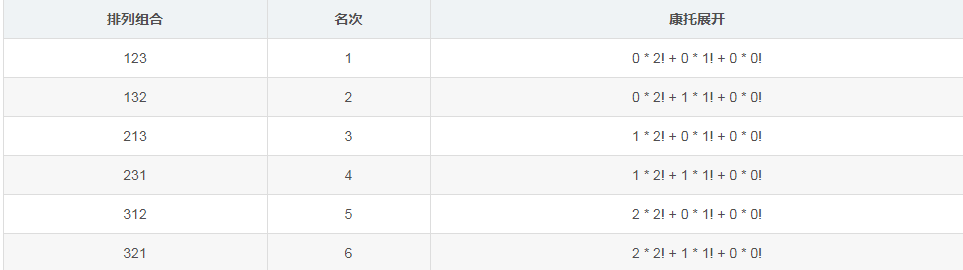
比如其中的 231:
想要计算排在它前面的排列组合数目(123,132,213),则可以转化为计算比首位小即小于2的所有排列「1 * 2!」,首位相等为2并且第二位小于3的所有排列「1 * 1!」,前两位相等为23并且第三位小于1的所有排列(0 * 0!)的和即可,康托展开为:1 * 2!+1 * 1+0 * 0=3。
所以小于231的组合有3个,所以231的名次是4。
(为了理解自己加的例子,不是原文内容)再比如312:比3小的有1、2所以是2*2!;再看1,没有比1小的,所以是0*1!;最后看2,比2小的只有1,但1在前面已经用过了,所以为0*0!.
————————————————
版权声明:本文为CSDN博主「wbin233」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/wbin233/article/details/72998375
公式:



