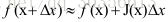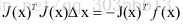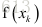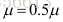一起学ORBSLAM2（7）ORBSLAM中的优化问题

转载请注明原创地址：https://blog.csdn.net/qq_30356613/article/category/6897125

ORBSLAM是一种基于优化方法的SLAM方法，与之前的基于滤波器方法有很大的不同，工程中引入了第三方库g2o，g2o是基于图优化的优化算法库。

首先了解什么是图优化，图优化是将普通的优化问题用图的方式(变量用节点表示，关系用边来表示)来表示（参考文章：g2o: A general Framework for Graph Optimization），如下最小二乘问题表达式可以表示为：

，其中为误差函数，为信息矩阵

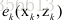
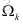
求解该最小二乘问题，有多种方法，最常用的也是g2o中用到的两种方法分别为：高斯牛顿法和莱温伯格-马夸尔特。

高斯牛顿法将误差函数通过泰勒展开为多项式形式，如下：

主要思想是将泰勒展开为： 

其中，为关于x的导数，实际上是一个雅可比矩阵。为了使得达到最小值，我们需要求解一个线性最小二乘问题：

                                  （式2.16）

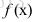
展开上式对上式关于求导得到

 

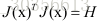
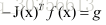
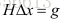
令，得到：

                                                    （式2.17）

求解该线性方程可以解出的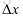值。

算法步骤总结为：

（1）给定初始值x0

（2）对于第k次迭代，求出当前的雅可比矩阵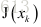和误差

（3）求解增量方程：

（4）若足够小，则停止。否则，令，返回（2）^[1]

 

Levenberg-Marquart梯度下降法如下：

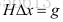
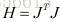
上节中我们介绍的高斯牛顿法存在其缺陷，比如说在求解增量方程时，要求H是正定的，而只能符合半正定型。也就是说H的奇异性会使得增量的稳定性变差，从而可能导致算法的不收敛性，因此我们提出了另一种改进方法Levenberg-Marquart梯度下降法。

其主要算法思想是在原来的基础上给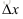加上一个信赖区域，使得在信赖区域里边算法是有效的，否则无效。算法流程如下：

（1）给定初始值x0，以及初始优化半径

（2）对于第k次迭代，求解

这里的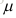是信赖区域的半径，D将在后文中说明

（3）计算

（4）若，则

（5）若，则

（6）如果大于某阈值，认为近似可行，令

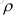
（7）判断算法是否收敛。如不收敛则返回2，否则结束^[1]。

上述为标准算法，我们在使用其解决最小二乘问题时为了满足系统的鲁棒性，我们通常将最小二乘用鲁棒核函数来包装，以避免在有错误数据时使系统专注于调整一个错误的值（二范数的增长速度太快），因此我们将最小二乘问题变为如下的形式：

原最小二乘问题：

 

将其用Huber核函数包装：

 

用wk对误差函数e进一步加权

 

最终的最小二乘函数变为：

 

上述过程使得最小二乘问题的解决方案更具有鲁棒性。

在上述两个梯度下降法中最重要的是雅可比矩阵的计算以及大型线性方程的求解，这两块具体问题需要具体分析，我们以SLAM中的地图点和帧位姿同时优化问题为例来讲解其求解过程：

一般情况下一个三维空间中的点经过下述过程映射到像素坐标：

，其中K是相机内参数矩阵，为当前相机位姿，为地图点坐标。

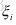
误差函数可以写为：

则最小二乘问题可以用下式进行描述：

（1）

此最小二乘的变量为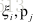：，同一用x描述，

令，我们得到上式函数（1）关于变量的雅可比矩阵为：

令

则雅克比矩阵为：

对于和我们有：

其中为误差关于李代数的偏导数，其求解方法如下：

          

     （式4.2）

根据2.1.2节中的李代数求导模型式2.8得到：

                                      （式4.3）

整理式4.1、式4.2、式4.3得到最终的结果：

       （式4.4）

为误差对于坐标点的偏导数，其求解方法如下：

 

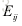
第一项根据式4.2可以得到，第二式中

，因此在求导之后导数为R

                                （式4.5）

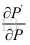
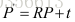
然后我们就可以根据雅克比矩阵进行求解了，其中对于大型的BA优化我们通常用吴消元法进行求解线性方程。吴消元法的相关知识参考高翔SLAM14讲第10章10.2.3 P249.

ORB-SLAM2中用到优化的情况分为以下几种：

1. 优化位姿欧式变换矩阵T（tracking线程）

2. 优化位姿相似变换矩阵S（回环检测）

3. 局部BA优化（tracking线程）

4. 优化全局位姿（回环检测）

5. 同步优化全局位姿和地图点（回环检测）

分别简要介绍：

1. 优化位姿欧式变换矩阵T（tracking线程）

优化目标是单帧相机位姿

1> 设置优化器算法

2> 将变量作为节点（当前待优化帧的初始位姿）添加进入图优化

3> 添加边将地图点和待优化帧的位姿连接，每一个地图点对应一条边。

4> 开始迭代优化，每次迭代下降10次，然后根据当前优化结果位姿筛选内点，用内点重新进行迭代下降优化，依次循环4次，得到最终结果。

 

2. 优化位姿相似变换矩阵S（回环检测）

优化目标是两关键帧之间的相似变换矩阵

1> 设置优化器算法

2> 将变量（当前待优化帧的初始位姿）作为非固定节点添加进入图优化

3> 将变量（两关键帧的地图点）作为固定节点添加进入图优化

4> 添加边将两关键帧地图点和待优化帧的位姿连接，每一个位姿对应两条边，从关键帧1像素坐标映射到关键帧2像素坐标，从关键帧2像素坐标映射到关键帧1像素坐标。

5> 开始迭代优化，迭代下降5次，然后根据当前优化结果位姿筛选内点，用内点重新进行迭代下降优化，优化结果为计算得到的两关键帧之间的相似变换矩阵。

 

3. 局部BA优化（tracking线程）

优化目标是待优化关键帧及其共视关键帧

1> 设置优化器算法

2> 将变量（当前关键帧及其共视关键帧的初始位姿）作为非固定（初始帧固定）节点添加进入图优化

2> 将变量（观察到当前关键帧及其共视关键帧中地图点的关键帧初始位姿）作为固定节点添加进入图优化

3> 将变量（当前关键帧及其共视关键帧的地图点）作为非固定节点添加进入图优化

4> 添加边将关键帧共视图中地图点和该地图点的观察帧的位姿连接。

5> 开始迭代优化，迭代下降5次，然后根据当前优化结果位姿筛选内点，用内点重新进行迭代下降优化。

6> 恢复优化后的各关键帧位姿和关键帧地图点。

 

4. 优化全局位姿（回环检测）

优化目标是整个地图中关键帧的位姿

1> 设置优化器算法

2> 将变量（当前全局地图中所有关键帧的初始位姿（相似变换矩阵））作为非固定（非回环帧）节点添加进入图优化

3> 添加回环边将回环中始端和末端的位姿连接。

4> 添加三种普通边（1>父节点边  2> 回环边(此回环边与3中的回环边不同在于:包括历史检测到的回环边)  3> 共视边   (位姿用矫正的相似变换矩阵)）

5> 开始迭代优化，迭代下降20次。

6> 恢复优化后的各关键帧位姿。

 

5. 同步优化全局位姿和地图点（回环检测）

优化目标是整个地图的关键帧位姿和地图点3D坐标

1> 设置优化器算法

2> 将变量（当前全局地图中所有关键帧的初始位姿和地图点的3D坐标）作为非固定（非初始帧）节点添加进入图优化

3> 添加边将关键帧位姿和地图点坐标连接。

5> 开始迭代优化，迭代下降20次。

6> 恢复优化后的各关键帧位姿和地图点坐标。