变分推断

• http://cairohy.github.io/2018/02/28/vi/VI-1/
• https://zhuanlan.zhihu.com/p/49401976

一、近似推断问题

马尔科夫蒙特卡洛（MCMC）采样是近似推断（Approximate Inference）的一种重要方法，其改进包括Metropolis-Hastings算法，Gibbs采样。

在MCMC不满足性能要求的时候，我们使用变分推断（Variational Inference，VI）。变分推断通过优化逼近后验，而MCMC通过采样逼近后验。

对观测数据\(x = (x_1,\ldots,x_n)\)和隐变量\(z = (z_1,\ldots,z_m)\),推断问题（inference）希望计算出隐变量的后验概率\(p(z|x)\)，利用贝叶斯公式重写后验概率如下公式。在确定隐变量z的先验概率\(p(z)\)时，公式中的联合概率\(p(z,x)\)能够计算，而\(p(x)\)需要积分\(p(x) = \int p(z,x) dz\)计算，但是通常，这个积分没有解析解，利用采样的方法计算效率也非常低。

\[p(z|x) =\frac{p(z,x)}{p(x)} \]

二、变分分布和ELBO

变分推断选择一类分布族Q（称为变分分布族），将推断问题转换为优化\(q^*\in Q\)使得与后验\(p(z|x)\)的差别最小。

\[q^*(z) = argmin_{q(z)\in Q } KL[q(z)||p(z|x)] \]

变分推断使用\(KL[q||p]\)衡量变分分布（即分布q）和真实后验p之间的差别，KL散度是非对称的，这种形式的KL着重于惩罚真实后验p很小时变分概率q很大的情况。

我们无法最小化目标函数\(KL[q||p]\)，因为KL中包含有\(log⁡p(x)\)，如下推导：

\[\begin{aligned} KL[q(z)||p(z|x)] &= E_{q(z)}[\log q(z)] - E_{q(z)}[\log p(z|x)]\\ &=E_{q(z)}[\log q(z)] - E_{q(z)}[\log p(z,x)]+E_{q(z)}[\log p(x)]\\ &=E_{q(z)}[\log q(z)] - E_{q(z)}[\log p(z,x)]+\log p(x) \end{aligned} \]

但是，通过上面公式的变化可以得到一个新的目标函数ELBO：

\[\begin{aligned} ELBO(q) &= \log p(x) - KL[q(z)||p(z|x)] \\ &= E_{q(z)}[\log p(z,x)] - E_{q(z)}[\log q(z)] \end{aligned} \]

这个目标函数可以从两个方面来解释：

• 由于\(log⁡p(x)\)相对于\(q(z)\)是一个常量，而我们想要最小化KL，\(ELBO\)等于负的KL加上一个常量，所以我们最大化\(ELBO\)就等价于最小化KL。
• 最大化\(log⁡p(x)\)就是对观测数据的极大似然估计（即log evidence），由于KL是非负的，所以这个目标函数是极大似然估计的下确界（即evidence lower bound, ELBO）。

继续推导：

\[\begin{aligned} ELBO(q) &= E_{q(z)}[\log p(z,x)] - E_{q(z)}[\log q(z)]\\ &=E_{q(z)}[\log (p(x|z)p(z))]- E_{q(z)}[\log q(z)]\\ &=E_{q(z)}[\log p(x|z)] + E_{q(z)}[\log p(z)] - E_{q(z)}[\log q(z)]\\ &= E_{q(z)}[\log p(x|z)] - KL[q(z)||p(z)] \end{aligned} \]

从结果来看，\(ELBO\)目标函数第一项是似然的期望，第二项是与先验之间的差别。所以最大化ELBO就是在（1）隐变量对观测数据的解释最佳和（2）变分分布q更靠近先验之间平衡。

三、平均场变分分布族

对变分推断中选择的变分分布族Q进行介绍。

由于分布族Q越复杂，变分推断的优化就越复杂。一般变分推断中会假定一个性质，就是选择的分布族是平均场变分分布族（mean-field variational family）。这个性质保证了每一个隐变量\(z_j\)都相互独立而且只受自己的分布\(q_j\)的参数影响（即满足\(q(z) = \prod_j q_j(z_j)\))）。如果隐变量互相有影响，那么这种变分推断被称为结构化变分推断。

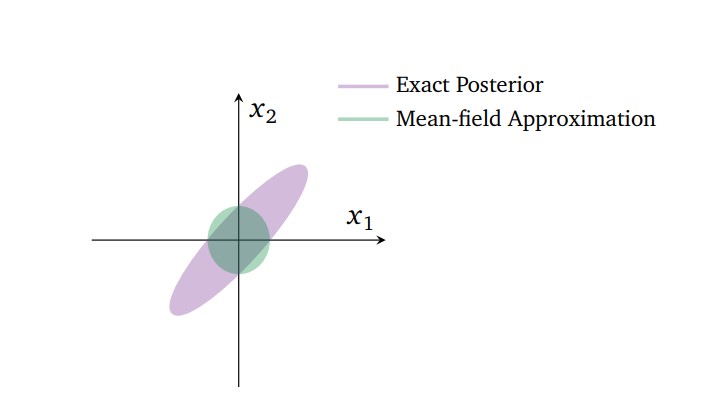
使用平均场变分分布族的缺点是，当隐变量之间互相有关联的时候（性质被破坏）逼近的效果就会下降。比如下图的二维高斯后验，\(x_1\)和\(x_2\)两个隐变量的后验概率是紫色的椭圆形部分，而我们使用mean-field approximation的时候，会学习到一个均值相同但协方差不同的二维高斯分布。

四、优化

针对平均场变分分布，坐标上升近似推断算法（CAVI）是最常见的优化方法。CAVI交替地更新每个隐变量，更新时固定其他的隐变量的变分分布参数，用来计算当前隐变量zj的坐标上升公式。CAVI的算法步骤如下图所示。

首先，我们计算最佳分布\(q_j\)的表达式：

\[\begin{aligned} q&=E[p(\cdot)]\\ &=exp\{\log E[p(\cdot)]\}\\ &\approx exp\{ \log [E(p(\cdot)] - Var(p(\cdot))/(2*E[p(\cdot)]^2)\}\\ &= exp\{\log (E[p(\cdot)]\} * exp\{ h(p(\cdot)) \}\\ &< exp\{\log (E[p(\cdot)]\} \end{aligned} \]

因为在二阶泰勒展开的条件下\(q= exp\{\log (E[p(\cdot)]\} * exp\{ h(p(\cdot)) \}\\\)，且\(q^*_j(z_j)=E[p(z_j|z_{-j},x)]\)，故\(q_j\)与对数条件概率期望的指数成比例：

\[q^*_j(z_j)\propto exp\{E_{-j}[\log p(z_j|z_{-j},x)]\} \]

由于隐变量之间独立，这个公式右侧的期望项可以转化为：

\[\begin{aligned} E_{-j}[\log p(z_j|z_{-j},x)] &= E_{-j}[\log \frac {p(z_j,z_{-j}|x)}{p(z_{-j})}]\\ &=E_{-j}[\log p(z_j,z_{-j}|x)] - E_{-j}[\log p(z_{-j})]\\ &=E_{-j}[\log p(z_j,z_{-j},x)] - E_{-j}[\log p(z_{-j})]- E_{-j}[\log p(x)]\\ &=E_{-j}[\log p(z_j,z_{-j},x)] - const. \end{aligned} \]

因此，我们得到如下结论，也就是知道了联合分布的对数期望（而由于其他的隐变量确定，联合概率可求），就可以求最佳变分分布\(q^*_j\)：

\[\begin{aligned} q^*_j(z_j)&\propto exp\{E_{-j}[\log p(z_j,z_{-j},x)] - const.\} \\ q^*_j(z_j)&\propto exp\{E_{-j}[\log p(z_j,z_{-j},x)]\} \\ \end{aligned} \]

在平均场变分分布族的假设下，\(ELBO\)可以被分解为对每一个隐变量\(z_j\)的函数。根据隐变量分解后的\(ELBO\)中，利用\(q\)分布的平均场性质，第一项将联合概率的期望迭代求出，第二项分解了变分分布的期望。当我们最大化\(q_j\)时，也就最大化了分解后的\(ELBO\)。