【R统计】基于欧几里得距离进行的聚类分析

题目：

为了深入地了解我国人口的文化程度，利用1990年全国普查数据对全国30个省、直辖市、自治区进行聚类分析，分别选用了三个指标：（1）大学以上文化程度的人口占全部人口的比例（DXBZ）；（2）初中文化程度的人口占全部人口的比例（CZBZ）；（3）文盲半文盲人口占全部人口的比例（WMBZ）分别用来反映较高、中等、较低文化程度人口的状况。（1）计算样本的欧几里得距离，分别用最长距离法、均值法、重心法和ward法作聚类分析，并画出相应的谱系图，如果将所有样本分为4类，试写出个种方案的分类结果；（2）用动态聚类方法（共分为4类），给出相应的分类结果。

数据：

地区	DXBZ	CZBZ	WMBZ
北京	9.30	30.55	8.70
天津	4.67	29.38	8.92
河北	0.96	24.69	15.21
山西	1.38	29.24	11.30
内蒙古	1.48	25.47	15.39
辽宁	2.60	32.32	8.81
吉林	2.15	26.31	10.49
黑龙江	2.14	28.46	10.87
上海	6.53	31.59	11.04
江苏	1.47	26.43	17.23
浙江	1.17	23.74	17.46
安徽	0.88	19.97	24.43
福建	1.23	16.87	15.63
江西	0.99	18.84	16.22
山东	0.98	25.18	16.87
河南	0.85	26.55	16.15
湖北	1.57	23.16	15.79
湖南	1.14	22.57	12.10
广东	1.34	23.04	10.45
广西	0.79	19.14	10.61
海南	1.24	22.53	13.97
四川	0.96	21.65	16.24
贵州	0.78	14.65	24.27
云南	0.81	13.85	25.44
西藏	0.57	3.85	44.43
陕西	1.67	24.36	17.62
甘肃	1.10	16.85	27.93
青海	1.49	17.76	27.70
宁夏	1.61	20.27	22.06
新疆	1.85	20.66	12.75

　　

脚本：

#原始数据
X<-data.frame(
   DXBZ=c(9.30, 4.67, 0.96, 1.38, 1.48, 2.60, 2.15, 2.14, 6.53, 1.47, 
          1.17, 0.88, 1.23, 0.99, 0.98, 0.85, 1.57, 1.14, 1.34, 0.79, 
          1.24, 0.96, 0.78, 0.81, 0.57, 1.67, 1.10, 1.49, 1.61, 1.85),
   CZBZ=c(30.55, 29.38, 24.69, 29.24, 25.47, 32.32, 26.31, 28.46,
          31.59, 26.43, 23.74, 19.97, 16.87, 18.84, 25.18, 26.55, 
          23.16, 22.57, 23.04, 19.14, 22.53, 21.65, 14.65, 13.85, 
           3.85, 24.36, 16.85, 17.76, 20.27, 20.66),          
   WMBZ=c( 8.70,  8.92, 15.21, 11.30, 15.39,  8.81, 10.49, 10.87, 
          11.04, 17.23, 17.46, 24.43, 15.63, 16.22, 16.87, 16.15, 
          15.79, 12.10, 10.45, 10.61, 13.97, 16.24, 24.27, 25.44, 
          44.43, 17.62, 27.93, 27.70, 22.06, 12.75),
   row.names = c("北京", "天津", "河北", "山西", "内蒙古", "辽宁", "吉林", 
                   "黑龙江", "上海", "江苏", "浙江", "安徽", "福建", "江西", 
                   "山东",  "河南", "湖北", "湖南", "广东", "广西", "海南", 
                   "四川", "贵州", "云南", "西藏", "陕西", "甘肃", "青海", 
                   "宁夏", "新疆")
)

#计算
Province<-dist(X) #计算欧几里得距离
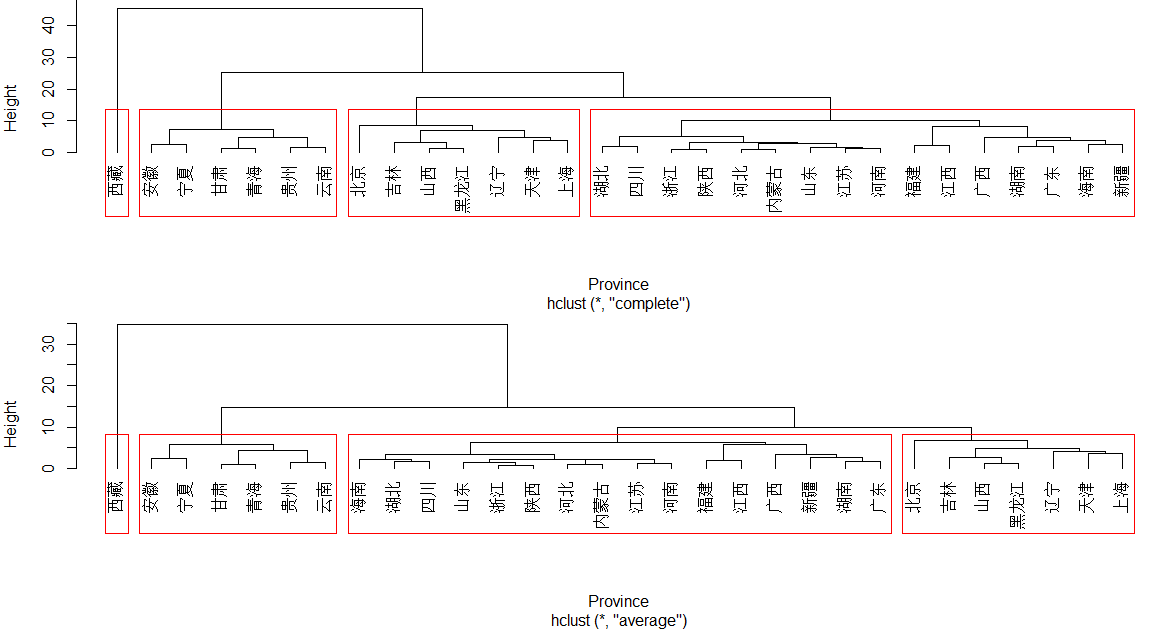
hc1<-hclust(Province, "complete") #最长距离法
hc2<-hclust(Province, "average") #均值法
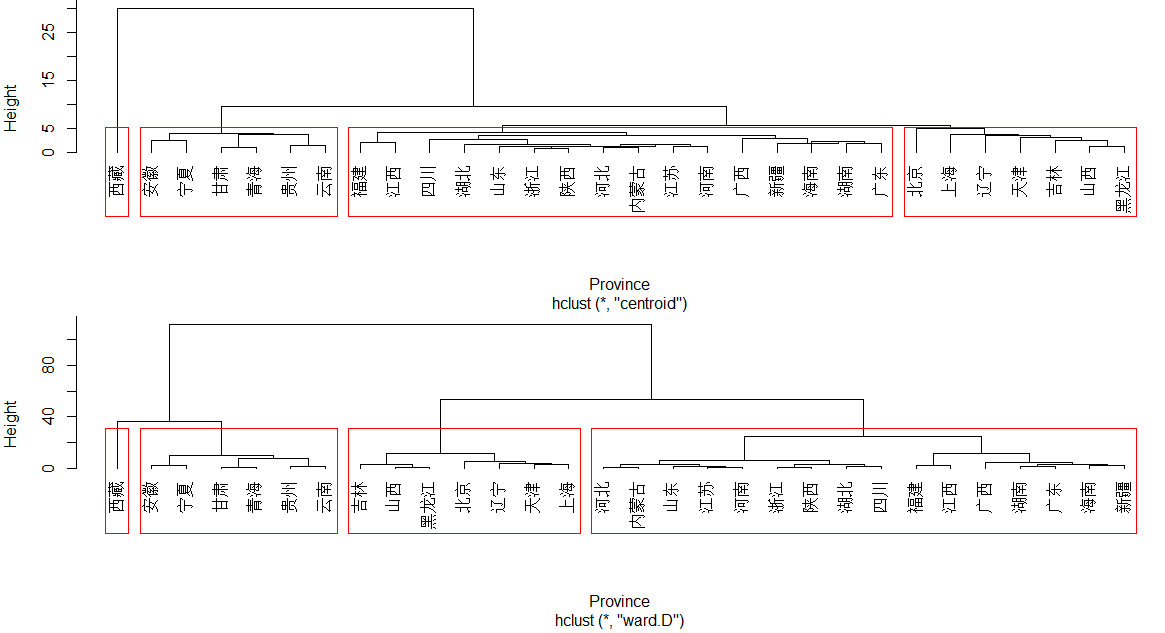
hc3<-hclust(Province, "centroid") #重心法
hc4<-hclust(Province, "ward") #Ward法

#输出图1
opar<-par(mfrow=c(2,1), mar=c(5.2,4,0,0))
plclust(hc1,hang=-1)
re1<-rect.hclust(hc1,k=4,border="red")
plclust(hc2,hang=-1)
re2<-rect.hclust(hc2,k=4,border="red")
par(opar)

#输出图2
opar<-par(mfrow=c(2,1), mar=c(5.2,4,0,0))
plclust(hc3,hang=-1)
re3<-rect.hclust(hc3,k=4,border="red")
plclust(hc4,hang=-1)
re4<-rect.hclust(hc4,k=4,border="red")
par(opar)


km<-kmeans(X, centers=4); 
sort(km$cluster) #排序便于输出
##输出如下##
#河北 内蒙古   江苏   浙江   福建   江西   山东   河南   湖北   湖南   广东 
#     1      1      1      1      1      1      1      1      1      1      1 
#  广西   海南   四川   陕西   新疆   安徽   贵州   云南   甘肃   青海   宁夏 
#     1      1      1      1      1      2      2      2      2      2      2 
#  北京   天津   山西   辽宁   吉林 黑龙江   上海   西藏 
#     3      3      3      3      3      3      3      4 

　　

结果：

博文源代码和习题均来自于教材《统计建模与R软件》（ISBN：9787302143666，作者：薛毅）。