算法运行时间复杂度

算法的运行时间复杂度分析，一般是求输入规模作为自变量，运行时间作为因变量的函数。并不是求所有语句执行的真实代价，是考虑算法运行时间的增长率（增长的量级），只求出公式中的最高次项，忽略低次项和系数。

经常的情况是，输入规模相同，但某种输入会使算法的运行时间其他输入更长。所以算法的时间复杂度可能会有个定语修饰。

 最坏情况下：某种输入下，运行时间最长的情况

平均情况下：概率分布分析，算法时间复杂度的期望

最好情况下：某种输入下，运行时间最短的情况

 

时间复杂度分析用到的渐进记号

O：算法运行的渐近上界

当得到算法在最坏情况下运行时间上界为O(f(n))，可以说算法在任何情况下运行时间上界是O(f(n)). 因此特性，多数时候要求找到算法的渐近上界。

Ω：算法运行的渐近下界

当得到算法在最好情况下运行时间下界为 Ω(f(n))，可以说算法在任何情况下运行时间下界是 Ω(f(n)).

θ：算法运行的确界

算法运行时间T(n)=θ(f(n))当且仅当算法时间复杂度T(n)=O(f(n))且T(n)=Ω(f(n))   

o记号：非渐近紧确的上界

比如：T(n)=2n，有T(n)=O(n).那么n^2是T(n)的上界，但不是紧确的上界，有T(n)=o(n^2)

ω记号：非渐近紧确的下界，ω和Ω的关系如o和O的关系

 几种常见的算法运行时间渐近上界，根据函数性质可知运行时间对比（输入规模足够大）：

O(1)<O(log(2,n))<O(n)<O(nlog(2,n))<O(n^2)<O(n^3)<O(n^k)<O(2^n)<O(n!)

 

算法时间复杂度可以通过对代码迭代次数分析得到，当算法包含递归过程时，时间复杂度分析将变得稍费周折。下边对递归算法时间复杂度计算做一个学习总结。

递归算法的时间复杂度分析主要采用以下3种方法：

代入法：对复杂度做预测，将预测代入原来的递归方程，没出现矛盾则是可能的解，最后用数学归纳法证明

比如：递归式T(n)=2T(n/2)+n ，猜测T(n)=O(nlgn) 。我们需要证明存在常数c>0，T(n)<=cnlgn

假设这个上界对n/2成立，即T(n/2)=1/2cnlg(n/2)

则T(n)=2T(n/2)+n=cnlg(n/2)+n=cnlgn-n(c-1)，使得T(n)<=cnlgn，只要c>=1即可，证明完毕

 

迭代法：根据T(n)和T(n-1)的关系，逐渐递推至T(1)。采用递归树对递归过程进行分析，得出T(n)的渐近上界

 还举上边的例子，递归式T(n)=2T(n/2)+n，画出递归树分析代价：

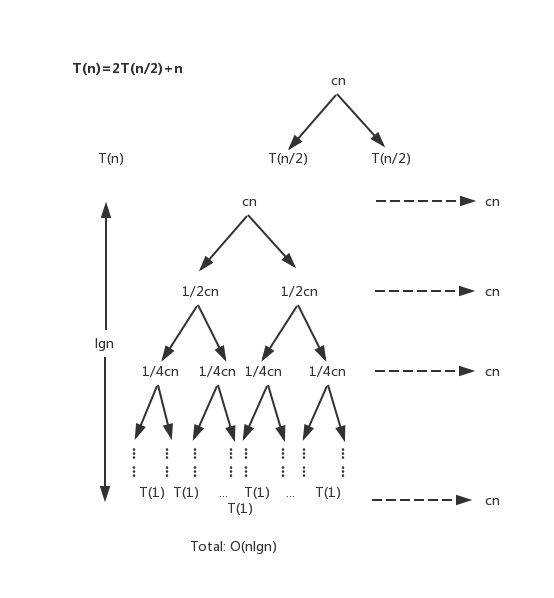
由此得出T(n)=O(nlgn)

 

公式法（主函数法）：

递归时间复杂度分析有形如T(n)=aT(n/b)+f(n);  (a>=1&&b>1且均为常数，f(n)是确定的正函数)：

可直接得出算法的时间复杂度：

T(n)=O(n^log(b,a)); //当O(n^log(b,a))>O(f(n))且是多项式的大

T(n)=O(log(2,n)*f(n));//当O(n^log(b,a))==O(f(n))

T(n)=O(f(n)); //当O(n^log(b,a))<O(f(n))且是多项式的小

多项式的大：

比如，n^2.1大于n^2, 且是多项式的大于

但n虽大于lgn，但不是多项式的大于l

由于递归多数形式是T(n)=aT(n/b)+f(n)，所以主方法非常简单好用。

 

常见递归算法复杂度

T(n)=T(n-1)+O(1);   //迭代法递归树分析，时间复杂度O(n)

T(n)=2T(n-1)+O(1);  //如果通过递归树分析，得时间复杂度 O(2^n)，但明显递归过程出现大量重叠子问题，通过动态规划或者备忘录方法，可以令时间复杂度降为O(n)

T(n)=2T(n/2)+O(n); //主方法，时间复杂度O(nlgn)

T(n)=2T(n/2)+O(n^2);  //主方法，时间复杂度O(n^2)