源码阅读(13):Java中主要的Queue、Deque结构——PriorityQueue集合(中)
(接上文《源码阅读(12):Java中主要的Queue、Deque结构——PriorityQueue集合(上)》)
3.3、PriorityQueue集合核心工作原理
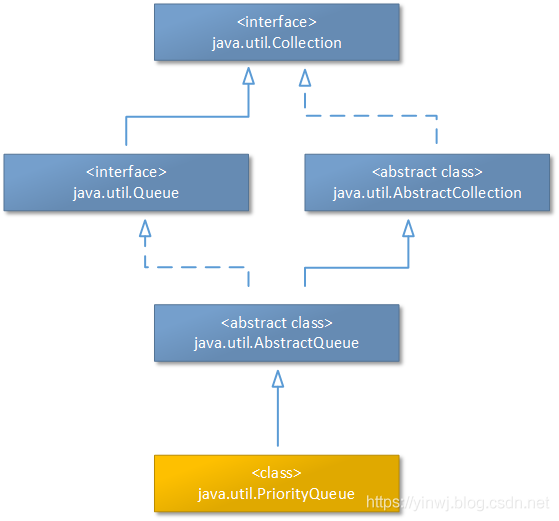
PriorityQueue集合为了保证读写性能的平衡性,所以在其中始终维护着一个堆结构(默认是小顶堆,也可能在程序员更改Comparator接口的实现逻辑后,转变成一个大顶堆结构)。这句和如何理解呢?也就是说PriorityQueue集合每进行一次写操作,都会针对集合中新的数据情况进行调整,保证集合中所有数据始终按照小顶堆/大顶堆的结构特点进行排列。
小顶堆结构是指这样的完全二叉树结构:其任意一个非叶子结点的权值,都不大于其左右儿子结点的权值。
PriorityQueue集合内部使用一个数组变量存储数据,变量名为queue——也就是实现了上文中重点描述的通过数组形式进行完全二叉树的降维表达(具体情况请参见上一篇文章)。
3.3.1、堆树的升序操作
这里提到的写操作无非就是两种情况,一种情况是向PriorityQueue集合添加新的数据;另一种情况是从PriorityQueue集合移除已有数据。由于PriorityQueue集合始终维护着一个堆结构,所以当添加新的数据时,实际上只有当前添加的数据需要重新调整存储的索引位置,以便重新将整个PriorityQueue集合的内部结构维护成小顶推。
在queue数组当前已存储数据的最后一个有效缩影 + 1的位置添加新的数据,按照完全二叉树的降维原理,这个索引位一定是当前二叉树的最后一个叶子结点。如下图所示(本文所有示例均基于小顶堆):
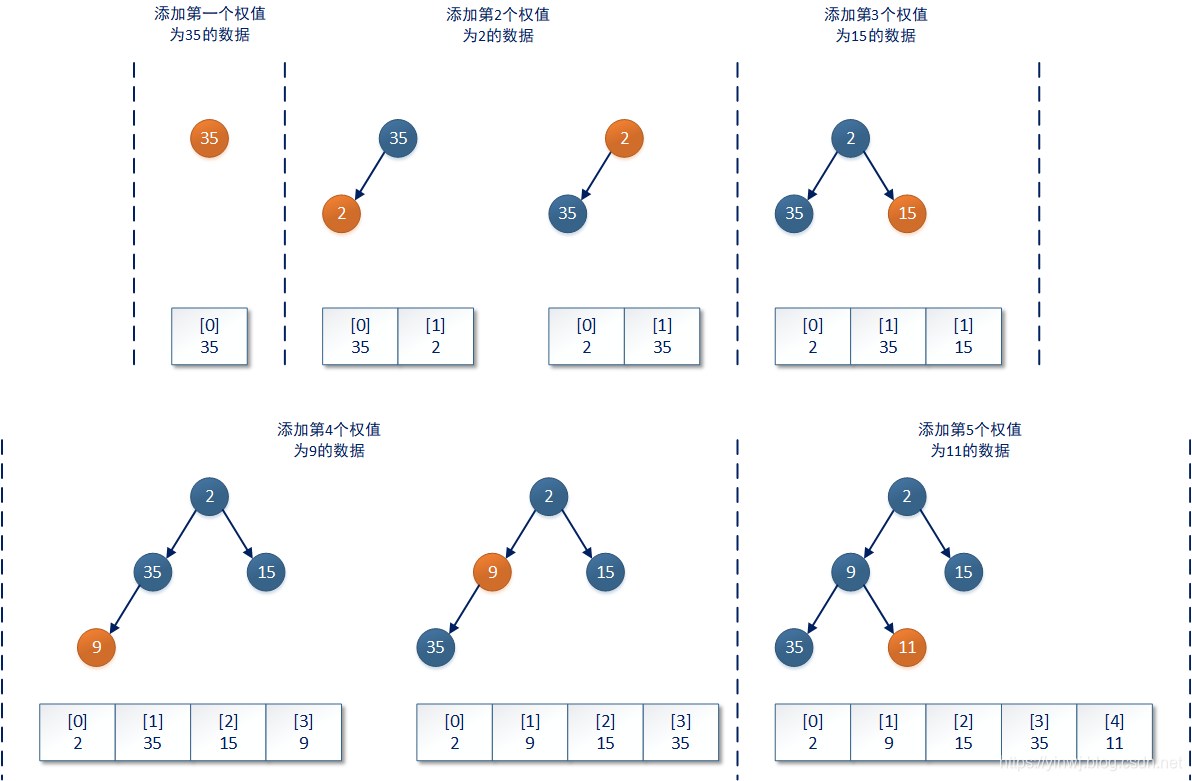
每次新添加的数据一定首先存放在完全二叉树的最后一个叶子结点上,如果按照数组进行表示,那么新添加的数据一定在数组的最后一个有效索引位上(注意,不是当前数组的最后一个位置)。接着PriorityQueue集合会验证新添加数据后整个完全二叉树是否还是一个堆树结构,如果不是则需要进行最后一个数据的升序操作。
该数据的升序操作将一直进行到它的权值不大于它的双亲结点(父结点)或者它成为整个完全二叉树的根结点为止。这样一来PriorityQueue集合又会重新满足小顶堆/大顶堆的结构。本次操作完成后,PriorityQueue集合才会进行下一个新数据的写操作。PriorityQueue集合中和该升序操作相关的代码如下所示:
// ......
// 该方法用于在完全二叉树指定的索引位置k添加新的数据x
// 并且为了保证堆结构的稳定(默认为小顶堆),将从k的位置开始,调整x数据到符合要求的索引位置(升序操作)。
private void siftUp(int k, E x) {
// 该方法根据场景的不同实际上调用了两种不同的方法
// 当PriorityQueue集合独立设定了comparator比较器对象,那么调用siftUpUsingComparator方法
// 其它情况调用siftUpComparable方法。
if (comparator != null)
siftUpUsingComparator(k, x);
else
siftUpComparable(k, x);
}
@SuppressWarnings("unchecked")
private void siftUpComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
// 如果条件成立,说明变量k表达的索引位,依然在当前queue数组的有效索引范围内
while (k > 0) {
// 通过计算得到当前索引为的父级索引位
// 如果不能理解这句话,请参见上文介绍的堆树降维后在数组上的结构表单方式。
int parent = (k - 1) >>> 1;
Object e = queue[parent];
// 如果当前要插入的数据实现的Comparable接口中的权值对比结果是:
// 当前结点的权值大于父级结点的权值,则说明当前结点不能再进行升序了
// 跳出while循环
if (key.compareTo((E) e) >= 0)
break;
// 执行到这里,说明当前结点上的数据(k代表的索引位)需要何其父结点的索引位上的数据进行交换
// 于是通过以下代码首先将e代表的父结点上的数据赋值(引用)到当前结点。
queue[k] = e;
// 将parent代表的索引位赋值给k,准备下一次循环对比。
k = parent;
}
queue[k] = key;
}
// 该方法的思路和siftUpComparable()方法中的逻辑思路一致,这里就不需要再进行赘述了
// 本方法中唯一不同点是comparator接口的实现并不是来自于将要添加的x对象。
// 而是来自于PriorityQueue集合构造函数中的设定。
@SuppressWarnings("unchecked")
private void siftUpUsingComparator(int k, E x) {
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = queue[parent];
if (comparator.compare(x, (E) e) >= 0)
break;
queue[k] = e;
k = parent;
}
queue[k] = x;
}
// ......
以上和完全二叉树升序操作相关的代码片段中,关键的知识点已经在上文中进行过介绍了。例如通过“(k - 1) >>> 1”的方式,可以找到当前索引位k的双亲结点(父结点)所在的索引位;另外,关于java.util.Comparator接口的实现和使用方式,本文会认为各位读者都已知晓,所以不在这里展开进行叙述了。
3.3.2、堆树的降序操作
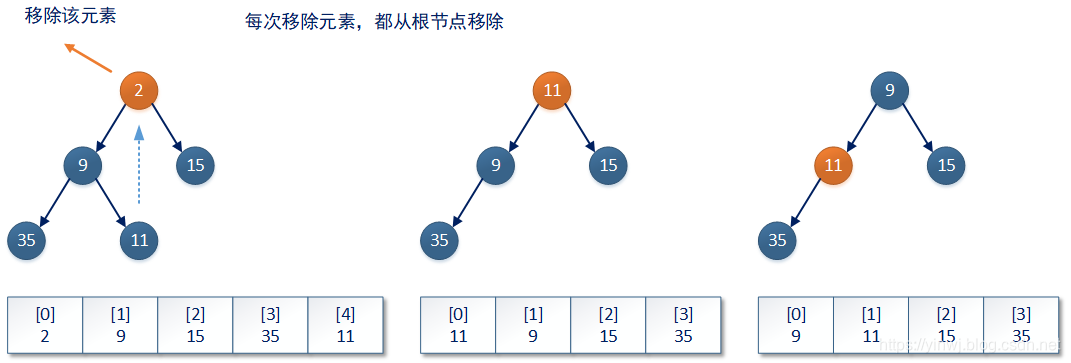
在PriorityQueue集合移除数据时,会移除根结点上的数据——也就是queue数组中第0号索引位上的数据。并且PriorityQueue集合会将当前queue数组最后一个有效索引位上的数据(也就是完全二叉树上最后一个叶子结点上的数据)替换到根结点上。
接着,PriorityQueue集合会判断当前整个完全二叉树是否还能保持堆结构状态。如果不能,则基于当前最新的完全二叉树结构,将根结点上的数据进行降序操作,直到整个完全二叉树重新恢复到小顶堆/大顶堆结构。PriorityQueue集合中和该降序操作相关的代码如下所示(以下代码只描述降序操作本身,并不包括数据的移除操作):
// 该方法用于在完全二叉树指定的索引位置k添加新的数据x
// 并且为了保证堆结构的稳定,将从k的位置开始,调整x数据到符合要求的索引位置(降序操作)。
private void siftDown(int k, E x) {
if (comparator != null)
siftDownUsingComparator(k, x);
else
siftDownComparable(k, x);
}
@SuppressWarnings("unchecked")
private void siftDownComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>)x;
// 首先要说明的是,判定一个结点是否需要进行降序,那么肯定是在非叶子结点判定的
// 因为叶子结点是无法降序的,所以通过以下代码,可以获得当前完全二叉树上
// 最后一个(索引位最大的一个)非叶子结点的索引位。
int half = size >>> 1; // loop while a non-leaf
// 如果条件成立,说明还有可能继续进行降序判定
while (k < half) {
// 通过当前语句,取得当前结点的左儿子结点的索引位置
// 注意,作为一个完全二叉树的数组结构表达,一个非叶子结点一定存在左儿子结点
int child = (k << 1) + 1; // assume left child is least
Object c = queue[child];
// 取得的左儿子索引位置+1,就是当前结点K的右儿子索引位置的值
// 但不同的是,当前非叶子结点不一定有右儿子。
int right = child + 1;
// 如果条件成立,说明当前结点存在右儿子结点,且右儿子结点上的数据权值小于左儿子上的数据权值
// 那么这时,就将使用当前结点右儿子结点的数据权值在下一步和当前结点的权值进行比较
if (right < size && ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
c = queue[child = right];
// 如果条件成立,就说明当前结点的数据权值小于等于其权值较小的儿子结点。
// 那么当前结点的数据就不必再进行降序了,跳出while循环
if (key.compareTo((E) c) <= 0)
break;
// 如果程序运行到这里,就说明当前结点的数据需要和其权值较小的数据结点进行交换
queue[k] = c;
// 设置较小数据权值的儿子结点的索引位为k,为下一循环的对比操作做好准备
k = child;
}
// 以上循环比较降序操作结束后,当前k指向的索引位就是新插入的数据最终存放的索引位。
queue[k] = key;
}
// 该方法的思路和siftDownComparable()方法中的逻辑思路一致,这里也就不需要再进行赘述了
// 本方法中唯一不同点也是comparator接口的实现并不是来自于将要添加的x对象。
// 而是来自于PriorityQueue集合构造函数中的设定。
@SuppressWarnings("unchecked")
private void siftDownUsingComparator(int k, E x) {
int half = size >>> 1;
while (k < half) {
int child = (k << 1) + 1;
Object c = queue[child];
int right = child + 1;
if (right < size &&
comparator.compare((E) c, (E) queue[right]) > 0)
c = queue[child = right];
if (comparator.compare(x, (E) c) <= 0)
break;
queue[k] = c;
k = child;
}
queue[k] = x;
}
3.3.3、完全二叉树的修复性排序(基于小顶堆)
在某些情况下PriorityQueue集合中的小顶堆结构需要进行修复性排序,这是由于在某些操作后PriorityQueue集合中的数据不再保证是一个小顶堆结构。典型的操作是某个PriorityQueue实例基于一个指定的集合进行初始化时,代码片段如下所示:
// ......
private void initElementsFromCollection(Collection<? extends E> c) {
Object[] a = c.toArray();
// If c.toArray incorrectly doesn't return Object[], copy it.
if (a.getClass() != Object[].class)
a = Arrays.copyOf(a, a.length, Object[].class);
int len = a.length;
if (len == 1 || this.comparator != null)
for (int i = 0; i < len; i++)
if (a[i] == null)
throw new NullPointerException();
this.queue = a;
this.size = a.length;
}
/**
* Initializes queue array with elements from the given Collection.
* @param c the collection
*/
private void initFromCollection(Collection<? extends E> c) {
initElementsFromCollection(c);
heapify();
}
// ......
根据以上代码我们能够知道,PriorityQueue集合在参照其它集合完成对象实例化过程时,其它参照集合中的所有数据将被依次复制(引用)到PriorityQueue集合的queue数组中,由于参照集合中的数据不一定保证是按照小顶堆结构存储的——实际上大多数情况都是这样,所以在完成复制(引用)操作后queue数组中的一个或者多个数据也不一定是按照小顶堆结构存储的。这时PriorityQueue集合就会使用一个名叫heapify()的方法,对PriorityQueue集合中的数据进行小顶堆排序,代码片段如下所示:
/**
* 无论PriorityQueue集合的queue数组中以前存储的数据顺序如何,
* 通过该方法都可以重建小顶堆结构
* Establishes the heap invariant (described above) in the entire tree,
* assuming nothing about the order of the elements prior to the call.
*/
@SuppressWarnings("unchecked")
private void heapify() {
for (int i = (size >>> 1) - 1; i >= 0; i--)
siftDown(i, (E) queue[i]);
}
堆排序的过程实际上是对queue数组中所有“非叶子”结点的数据按照权值进行降序操作。基于小顶堆的降序排序方法,比上文中介绍的比较传统的堆排序算法性能更好、空间复杂度更低。以上代码的排序过程可以用下图进行表达:
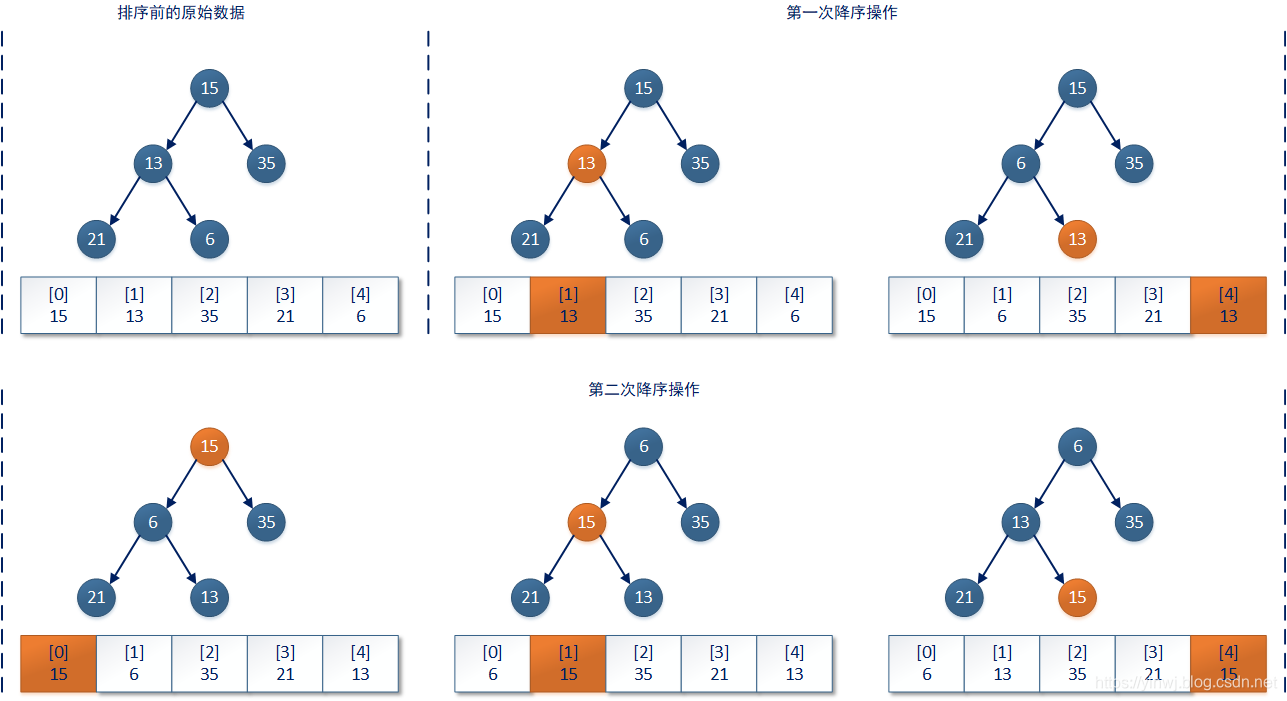
在PriorityQueue集合中有两处调用了heapify()方法,分别是上文已经提到的涉及实例初始化过程的initFromCollection()方法中,原因就是通过复制(引用)得到的新的queue数组不一定是小顶堆结构;另一处是PriorityQueue集合中和序列化操作有关的readObject()方法,Java官方的解释是:
Elements are guaranteed to be in “proper order”, but the spec has never explained what that might be.
========================
(接下文《源码阅读(14):Java中主要的Queue、Deque结构——PriorityQueue集合(下)》)


