图论总结 for noip
图论 |
很重要的数据结构，noip考试的热点，灵活多变，富有挑战性。
图的存储
邻接矩阵：n2，对稠密图较好，floyd算法的基础，但是在运用时总是需要o(n)的查找，故效率较低，运用的不多仅限数据范围很小时。而且无法处理两点之间多条边的情况（除了最……路）。
前向星：类似邻接表，利用排序将一个点的邻接节点放在一起，再通过first数组实现邻接表的功能，有些情况下要比邻接表的效率高。代码如下：
for i:=1 to m do
readln(x[i],y[i],len[i]);
sort(1,m);
for i:=1 to m do
if first[x[i]]=0 then
first[x[i]]:=i;
first[n+1]:=m+1;
for i:=n downto 1 do
if first[i]=0 then
first[i]:=first[i+1];
邻接表：只与边数有关，适用于n很大的稀疏图，也适用于两点之间多条边的情况。效率高，用链表实现，是很优秀的结构。
边表：用静态的数组a[0..maxn,0..maxn] of record模仿链表，少了next，对内存要求高，只适用于n较小的情况。
遍历
就是从某点出发，以深度优先或广度优先的顺序遍历整个图，每个顶点被访问一次。看上去很简单，但这是以后许多重要算法的基础。
也有直接考察遍历的题：
公司控制
问题
有些公司是其他公司的部分拥有者，因为他们获得了其他公司发行的股票的一部分。例如，福特公司拥有马自达公司12%的股票。据说，如果至少满足了以下三个条件之一，公司A就可以控制公司B了：
公司A = 公司B。
公司A拥有大于50%的公司B的股票。
公司A控制K(K >= 1)个公司，记为C1, ..., CK，每个公司Ci拥有xi%的公司B的股票，并且x1+ .... + xK > 50%。
给你一个表，每行包括三个数(i,j,p)；表明公司i享有公司j的p%的股票。计算所有的数对(h,s)，表明公司h控制公司s。至多有100个公司。
写一个程序读入N组数(i,j,p)，i,j和p是都在范围(1..100)的正整数，并且找出所有的数对(h,s)，使得公司h控制公司s。
INPUT FORMAT
第一行： N，表明接下来三对数的数量。{即(i,j,p)的数量}
第二行到第N+1行： 每行三个整数作为一个三对数(i,j,p)，如上文所述。{表示i公司拥有j公司 p%的股份}
SAMPLE INPUT (file concom.in)
3
1 2 80
2 3 80
3 1 20
OUTPUT FORMAT
输出零个或更多个的控制其他公司的公司。每行包括两个整数A、B,表示A公司控制了B公司。将输出的数对以升序排列。
请不要输出控制自己的公司。
[编辑]SAMPLE OUTPUT (file concom.out)
1 2
1 3
2 3
分析:
一个公司a想控制另一个公司b，那么或者直接控制，或者间接控制。直接控制不用说，如果间接控制，那么a一定是通过在拓扑序列中离自己较近的，进而控制在拓扑序列中离自己较远的。那么这就符合了有向图遍历的先后顺序。如果一个点能控制离他较近的点，那么他才能去通过改点去控制其他点。
遍历的起点不同，结果便不同。我们便可以通过枚举起点，和深度优先搜索，找到该起点对其他点的控制程度d[i]，最后输出即可。
能用遍历解决的问题，一定存在某种递归定义，或者先后顺序。只有这样，才能保证正确性。
Code
program liukeke;
var
d:array[0..101] of longint;
a:array[0..101,0..101] of longint;
v:array[0..101] of boolean;
map:array[0..101,0..101] of longint;
i,j,n,m:longint;
procedure init;
var
i,x,y,z:longint;
begin
readln(m);
for i:=1 to m do
begin
readln(x,y,z);
if x>n then n:=x;
if y>n then n:=y;
inc(a[x,0]);
a[x,a[x,0]]:=y;
map[x,y]:=z;
end;
end;
procedure dfs(x:longint);
var
i:longint;
begin
if v[x] then exit;
v[x]:=true;
for i:=1 to a[x,0] do
begin
inc(d[a[x,i]],map[x,a[x,i]]);
if d[a[x,i]]>=50 then dfs(a[x,i]);
end;
end;
begin
assign(input,'concom.in');reset(input);
assign(output,'concom.out');rewrite(output);
init;
for i:=1 to n do
begin
fillchar(d,sizeof(d),0);
fillchar(v,sizeof(v),0);
dfs(i);
for j:=1 to n do
if j<>i then
if d[j]>=50 then
writeln(i,' ',j);
end;
close(input);close(output);
end.
好多有关连通性的题目都与遍历相关，下面会介绍到。
图的连通性问题
强连通分量
在某图的子图中，任意两点都能相互到达，那么该子图就是一个强连通分量。一般情况下找的是极大强连通分量。强连通分量是有向图的特性。
有两种算法，下面给出比较直观的Kosaraju算法：
A正向邻接表 a1反向邻接表:
procedure dfs1(s:longint);
var
i:longint;
begin
if v[s] then exit;
v[s]:=true;
for i:=1 to a[s,0] do
dfs1(a[s,i]);
inc(p);
b[p]:=s;
end;
procedure dfs2(s:longint);
var
i:longint;
begin
if v[s] then exit;
v[s]:=true;
c[s]:=color;
for i:=1 to a1[s,0] do
dfs2(a1[s,i]);
end;
//main
for i:=1 to n do
if not v[i] then
dfs1(i);
fillchar(v,sizeof(v),0);
for i:=p downto 1 do
if not v[b[i]] then
begin
inc(color);
dfs2(b[i]);
end;
强连通分量常用来缩点，也就是到达任意一个点即可。
看两道例题:
例一：schlnet
问题：
一些学校连入一个电脑网络。那些学校已订立了协议：每个学校都会给其它的一些学校分发软件（称作“接受学校”）。注意即使 B 在 A 学校的分发列表中， A 也不一定在 B 学校的列表中。
你要写一个程序计算，根据协议，为了让网络中所有的学校都用上新软件，必须接受新软件副本的最少学校数目（子任务 A）。更进一步，我们想要确定通过给任意一个学校发送新软件，这个软件就会分发到网络中的所有学校。为了完成这个任务，我们可能必须扩展接收学校列表，使其加入新成员。计算最少需要增加几个扩展，使得不论我们给哪个学校发送新软件，它都会到达其余所有的学校（子任务 B）。一个扩展就是在一个学校的接收学校列表中引入一个新成员。
[编辑]格式
PROGRAM NAME: schlnet
INPUT FORMAT 输入文件的第一行包括一个整数 N：网络中的学校数目（2 <= N <= 100）。学校用前 N 个正整数标识。接下来 N 行中每行都表示一个接收学校列表（分发列表）。第 i+1 行包括学校 i 的接收学校的标识符。每个列表用 0 结束。空列表只用一个 0 表示。
OUTPUT FORMAT
你的程序应该在输出文件中输出两行。第一行应该包括一个正整数：子任务 A 的解。第二行应该包括子任务 B 的解。
[编辑]SAMPLE INPUT (file schlnet.in)
5
2 4 3 0
4 5 0
0
0
1 0
[编辑]SAMPLE OUTPUT (file schlnet.out)
1
2
分析：
为什么可以缩点呢，显然如果存在强连通分量，那么只要到达任意一个节点，即可到达该强连通分量中的所有点。那么强连通分量完全能看成一个点。
我们称入度为0的强连通分量为最高强连通分量。显然，每个最高强连通分量都必须单独发送一次软件，而其他强连通分量都可以通过最高强连通分量到达。所以，最高强连通分量的个数也就是问题A的解。
第二问就是，问至少添加多少条边，才能使原图强连通。也就问在收缩后的图至少添加多少条边，才能使之强连通。
可以知道，"存在一个顶点入度为0或者出度为0"与"该图一定不是强连通的"是等价的命题。为了使添加的边最少，则应该把入度为0顶点和出度为0的顶点每个顶点添加1条边，使图中不存在入度为0顶点和出度为0的顶点。
当入度为0的顶点多于出度为0的顶点，则应添加的边数应为入度为0的顶点的个数。当出度为0的顶点多于出入度为0的顶点，则应添加的边数应为出度为0的顶点的个数。
这样就可以解决问题了。但是不要忘了还有特殊的情况，当原图本身就是强连通分量时，收缩成一个顶点，该顶点入度和出度都为0，但第一问应为1，第二问应为0。
Code:
{
ID: liukeke
PROG: schlnet
LANG: PASCAL
}
program liukeke;
var
map:array[0..101,0..101] of boolean;
a,a1:array[0..101,0..101] of longint;
into,outto,b,c:array[0..101] of longint;
v:array[0..101] of boolean;
i,j,ans1,ans2,p,color,n:longint;
procedure init;
var
i,x,y:longint;
begin
readln(n);
for i:=1 to n do
begin
x:=i;
read(y);
while y<>0 do
begin
inc(a[x,0]);
a[x,a[x,0]]:=y;
map[x,y]:=true;
inc(a1[y,0]);
a1[y,a1[y,0]]:=x;
read(y);
end;
end;
end;
procedure dfs1(s:longint);
var
i:longint;
begin
if v[s] then exit;
v[s]:=true;
for i:=1 to a[s,0] do
dfs1(a[s,i]);
inc(p);
b[p]:=s;
end;
procedure dfs2(s:longint);
var
i:longint;
begin
if v[s] then exit;
v[s]:=true;
c[s]:=color;
for i:=1 to a1[s,0] do
dfs2(a1[s,i]);
end;
begin
assign(input,'schlnet.in');reset(input);
assign(output,'schlnet.out');rewrite(output);
init;
for i:=1 to n do
if not v[i] then
dfs1(i);
fillchar(v,sizeof(v),0);
for i:=p downto 1 do
if not v[b[i]] then
begin
inc(color);
dfs2(b[i]);
end;
if color=1 then
begin
writeln(1);
writeln(0);
close(input);
close(output);
halt;
end;
for i:=1 to n do
for j:=1 to n do
if i<>j then
if (c[i]<>c[j])and(map[i,j]) then
begin
inc(into[c[j]]);
inc(outto[c[i]]);
end;
ans1:=0;
ans2:=0;
for i:=1 to color do
begin
if into[i]=0 then inc(ans1);
if outto[i]=0 then inc(ans2);
end;
writeln(ans1);
if ans1>ans2 then writeln(ans1)
else writeln(ans2);
close(input);
close(output);
end.
例题2 间谍网络
问题
给定一个有向图，图中某些节点能用一定的价值通知到，而其他节点只能用与之相连的节点通知到。问你将图中所有节点通知到的最小代价。(n<=3000)
分析
有了上面一题的基础，就很容易看出此题要用强连通分量缩点。这类”到达“问题通常要用强连通分量缩点。这里的缩点，其实是利用c数组的值，重新构图。
之后，我们能得到三个显然的性质：
1、 如果n个点在一个强连通分量中，一定优先通知最小的。
2、 如果一个强连通分量无入度，那么它一定需要通知。
3、 如果一个强连通分量有入度，那么它一定无需通知。
仔细分析后，发现这不就是上一题的第一问吗，不过多了一个价值的限制
由此，我们能归纳出强连通分量解决“到达问题“的思路。利用强连通分量重新构图，之后将问题转化为与新节点的度相关的问题。再具体问题具体分析即可。
当然强联同分量的应用是很广泛的，这里只是一方面。也是最常考察的方面。
Code（略）
除了强连通分量之外还有与图的联通性直接关联的问题，这类问题往往用到删点的思想，结合dfs遍历：
例题：race
问题
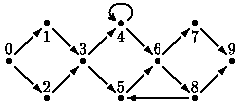图一表示一次街道赛跑的跑道。可以看出有一些路口（用 0 到 N 的整数标号），和连接这些路口的箭头。路口 0 是跑道的起点，路口 N 是跑道的终点。箭头表示单行道。运动员们可以顺着街道从一个路口移动到另一个路口（只能按照箭头所指的方向）。当运动员处于路口位置时，他可以选择任意一条由这个路口引出的街道。
图一：有 10 个路口的街道 一个良好的跑道具有如下几个特点：
每一个路口都可以由起点到达。
从任意一个路口都可以到达终点。
终点不通往任何路口。
运动员不必经过所有的路口来完成比赛。有些路口却是选择任意一条路线都必须到达的（称为“不可避免”的）。在上面的例子中，这些路口是 0，3，6，9。对于给出的良好的跑道，你的程序要确定“不可避免”的路口的集合，不包括起点和终点。
假设比赛要分两天进行。为了达到这个目的，原来的跑道必须分为两个跑道，每天使用一个跑道。第一天，起点为路口 0，终点为一个“中间路口”；第二天，起点是那个中间路口，而终点为路口 N。对于给出的良好的跑道，你的程序要确定“中间路口”的集合。如果良好的跑道 C 可以被路口 S 分成两部分，这两部分都是良好的，并且 S 不同于起点也不同于终点，同时被分割的两个部分满足下列条件：（1）它们之间没有共同的街道（2）S 为它们唯一的公共点，并且 S 作为其中一个的终点和另外一个的起点。那么我们称 S 为“中间路口 ”。在例子中只有路口 3 是中间路口。（注： 其实简而言之就是说第二天除了中间路口无论怎么跑也跑不到第一天的路口上）
[编辑]格式
PROGRAM NAME: race3
INPUT FORMAT:
(file race3.in)
输入文件包括一个良好的跑道，最多有 50 个路口，100 条单行道。
一共有 N+2 行，前面 N+1 行中第 i 行表示以编号为(i-1)的路口作为起点的街道，每个数字表示一个终点。行末用 -2 作为结束。最后一行只有一个数字 -1。
OUTPUT FORMAT:
(file race3.out)
你的程序要有两行输出：
第一行包括：跑道中“不可避免的”路口的数量，接着是这些路口的序号，序号按照升序排列。
第二行包括：跑道中“中间路口”的数量，接着是这些路口的序号，序号按照升序排列。
[编辑] SAMPLE INPUT
1 2 -2
3 -2
3 -2
5 4 -2
6 4 -2
6 -2
7 8 -2
9 -2
5 9 -2
-2
-1
[编辑] SAMPLE OUTPUT
2 3 6
1 3
分析
从题目描述就能看出，是与图的连通性紧密相关。Dfs必不可少，关键是如何运用。往往都是，攻克了这里，题目也就解决了
第一问，求有向图的必经节点，这个问题很具有普遍性。枚举节点，删去该节点，之后从1点开始遍历，如果无论如何都无法到达n，改点就是必经节点。这是从反面入手对问题的解决。
第二问，有向图的割点。首先，它一定是必经节点。
枚举割点，从割点开始dfs，与删去该割点从0dfs相比，如果不存在两次dfs都能到达的节点，证明改点是割点。
Dfs只能说是工具，这道题的关键是枚举和交集的思想。那么其它题就可能涉及其它算法与dfs的结合了。
Code
{
ID: liukeke
PROG: race3
LANG: PASCAL
}
program liukeke;
var
a:array[0..60,0..60] of longint;
v1:array[0..60,0..60] of boolean;
v2:array[0..60] of boolean;
can:array[0..60] of boolean;
ans1,ans2:array[0..60] of longint;
tot,tot2,n:longint;
procedure init;
var
i,x:longint;
begin
n:=-1;
while true do
begin
read(x);
if x=-1 then break;
inc(n);
while x<>-2 do
begin
inc(a[n,0]);
a[n,a[n,0]]:=x;
read(x);
end;
if x=-2 then readln;
end;
end;
procedure dfs1(x:longint);
var
i:longint;
begin
if v1[tot,x] then exit;
if can[x] then exit;
v1[tot,x]:=true;
for i:=1 to a[x,0] do
dfs1(a[x,i]);
end;
procedure dfs2(x:longint);
var
i:longint;
begin
if v2[x] then exit;
v2[x]:=true;
for i:=1 to a[x,0] do
dfs2(a[x,i]);
end;
procedure main1;
var
i,j:longint;
begin
tot:=1;
for i:=1 to n-1 do
begin
can[i]:=true;
for j:=0 to n do
v1[tot,j]:=false;
dfs1(0);
if not v1[tot,n] then
begin
ans1[tot]:=i;
inc(tot);
end;
can[i]:=false;
end;
dec(tot);
write(tot);
for i:=1 to tot do
write(' ',ans1[i]);
writeln;
end;
procedure main2;
var
i,j:longint;
flag:boolean;
begin
for i:=1 to tot do
begin
fillchar(v2,sizeof(v2),0);
dfs2(ans1[i]);
flag:=false;
for j:=0 to n do
if (v2[j]) and (v1[i,j]) then
begin
flag:=true;
break;
end;
if not flag then
begin
inc(tot2);
ans2[tot2]:=ans1[i];
end;
end;
write(tot2);
for i:=1 to tot2 do
write(' ',ans2[i]);
writeln;
end;
begin
assign(input,'race3.in');reset(input);
assign(output,'race3.out');rewrite(output);
init;
main1;
main2;
close(input);
close(output);
end.
无向图最小生成树。
先注意，是无向图最小生成树。
1、 先要介绍两个基本的算法，这不是多此一举，正确的应用往往是建立在深刻理解之上的。
(1) Prim
将整个图分成两个集合，一个集合中的点已在最小生成树中，另一个集合中的点不在最小生成树中，每次将两集合的交叉边中最小的一条相连的不在生成树集合的点加入生成树集合中，直到加入了n-1条边为止。
显然复杂度与点的个数有关，为o(n2),必要时用堆优化。适用于点数较少的稠密图。代码略。
(2) Kruscal
将边排序，每次将最小的边的两端加入生成树集合，直到所有节点都在一个集合为止。
算法要点：Kruskal算法的最难点在于怎样判断加入边(x,y)后是否形成了环（生成树要保证无环）。
问题可化为： 判断边(x,y)的两个顶点x,y在图（实际是森林）mst中是否已经连通。如果已经连通，加入边将形成环；否则，不形成环。
并查集：连通点集之类问题，有高效算法---并查集
代码略
下面是最小生成树的例题了：（这里裸的最小生成树就没有必要说了）
例1 brog maze
问题
给出一个n*m（<=50）的迷宫。里面有s和a，二者都可以移动。开始时只有s会移动（特别注意s可以分开，a也可以分开，就是同时多向行动），它的目标就是找a，当他找到a后，找到的a也会帮他去找a，可以说，只要找到a，a就被同化了，问最少的总步数（a和s）使得所有a都被同化。
分析
一看就会想到搜索，但是搜索的状态数太多，很难做。再仔细分析，找到a就被同化。我们可以先将a和s看成一样的节点。能用宽搜处理出任意两个字母之间的距离。这样把每个字母看成节点，就能构出一个无向图。那要找的是什么?
根据题意的“分离”规则，重复走过的路不再计算（这是关键），如果不能分离，就只好用搜索做。
因此当使用prim算法求L的长度时，根据算法的特征恰好不用考虑这个问题（源点合并很好地解决了这个问题），L就是最少生成树的总权值W
遍历每个节点，而且总步数最少——最小生成树！
为了方便查找，开一个which数组。点的坐标做下标，对应第几个点是数组中的值。
要敢于大胆猜想。破除惯性思维，找到题目的特点，发掘图论模型。
Code
program liukee;
type xz=record
x:longint;
y:longint;
z:longint;
end;
var
d:array[1..4,1..2] of integer=((1,0),(-1,0),(0,1),(0,-1));
x1,y1:array[1..101] of longint;
map:array[0..51,0..51] of char;
which:array[0..51,0..51] of longint;
a:array[1..101,1..101] of longint;
mincost:array[1..101] of longint;
zu,n,m,ans,tt,i:longint;
procedure init;
var
i,j:longint;
xxx:char;
s:string;
begin
tt:=0;
readln(m,n);
readln(s);
for i:=2 to n do
begin
for j:=1 to m do
begin
read(map[i,j]);
xxx:=map[i,j];
if (map[i,j]='A') or (map[i,j]='S') then
begin
inc(tt);
which[i,j]:=tt;
x1[tt]:=i;
y1[tt]:=j;
end;
end;
readln;
end;
for i:=1 to m do
begin
map[1,i]:=s[i];
if (map[1,i]='A') or (map[1,i]='S') then
begin
inc(tt);
which[i,j]:=tt;
x1[tt]:=i;
y1[tt]:=j;
end;
end;
for i:=length(s) to m do
map[1,i]:=' ';
end;
procedure doit;
var
q:array[1..100000] of xz;
v:array[1..50,1..50] of boolean;
i,l,r,xx,yy,j:longint;
begin
for i:=1 to tt do
begin
fillchar(q,sizeof(q),0);
fillchar(v,sizeof(v),0);
l:=0;
r:=1;
q[1].x:=x1[i];
q[1].y:=y1[i];
q[1].z:=0;
v[x1[i],y1[i]]:=true;
while l<r do
begin
inc(l);
for j:=1 to 4 do
begin
xx:=q[l].x+d[j,1];
yy:=q[l].y+d[j,2];
if(xx>0)and(yy>0)and(xx<=n)and(yy<=m)and(map[xx,yy]<>'#')and(not v[xx,yy])then
begin
if which[xx,yy]<>0 then
begin
a[i,which[xx,yy]]:=q[l].z+1;
// a[which[xx,yy],i]:=q[l].z+1;
end;
inc(r);
q[r].x:=xx;
q[r].y:=yy;
q[r].z:=q[l].z+1;
v[xx,yy]:=true;
end;
end;
end;
end;
end;
procedure prim;
var
i,j,k,min:longint;
begin
for i:=1 to tt do
for j:=1 to tt do
if a[i,j]=0 then a[i,j]:=maxlongint;
mincost[1]:=0;
for i:=2 to tt do
mincost[i]:=a[1,i];
for i:=1 to tt-1 do
begin
min:=maxlongint;
for j:=1 to tt do
if (mincost[j]<min)and(mincost[j]<>0)then
begin
min:=mincost[j];
k:=j;
end;
inc(ans,min);
mincost[k]:=0;
for j:=1 to tt do
if mincost[j]>a[k,j] then mincost[j]:=a[k,j];
end;
end;
begin
readln(zu);
for i:=1 to zu do
begin
ans:=0;
fillchar(a,sizeof(a),0);
fillchar(which,sizeof(which),0);
fillchar(mincost,sizeof(mincost),0);
init;
doit;
prim;
writeln(ans);
end;
end.
例2：new start
问题
【题目描述】
发展采矿业当然首先得有矿井，小FF花了上次探险获得的千分之一的财富请人在岛上挖了n口矿井，但他似乎忘记考虑的矿井供电问题……
为了保证电力的供应， 小FF想到了两种办法：
1、 在这一口矿井上建立一个发电站， 费用为v（发电站的输出功率可以供给任意多个矿井）。
2、 将这口矿井不另外的已经有电力供应的矿井之间建立电网， 费用为p。
小FF希望身为”NewBe_One" 计划首席工程师的你帮他想出一个保证所有矿井电力供应的最小花费。
【输入格式】
第一行一个整数n， 表示矿井总数。
第2～n+1行，每行一个整数， 第i个数v[i]表示在第i口矿井上建立发电站的费用。
接下来为一个n*n的矩阵P， 其中p[ i , j ]表示在第i口矿井和第j口矿井之间建立电网的费用（数据保证有p[ i, j ] = p[ j, i ], 且 p[ i, i ]=0）。
【输出格式】
仅一个整数， 表示让所有矿井获得充足电能的最小花费。
【输入样例】
4 5 4
4
3
0 2 2 2
2 0 3 3
2 3 0 4
2 3 4 0
【输出样例】
9
输出样例说明：
小FF可以选择在4号矿井建立发电站然后把所有矿井都不其建立电网，总花费是 3+2+2+2 = 9。
【数据范围】
对于30%的数据： 1<=n<=50;
对于100%的数据： 1<=n<=300; 0<=v[i], p[i,j] <=10^5.
分析
如果单纯建造电网的话，就是最简单的最小生成树了。但是，本题的难点就在于可以在任意一点新建发电站。
进一步分析，至少要有一个地点新建发电站，那么对每个点只有建发电站或是由别人供电。考虑虚拟一个0节点，该节点到其他节点的权值为在该点新建发电站的花费。之后对改图求一遍最小生成树即可。
看到电网，局域网等问题，会想到最小生成树问题。关键是解决问题的特性。虚拟节点是经常用到的好方法。
Code(略)
例3：公路建设
问题
【问题描述】
A国是一个新兴的国家，有N个城市，分别编号为1,2.3…N。
政府想大搞公路建设，提供了优惠政策：对于每一个投资方案的预计总费用，政府负担50%，并且允许投资的公司对过往的汽车收取连续5年的养路费。世界各地的大公司纷纷投资，并提出了自己的建设方案，他们的投资方案包括这些内容：公路连接的两座城市的编号，预计的总费用（假设他们的预计总师准确的）。
你作为A国公路规划局的总工程师，有权利决定每一个方案是否接受。但是政府给你的要求是：
要保证各个城市之间都有公路直接或间接相连。
因为是新兴国家，政府的经济实力还不强。政府希望负担最少的费用。
因为大公司并不是同时提出方案，政府希望每接到一个方案，就可以知道当前需要负担的最小费用和接受的投资方案，以便随时开工。关于你给投资公司的回复可以等到开工以后再给。
注意：A国一开始是没有公路的。
【数据说明】
A国的城市数目N<=500，投资的方案总数M<=2000。
【输入】
输入文件名：Road.in
第1行有两个数字：N、M
第2行到第M+1行给出了各个投资方案，第i行的方案编号为i-1
编号小的方案先接到，
一个方案占一行，每行有3个数字，分别是连接的两个城市编号a、b，和投资的预计总费用cost。
【输出】
输出文件名：Road.out
输出文件共有M行。
每一行的第一个数字是当前政府需要负担的最少费用（保留1位小数），后面是X个数字，表示当前政府接受的方案的编号，不．要求从小到大排列。但如果此时接受的所有投资方案不能保证政府的第一条要求，那么这一行只有一个数字0
【样例】
Road.in
3 5
1 2 4
1 3 4
2 3 4
1 3 2
1 2 2
Road.out
0
4.00 1 2
4.00 1 2
3.00 1 4
2.00 4 5
分析
看起来很复杂，其实就是对最小生成树进行动态维护。由kruscal算法的原理，我们知道，新加入边的两端节点只有可能有两种情况
1． 两点已经连通
2． 两点未连通
如果两点未连通，那么当前边一定加入生成树中。
如果两点已连通，则从一点开始dfs（由于是生成树，所以任意两点间路径唯一）。找到两点间路径上权值最大的边，删去该边，并将当前边加入生成树集合即可。
这样，每次读入一条边后，仍能使图保持为最小树形图。
这个算法的时空复杂度是多少呢？
>时间复杂度
每次读入一条边e(a,b)，要检查a, b之间是否有路径相连，我们需要一个深搜的过程
>如果我们用链表的话，深搜的时间复杂为O(e)，而最小树形图中最多只有n-1条边，所以这个过程为O(n)级的
然后我们要去边与加边，这都是小于O(n)级的，
所以维护的时间复杂的是O(n)级的。
因为有m要增加，我们总共要维护m次，
所以总的时间复杂度为O(n*m)级的，这是可以承受的。
从这道题，我们应该更加深刻的审视生成树的属性：
|v|-1条边、连通、无环
Code（略）
2、 无向图生成树的个数
这个东西其实属于超纲内容，不再展开讲解了。思想就是行列式求值：
http://www.cnblogs.com/saltless/archive/2010/11/06/1870778.html
code
procedure init;
var
i,j,x:longint;
begin
fillchar(a,sizeof(a),0);
readln(n,m);
inc(n);
for i:=1 to n do
begin
for j:=1 to n do
begin
read(x);
if x=1 then
begin
a[i,i]:=a[i,i]+1;
a[i,j]:=-1;
end;
end;
readln;
end;
g:=a;
end;
procedure main;
var
i,j,k:longint;
m,ans:extended;
begin
ans:=1;
for i:=1 to n-1 do
begin
ans:=ans*a[i,i];
for j:=i+1 to n-1 do
if a[j,i]<>0 then
begin
m:=-a[i,i]/a[j,i];
ans:=ans/m;
for k:=i to n-1 do
a[j,k]:=a[j,k]*m+a[i,k];
end;
end;
writeln(round(ans));
end;
3、 次小生成树问题
基于kruscal的算法：
在做最小生成树时，记录下用到过的边。之后枚举删边，再作生成树。得到的最小的就是原图的最小生成树
Code
program liukee;
var
x,y,len:array[1..1000000] of longint;
f:array[1..1000] of longint;
can:array[1..1000] of boolean;
pass:array[1..1000] of longint;
ans,n,m,i,j,min,tt,k,min1:longint;
procedure sort(l,r:longint);
var
i,j,mid,temp:longint;
begin
i:=l;j:=r;
mid:=len[(i+r) div 2];
repeat
while len[i]<mid do inc(i);
while len[j]>mid do dec(j);
if i<=j then
begin
temp:=x[i]; x[i]:=x[j]; x[j]:=temp;
temp:=y[i]; y[i]:=y[j]; y[j]:=temp;
temp:=len[i]; len[i]:=len[j]; len[j]:=temp;
inc(i);
dec(j);
end;
until i>j;
if i<r then sort(i,r);
if l<j then sort(l,j);
end;
function find(x:longint):longint;
begin
if f[x]=x then exit(x);
f[x]:=find(f[x]);
exit(f[x]);
end;
procedure union1(x,y,len:longint);
var tt1,tt2:longint;
begin
tt1:=find(x);
tt2:=find(y);
if tt1<>tt2 then
begin
inc(ans,len);
f[tt1]:=tt2;
inc(tt);
pass[tt]:=i;
end;
end;
procedure union2(x,y,len:longint);
var tt1,tt2:longint;
begin
tt1:=find(x);
tt2:=find(y);
if (tt1<>tt2)and(not can[j]) then
begin
inc(ans,len);
f[tt1]:=tt2;
end;
end;
begin
assign(input,'1.in');reset(input);
tt:=0;min:=maxlongint;
fillchar(can,sizeof(can),false);
readln(n,m);
if m<n-1 then
begin
writeln('Cost: -1');
writeln('Cost: -1');
halt;
end;
for i:=1 to m do
readln(x[i],y[i],len[i]);
sort(1,m);
for i:=1 to n do
f[i]:=i;
for i:=1 to m do
union1(x[i],y[i],len[i]);
writeln('Cost: ',ans);
min1:=ans;
for k:=1 to n do
f[k]:=k;
for i:=1 to tt do
begin
fillchar(can,sizeof(can),false);
for k:=1 to n do
f[k]:=k;
ans:=0;
can[pass[i]]:=true;
for j:=1 to m do
union2(x[j],y[j],len[j]);
if ans<min then min:=ans;
end;
if (min=maxlongint)or(min<min1)
then writeln('Cost: -1')
else writeln('Cost: ',min);
end.
基于prim
多开两个数组used记录I,j 两点之间的边是否在最小生成树中。Wmax[I,j]记录i~j在生成树中的路径上权值最大的边。更新原则见代码。
之后，枚举每条不在当前最小生成树中的边map[I,j],加入改变并删除i，j生成树中路径上的最大边wmax[I,j],会得到一棵较小的生成树。再与当前答案比较取小者即可。
If mst+map[I,j]-wmax[I,j]<lessermst then ……
Code
var used:array[1..1000,1..1000] of boolean;
mincost:array[1..1000] of longint;
clos:array[1..1000] of integer;
Wmax:array[1..1000,1..1000] of longint;
map:array[1..1000,1..1000] of longint;
n,m,i,j,k,MST,lesserMST,x,y,z,min:longint;
function max(a,b:longint):longint;
begin
if a>b then exit(a)
else exit(b);
end;
procedure Prim;
begin
for i:=2 to n do
begin
mincost[i]:=map[i,1];
clos[i]:=1;
end;
mincost[1]:=0; clos[1]:=1;
for i:=1 to n-1 do
begin
min:=maxlongint;
for j:=1 to n do
if (mincost[j]<>0)and(mincost[j]<min) then
begin
min:=mincost[j];
k:=j;
end;
inc(MST,min);
used[k,clos[k]]:=true; used[clos[k],k]:=true;
for j:=1 to n do
if mincost[j]=0 then
begin
wmax[j,k]:=max(wmax[j,clos[k]],map[k,clos[k]]);
wmax[k,j]:=wmax[j,k];
end;
mincost[k]:=0;
for j:=1 to n do
if map[k,j]<mincost[j] then
begin
mincost[j]:=map[k,j];
clos[j]:=k;
end;
end;
end;
begin
assign(input,'input.txt'); reset(input);
readln(n,m);
filldword(map,sizeof(map) shr 2,maxlongint shr 1);
for i:=1 to m do
begin
readln(x,y,z);
if z<map[x,y] then
begin
map[x,y]:=z;
map[y,x]:=z;
end;
end;
if m<n-1 then MST:=-1
else Prim;
writeln('Cost: ',MST);
lesserMST:=maxlongint;
for i:=1 to n do
for j:=1 to n do
if (i<>j)and(used[i,j]=false)and(map[i,j]<>maxlongint shr 1) then
if MST+map[i,j]-wmax[i,j]<lesserMST then
lesserMST:=MST+map[i,j]-wmax[i,j];
if lesserMST=maxlongint then
lesserMST:=-1;
writeln('Cost: ',lesserMST);
end.
在次小生成树的问题中，又见到了枚举算法与图结构的结合。
拓扑排序
拓扑排序是有向无环图的序列，可能存在多解。
思想不说，用队列优化：
for i:=1 to n do
if into[i]=0 then
begin
inc(r);
q[r]:=i;
end;
l:=0;
tot:=0;
while l<r do
begin
inc(l);
now:=q[l];
inc(tot);
ans[tot]:=now;
for i:=1 to a[now,0] do
begin
dec(into[a[now,i]]);
if into[a[now,i]]=0 then
begin
inc(r);
q[r]:=a[now,i];
end;
end;
end;
1、 拓扑排序的直接考察
看两个个例题：
例一：【poj 1094】Sorting It All Out
问题
给定多组数据，每组数据中有多个大小关系，让你判断是否能产生一个拓扑序列，如果可以，输出在第几个关系之后得到，并输出这个序列。如果不可以，输出在第几个关系之后无解；如果存在多解，按题目要求输出。
分析
就是拓扑排序，加队列优化，再加一点改进。每次读入关系之后进行拓扑排序。我们知道，如果一个序列能得到拓扑排序的序列，那么在每步有且仅有一个节点的入度为0，如果不存在入度为零的点，则无解。如果入度为零的点的个数多于一个，则存在多解。
对于队列拓扑排序的原理我们了解，每次选取队首元素是，判断当前队伍中元素的个数，如果多于一个，暂时标记多解（可能在后面的过程中出现无解）。那么什么时候队列中不在有元素捏？就是停止while循环的时候，所以我们只需在最后判断是否生成一个长度为n的序列即可（如果存在多解，同样可以生成，想想为什么）。
拓扑排序的关键就是——入度为零的节点！
Code
program liukee;
var
a:array[1..50,0..50] of longint;
into,into1:array[1..50] of longint;
ans:array[1..1000] of longint;
n,m,i,x,y,turn,temp,j:longint;
flag:boolean;
ch1,ch2,kong:char;
function spfa:longint;
var
l,r,now,sum,i,tt:longint;
q:array[1..100000] of longint;
begin
spfa:=1;
fillchar(q,sizeof(q),0);
fillchar(ans,sizeof(ans),0);
l:=0;
r:=0;
tt:=0;
for i:=1 to n do
if into1[i]=0 then
begin
inc(r);
q[r]:=i;
end;
while l<r do
begin
sum:=r-l;
if sum>1 then spfa:=-1;
inc(l);
now:=q[l];
inc(tt);
ans[tt]:=now;
for i:=1 to a[now,0] do
begin
dec(into1[a[now,i]]);
if into1[a[now,i]]=0 then
begin
inc(r);
q[r]:=a[now,i];
end;
end;
end;
if tt<n then exit(0);
end;
begin
readln(n,m);
while (n<>0)and(m<>0)do
begin
flag:=false;
fillchar(a,sizeof(a),0);
fillchar(into,sizeof(into),0);
turn:=0;
for i:=1 to m do
begin
inc(turn);
read(ch1);
x:=ord(ch1)-64;
read(kong);
read(ch2);
readln;
y:=ord(ch2)-64;
inc(a[x,0]);
a[x,a[x,0]]:=y;
inc(into[y]);
if flag then continue;
into1:=into;
temp:=spfa;
if temp=1 then begin write('Sorted sequence determined after ',turn,' relations: ');flag:=true; for j:=1 to n do write(chr(ans[j]+64)); end
else if temp=0 then begin write('Inconsistency found after ',turn,' relations');flag:=true;end;
end;
if not flag then write('Sorted sequence cannot be determined');
readln(n,m);
write('.');
writeln;
end;
end.
例二：frame up
看下面的五张 9 x 8 的图像：
........ ........ ........ ........ .CCC....
EEEEEE.. ........ ........ ..BBBB.. .C.C....
E....E.. DDDDDD.. ........ ..B..B.. .C.C....
E....E.. D....D.. ........ ..B..B.. .CCC....
E....E.. D....D.. ....AAAA ..B..B.. ........
E....E.. D....D.. ....A..A ..BBBB.. ........
E....E.. DDDDDD.. ....A..A ........ ........
E....E.. ........ ....AAAA ........ ........
EEEEEE.. ........ ........ ........ ........
1 2 3 4 5
现在，把这些图像按照 1—5 的编号从下到上重叠，第 1 张在最下面，第 5 张在最顶端。如果一张图像覆盖了另外一张图像，那么底下的图像的一部分就变得不可见了。我们得到下面的图像：
.CCC....
ECBCBB..
DCBCDB..
DCCC.B..
D.B.ABAA
D.BBBB.A
DDDDAD.A
E...AAAA
EEEEEE..
对于这样一张图像，计算构成这张图像的矩形图像从底部到顶端堆叠的顺序。
下面是这道题目的规则：
矩形的边的宽度为 1 ，每条边的长度都不小于 3 。
矩形的每条边中，至少有一部分是可见的。注意，一个角同时属于两条边。
矩形用大写字母表示，并且每个矩形的表示符号都不相同。
[编辑]格式
PROGRAM NAME: frameup
INPUT FORMAT:
(file frameup.in)
第一行 两个用空格分开的整数：图像高 H (3 <= H <=30) 和图像宽 W (3 <= W <= 30) 。
第二行到第 H+1 行 H 行，每行 W 个字母。
OUTPUT FORMAT：
(file frameup.out)
按照自底向上的顺序输出字母。如果有不止一种情况，按照字典顺序输出每一种情况（至少会有一种合法的顺序）。
[编辑] SAMPLE INPUT
9 8
.CCC....
ECBCBB..
DCBCDB..
DCCC.B..
D.B.ABAA
D.BBBB.A
DDDDAD.A
E...AAAA
EEEEEE..
[编辑] SAMPLE OUTPUT
EDABC
分析：
题目的关键条件就是：矩形的每条边都存在可见的部分。也就是说我们可以找到矩形的左下角和右上角。那么我们就可以确定每个矩形的区域。
之后我们审查每个矩形区域里的点，如果存在不是该字母的点，就代表那个字母能覆盖当前字母。如：A字母的区域中出现了字母B，我们就从A到B连一条边。表示b在a的上面。
这样我们就构出了一个图。
之后答案就是改图的拓扑序列，输出每个符合条件的拓扑序列。
拓扑序列不一定只处理大小，具有传递关系的无环关系图都可进行拓扑排序。如此题：a在b上，b在c上，那么a一定在c上。
接下来的问题就是如何输出可能解了。
拓扑排序之所以会多解，就是因为当前入度为零的点不唯一。那么我们就需要把拓扑排序的过程，改成一个深度优先搜索。代码如下：
Procedure outit(t:longint);
Var
I:longint;
Begin
If t=n+1 then
Then begin
Outit;
Exit;
End;
For i:=1 to n do
If into[i]=0 then
If not v[i] then
Begin
For j:=1 to a[I,0] do
Dec(into[a[I,j]]);
V[i]:=true;
Ans[t]:=I;
Dfs(t+1);
V[i]:=false;
For j:=1 to a[I,0] do
Inc(into[a[I,j]]);
End;
End;
Code(略)
2、 拓扑排序用作预处理
拓扑排序往往不会是问题的重点，而是为问题的解决提供一个顺序。或者为动态规划提供一个无后效性的阶段。
看两个例题：
例一：神经网络
1、【2003提高】神经网络(Network)
【问题描述】
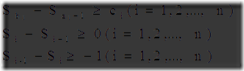
在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经
元之间至多有一条边相连，下图是一个神经元的例子：
公式中的Wji（可能为负值）表示连接j号神经元和 i号神经元的边的权值。当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为Ci。
如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（Ci），要求你的程序运算出最后网络输出层的状态。
【输入格式】
输入文件第一行是两个整数n（1≤n≤200）和p。接下来n行，每行两个整数，第i＋1行是神经元i最初状态和其阈值（Ui），非输入层的神经元开始时状态必然为0。再下面P行，每行由两个整数i，j及一个整数Wij，表示连接神经元i、j的边权值为Wij。
【输出格式】
输出文件包含若干行，每行有两个整数，分别对应一个神经元的编号，及其最后的状态，两个整数间以空格分隔。仅输出最后状态大于零的输出层神经元状态，并且按照编号由小到大顺序输出！
若输出层的神经元最后状态均为小于 0，则输出 NULL。
【样例输入】
5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1
【样例输出】
3 1
4 1
5 1
分析：
题目冗长。抓住关键。如题目所述，神经元是分层的，那么我们要计算每个神经元的兴奋值ci，一定要有一定的顺序。这个顺序就是拓扑序列！
按拓扑序列进行模拟，可以看成是二维约束的拓扑排序，对于一个节点入度必须为零，且c值大于零才能去处理它的邻接节点。
注意特殊情况。对于输入神经来说阀值是没有意义的。就是说它的兴奋值不满足公式。而只有输入神经的c不为零。那么对于c=0的c==-u，否则c==c
如果问题存在很强的阶段性，考虑拓扑排序！
Code
program liukeke;
var
c:array[0..205] of longint;
into:array[0..205] of longint;
q:array[0..100000] of longint;
map,a:array[0..205,0..205] of longint;
i,n,p,cc,u,x,y,z,l,r,now:longint;
flag:boolean;
begin
readln(n,p);
for i:=1 to n do
begin
readln(cc,u);
if cc=0 then
c[i]:=-u
else
begin
c[i]:=cc;
inc(r);
q[r]:=i;
end;
end;
for i:=1 to p do
begin
readln(x,y,z);
map[x,y]:=z;
inc(a[x,0]);
a[x,a[x,0]]:=y;
inc(into[y]);
end;
l:=0;
while l<r do
begin
inc(l);
now:=q[l];
for i:=1 to a[now,0] do
begin
inc(c[a[now,i]],map[now,a[now,i]]*c[now]);
dec(into[a[now,i]]);
if (into[a[now,i]]=0)and(c[a[now,i]]>0) then
begin
inc(r);
q[r]:=a[now,i];
end;
end;
end;
flag:=true;
for i:=1 to n do
if (a[i,0]=0) and (c[i]>0) then
begin
flag:=false;
writeln(i,' ',c[i]);
end;
if flag then writeln('NULL');
end.
例二：挖地雷
【问题描述】
在一个地图上有N个地窖（N<=20），每个地窖中埋有一定数量的地雷。同时，给出地窖之间的连接路径。如图3
图3
当地窖及其连接的数据给出之后，某人可以从任一处开始挖地雷，然后可以沿着指出的连接往下挖（仅能选择一条路径），当无连接时挖地雷工作结束。设计一个挖地雷的方案，使某人能挖到最多的地雷。
【输入文件】
N： （表示地窖的个数）
Ｗ1，W2，W3，……WN （表示每个地窖中埋藏的地雷数量）
A12…………… . A1N 地窖之间连接路径（其中Ａij=1表示地窖i,j
A23…………..A2N 之间是否有通路：通Aij=1,不通Aij==0）
……..
AN-1 AN
【输出文件】
K1--K2--……….KV （挖地雷的顺序）
MAX （挖地雷的数量）
【输入样例】
5
10，8，4，7，6
1 1 1 0
0 0 0
1 1
1
【输出样例】
1 -> 3 -> 4 -> 5
max=27
【Hint】
题目中的路径是有向的且无环路（这是我做的改动原题中没有要求）。
分析
贪心是不行的。可以用动态规划解决。但是本题的阶段不是很明显。怎么样能满足无后效性呢？拓扑排序。有向图中的动态规划一般以拓扑排序作为阶段，因为拓扑序列中靠后的节点不会走到拓扑序列中考前的点，满足无后效性
之后就变成了最长……型动态规划问题了。
Code（略）
最短路
这是图论中最为精髓的部分了。
先介绍三种适用范围不同的常用算法：
Dijkstra算法。这个算法可以求出图中某一个点到其它所有点的最短距离以及路径，但前提是图中没有权为负的边。它的大致思路是：每次找到当前距离最短的一个点，将它的距离固定下来，并用这个距离更新它的邻接点的距离，直至所有点的距离都被固定。采用最朴素实现的Dijkstra的时间复杂度是Θ(n^2)。有一种高效的实现方法是使用一个最小堆保存所有顶点的当前距离，但这造成了需要更新当前距离时的不便，导致了实际中编程的复杂性，一般不考虑使用，点数较少的时候使用。
SPFA算法。（我不打算提Bellman-Ford算法，因为完全可以把SPFA当作Bellman-Ford的一种优化、变形以及竞赛中的替代品。）同样是用来解决单源最短路，图中可以有负权的边。使用一个队列，首先使源点入队，然后每次出队一个顶点，用这个顶点的当前距离更新它的所有邻接点的距离，所有距离实际上被更新且未在队列中的点入队。重复以上过程直至队列空。另外，当一个点入队次数超过图的顶点数时，表明图中存在负权环。SPFA的最坏情况，也就是图中有负权环时的时间复杂度是Θ(n*E)，但在实际应用中若没有负权环时会非常快，甚至可以认为大约与O(E)同阶。我在用到SPFA时一般都采用边表来来存边，这样可以最大限度发挥SPFA的优越性。点数较多而且边数较少时使用。竞赛中使用最频繁，往往考察对spfa算法的改造。或者多约束条件的spfa算法。
Floyd算法可以比较高效地求出图中所有顶点两两之间的最短距离，有负权边也没问题。它的基本思想是枚举每一个顶点，试图用“松弛操作”将它加到最短路径中去。具体的算法不太好用纯语言来描述，所以我就不描述了，保证看代码能一看就懂。它的一大优点是程序非常短且非常不容易写错。所以说，对于一些简单题，图的顶点比较少，特别是在还会有负权边的时候，哪怕需要求的是单源最短路，写一个Floyd也是明智的。Floyd的时间复杂度是雷打不动的Θ(n^3)。常常用作预处理，往往可以对方程进行改造，实现不同的任务要求。
常见的几个应用有：记录路径，记录路径数目，最小环。其他问题则需要具体分析
不管使用什么算法，如果要求得到最短路的具体路径，可以对每个顶点增加一个pre域（在Floyd中，pre需要是一个二维数组），以保存到达这个顶点的最短路的上一个顶点的编号，这样就可以沿着pre提供的信息，逆向找到整条最短路。
在题目中体会吧：
问题
Description
年轻的探险家来到了一个印第安部落里。在那里他和酋长的女儿相爱了，于是便向酋长去求亲。酋长要他用10000个金币作为聘礼才答应把女儿嫁给他。探险家拿不出这么多金币，便请求酋长降低要求。酋长说："嗯，如果你能够替我弄到大祭司的皮袄，我可以只要8000金币。如果你能够弄来他的水晶球，那么只要5000金币就行了。"探险家就跑到大祭司那里，向他要求皮袄或水晶球，大祭司要他用金币来换，或者替他弄来其他的东西，他可以降低价格。探险家于是又跑到其他地方，其他人也提出了类似的要求，或者直接用金币换，或者找到其他东西就可以降低价格。不过探险家没必要用多样东西去换一样东西，因为不会得到更低的价格。探险家现在很需要你的帮忙，让他用最少的金币娶到自己的心上人。另外他要告诉你的是，在这个部落里，等级观念十分森严。地位差距超过一定限制的两个人之间不会进行任何形式的直接接触，包括交易。他是一个外来人，所以可以不受这些限制。但是如果他和某个地位较低的人进行了交易，地位较高的的人不会再和他交易，他们认为这样等于是间接接触，反过来也一样。因此你需要在考虑所有的情况以后给他提供一个最好的方案。
为了方便起见，我们把所有的物品从1开始进行编号，酋长的允诺也看作一个物品，并且编号总是1。每个物品都有对应的价格P，主人的地位等级L，以及一系列的替代品Ti和该替代品所对应的"优惠"Vi。如果两人地位等级差距超过了M，就不能"间接交易"。你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。
Input
输入第一行是两个整数M，N（1 <= N <= 100），依次表示地位等级差距限制和物品的总数。接下来按照编号从小到大依次给出了N个物品的描述。每个物品的描述开头是三个非负整数P、L、X（X < N），依次表示该物品的价格、主人的地位等级和替代品总数。接下来X行每行包括两个整数T和V，分别表示替代品的编号和"优惠价格"。
Output
输出最少需要的金币数。
Sample Input
1 4
10000 3 2
2 8000
3 5000
1000 2 1
4 200
3000 2 1
4 200
50 2 0
Sample Output
5250
分析
首先是构图。将每件物品看成一个节点。将替换物品后的价钱看成边上的权值。但是每个点自身仍有权值，对于这个问题，采取虚拟节点的方法。虚拟0节点，该节点到各点的距离为各物品自身的价值。这样问题就转化成了从0~1的最短路。
还有一个问题就是等级。由于数据范围很小。我们采用枚举的方法，枚举等级区间（区间左端点+等级差距）即可。之后用spfa求最短路即可。
虚拟节点的思想很重要，而长长解决节点本身有价值的问题，将点上的价值全部转化到边上。
枚举能解决，就不要考虑高深的算法！
Code
program liukee;
var
a:array[0..100,0..100] of longint;
map:array[0..100,0..100] of longint;
dj,d:array[0..100] of longint;
v:array[0..100000] of boolean;
q:array[0..100000] of longint;
n,m:longint;
low,high,min:longint;
procedure init;
var
i,j,y,yy,p,l,x:longint;
begin
readln(m,n);
for i:=1 to n do
begin
readln(p,l,x);
dj[i]:=l;
inc(a[0,0]);
a[0,a[0,0]]:=i;
map[0,i]:=p;
for j:=1 to x do
begin
readln(y,yy);
inc(a[y,0]);
a[y,a[y,0]]:=i;
map[y,i]:=yy;
end;
end;
end;
procedure spfa;
var
i,l,r,now:longint;
begin
for i:=1 to n do d[i]:=maxlongint>>1;
l:=0;
r:=1;
q[1]:=0;
v[0]:=true;
while l<r do
begin
inc(l);
now:=q[l];
v[now]:=false;
for i:=1 to a[now,0] do
if (d[a[now,i]]>d[now]+map[now,a[now,i]])and(dj[a[now,i]]>=low)and(dj[a[now,i]]<=high)then
begin
d[a[now,i]]:=d[now]+map[now,a[now,i]];
if not(v[a[now,i]])then
begin
inc(r);
q[r]:=a[now,i];
v[q[r]]:=true;
end;
end;
end;
end;
begin
init;
min:=maxlongint;
for low:=dj[1]-m to dj[1] do
begin
high:=low+m;
if high<dj[1] then continue;
spfa;
if d[1]<>maxlongint>>1 then
if d[1]<min then min:=d[1];
end;
writeln(min);
end.
例二：currency change
问题
Description
一些货币兑换点正在我们的城市工作。我们假设每个兑换点尤其擅长兑换两种特定的货币，并且只进行对这些货币的兑换。可能有一些兑换点专门兑换相同的货币对。每个兑换点都有自己的汇率，货币A到货币B的汇率是你用1货币A换到的货币B的数量。每个兑换点也有一些佣金，即为你需要为你的兑换行动支付的金额。佣金总是从源货币扣除。
例如，如果你想要在汇率为29.75，并且佣金为0.39的兑换点将100美元兑换成俄罗斯卢布，你将会得到（100-0.39）*29.75=2963.3975卢布。
你有N种不同的货币可以在我们的城市进行兑换。我们为每一种货币制定从1到N的唯一一个整数。每个兑换点可以用6个数字形容：整数A和B——它交换的货币（表示为货币A和货币B）；实数RAB，CAB，RBA和CBA——当它分别将货币A兑换成货币B和将货币B兑换成货币A时的汇率和佣金。
叫兽有一定数量的货币S，并且它希望它能以某种方式在一些兑换行动后增加它的资本。最后它的资金必须兑换为货币S。
帮助它解决这个棘手的问题。叫兽在进行它的兑换行动时资金总数必须始终非负。
Input
输入的第一行包含四个数字：N – 货币的数量，M – 兑换点的数量，S – 叫兽具有的货币种类，V – 叫兽具有的货币数量。
下面的M行每行包括6个数字 – 对相应的兑换点的描述。数字相隔一个或多个空格。1<=S<=N<=100，1<=M<=100，V是实数，0<=V<=10^3。
对于每个兑换点汇率和佣金都是实数，小数点后最多有两位小数。10^-2<=汇率<=10^2，0<=佣金<=10^2。
如果在一组兑换行动中没有兑换点被超过一次地使用，我们认为这组兑换行动是简单的。你可以认为最终数值和最初任何一个简单的兑换行动组的比例小于10^4。
Output
如果叫兽能增加它的财产，输出YES，否则输出NO。
Sample Input
3 2 1 20.0
1 2 1.00 1.00 1.00 1.00
2 3 1.10 1.00 1.10 1.00
Sample Output
YES
译者：Hzoi2008_叫兽
分析
仔细理解题意，最后是否收益与如何在兑换点之间移动无关，而是和如何通过兑换点兑换货币有关。所以将所有的货币抽象成节点。在读入时，每个兑换点就可以看成是一条边。
显然，在这个图中是存在着环的。
接下来用spfa算法解决问题。
首先需要修改松弛条件，best存兑换成i货币时的最大收益。Spfa算法本质上是对最短路的改造，只要没有负权回路，就不会出现无解的情况。其精髓就是松弛操作。一但对松弛操作进行了更改就要考虑问题的特殊性了。
对这道题来说，只要多次松弛之后，出现原点的值大于初始钱数，就说明可以收益。这里一点要跳出，因为再经历一次同样的过程会使原点的值继续变大。
Spfa不一定是求最短路，可能是泛化含义的最短路，注意特殊性。
Code
program liukee;
type lkj=record
next:longint;
a:double;
b:double;
end;
var
a:array[1..100,0..100] of lkj;
visit:array[1..100] of boolean;
tot:array[1..100] of longint;
q:array[1..1000000] of longint;
best:array[1..100] of double;
n,m,st:longint;
sum:double;
procedure init;
var
i,x,y:longint;
a1,b1,a2,b2:double;
begin
readln(n,m,st,sum);
for i:=1 to m do
begin
readln(x,y,a1,b1,a2,b2);
inc(tot[x]);
a[x,tot[x]].next:=y;
a[x,tot[x]].a:=a1;
a[x,tot[x]].b:=b1;
inc(tot[y]);
a[y,tot[y]].next:=x;
a[y,tot[y]].a:=a2;
a[y,tot[y]].b:=b2;
end;
end;
procedure spfa;
var
l,r,i,now:longint;
begin
fillchar(visit,sizeof(visit),0);
fillchar(q,sizeof(q),0);
l:=0;r:=1;
for i:=1 to n do best[i]:=-maxlongint;
best[st]:=sum;
q[1]:=st;
visit[st]:=true;
while l<r do
begin
inc(l);
now:=q[l];
visit[now]:=false;
for i:=1 to tot[now] do
if best[a[now,i].next]<(best[now]-a[now,i].b)*a[now,i].a then
begin
best[a[now,i].next]:=(best[now]-a[now,i].b)*a[now,i].a;
if best[st]>sum then
begin
writeln('YES');
exit;
end;
if not visit[a[now,i].next] then
begin
inc(r);
q[r]:=a[now,i].next;
visit[q[r]]:=true;
end;
end;
end;
writeln('NO');
end;
begin
init;
spfa;
end.
例三：Wormholes
问题
就是在求图中有无负权回路。
分析
下面解释一下spfa算法判断负权回路的原理：
我们都知道spfa算法是对bellman算法的优化，那么如何用spfa算法来判断负权回路呢？我们考虑一个节点入队的条件是什么，只有那些在前一遍松弛中改变了距离估计值的点，才可能引起他们的邻接点的距离估计值的改变。因此，用一个先进先出的队列来存放被成功松弛的顶点。同样，我们有这样的定理：“两点间如果有最短路，那么每个结点最多经过一次。也就是说，这条路不超过n-1条边。”（如果一个结点经过了两次，那么我们走了一个圈。如果这个圈的权为正，显然不划算；如果是负圈，那么最短路不存在；如果是零圈，去掉不影响最优值）。也就是说，每个点最多入队n-1次（这里比较难理解，需要仔细体会，n-1只是一种最坏情况，实际中，这样会很大程度上影响程序的效率）。
实际上就是说一个点最多被其他的每个点松弛一次并且入队。
有了上面的基础，思路就很显然了，加开一个数组记录每个点入队的次数（turn），然后，判断当前入队的点的入队次数，如果大于n-1，则说明存在负权回路。
Code
program liukee;
var
a:array[1..1000,0..1000] of longint;
way:array[1..1000,0..1000] of longint;
v:array[1..1000] of boolean;
q:array[1..100000] of longint;
d,turn:array[1..1000] of longint;
zu,n,m,w,i:longint;
procedure init;
var
i,x,y,z:longint;
begin
readln(n,m,w);
for i:=1 to m do
begin
readln(x,y,z);
inc(a[x,0]);
inc(way[x,0]);
a[x,a[x,0]]:=y;
way[x,way[x,0]]:=z;
inc(a[y,0]);
inc(way[y,0]);
a[y,a[y,0]]:=x;
way[y,way[y,0]]:=z;
end;
for i:=1 to w do
begin
readln(x,y,z);
inc(a[x,0]);
inc(way[x,0]);
a[x,a[x,0]]:=y;
way[x,way[x,0]]:=-z;
end;
end;
procedure spfa;
var
l,r,i,now:longint;
begin
l:=0;
r:=1;
for i:=1 to n do d[i]:=maxlongint;
q[1]:=1;
d[1]:=0;
turn[1]:=1;
while l<r do
begin
inc(l);
now:=q[l];
v[now]:=false;
for i:=1 to a[now,0] do
if d[a[now,i]]>d[now]+way[now,i] then
begin
d[a[now,i]]:=d[now]+way[now,i];
if not(v[a[now,i]]) then
begin
inc(r);
inc(turn[a[now,i]]);
q[r]:=a[now,i];
v[q[r]]:=true;
if turn[a[now,i]]>n then
begin
writeln('YES');
exit;
end;
end;
end;
end;
writeln('NO');
end;
begin
readln(zu);
for i:=1 to zu do
begin
fillchar(a,sizeof(a),0);
fillchar(v,sizeof(v),false);
fillchar(q,sizeof(q),0);
fillchar(turn,sizeof(turn),0);
fillchar(way,sizeof(way),0);
fillchar(d,sizeof(d),0);
init;
spfa;
end;
end.
例四：乘车路线（roads.exe）
编号为1.. N的N座城镇用若干仅供单向行驶的道路相连，每条道路上均有两个参数：道路长度(length)和在该条道路上行驶的费用（cost）。BOB准备从城镇1出发到达城镇N，但他目前只有W的钱，为此，你需要帮助他寻找一条从城镇1到城镇N在他能支付的前提下的一条最短路线。
输入：
N K W（N为城镇数目，2<=N<=100，K为道路条数，1<=K<=10000,W为钱的数目，0<=w<=1000）
随后的K行每行为一条道路的信息，包含4个数值（S,D,L,T）其中S为源城镇，D为目标城镇，L为道路长度，T为所需支付用。（1<=S,D<=N,1<=L<=100,0<=T<=100）
输出：
输出最短长度，若无解，则输出“NO”；
分析
典型的二维最短路问题。这里的最短路多了一个约束条件，这个约束条件可以是任意的，比如：经过的路径数目，路径上的最大边，花费限制，必须经过的节点，访问过的节点情况……
依然可以用spfa解决，但是要用二维状态描述。
拿这道题距离d[x,cost]表示从源点到x，花费为cost时的最短路。同理q和v数组同样是二维状态。
只需修改松弛条件：
D[p^.dot,costnow+p^.cost]:=d[now,costnow]+p^.len
最后在cost符合条件的区间找最短路即可。
该造松弛条件，并不影响spfa算法的正确性。可以这么理解：第二维相当于枚举了约束条件。
有几维价值就枚举几维。
此时的时间复杂度不好估计。与邻接表的大小有关，但明显看出松弛和入队的次数都增长了很多。可以认为是o(k*e)k是一个较大的常数。
Code
type pointer=^rec;
rec=record
dot,len,cost:longint;
next:pointer;
end;
var
q1,q2:array[0..1000000] of longint;
d:array[0..101,0..1000] of longint;
v:array[0..101,0..1000] of boolean;
link:array[0..101] of pointer;
p:pointer;
n,m,w,x,y,z1,z2,l,r,now1,now2,ans,i:longint;
begin
assign(input,'roads.in');reset(input);
assign(output,'roads.ou');rewrite(output);
readln(w);
readln(n);
readln(m);
for i:=1 to m do
begin
readln(x,y,z1,z2);
new(p);
p^.dot:=y;
p^.len:=z1;
p^.cost:=z2;
p^.next:=link[x];
link[x]:=p;
end;
l:=0;r:=1;
q1[1]:=1;
q2[1]:=0;
filldword(d,sizeof(d)>>2,maxlongint>>1);
v[1,0]:=true;
d[1,0]:=0;
while l<r do
begin
inc(l);
now1:=q1[l];
now2:=q2[l];
p:=link[now1];
v[now1,now2]:=false;
while p<>nil do
begin
if now2+p^.cost<=w then
begin
if d[p^.dot,now2+p^.cost]>d[now1,now2]+p^.len then
begin
d[p^.dot,now2+p^.cost]:=d[now1,now2]+p^.len;
if not v[p^.dot,now2+p^.cost] then
begin
inc(r);
v[p^.dot,now2+p^.cost]:=true;
q1[r]:=p^.dot;
q2[r]:=now2+p^.cost;
end;
end;
end;
p:=p^.next;
end;
end;
ans:=maxlongint>>1;
for i:=0 to w do
if d[n,i]<ans then ans:=d[n,i];
if ans=maxlongint>>1 then
writeln('NO')
else writeln(ans);
close(input);
close(output);
end.
上面介绍主要是spfa算法的直接应用和变形使用。在竞赛中spfa还是应用最多的算法。一定要深刻理解。Dijistra的局限性较大，不再介绍，但是点数较少的稠密图dij还是不错的选择。
对于单源最短路的spfa算法，仍然有两个地方需要注意：
1、 单源最短路等于边反向之后的单汇最短路
2、 在求多源最短路时，如果是稀疏图，还是spfa较快。Floyd的复杂度是雷打不动的。这一方面是优势，另一方面又是局限。
下面介绍floyd算法的应用。
例五：frogger
问题
求任意两点间的路径中路径上最大边的最小值。
分析
多源问题，floyd最简单的改造
F[I,j]:=min(f[I,j],max(f[I,k],f[k,j]))
在改造floyd要注意，该方程是否能满足最优性要求，初值的处理
Code
program liukee;
var
a:array[0..201,0..201] of double;
n,tt:longint;
procedure init;
var
x,y:array[0..202] of double;
i,j:longint;
begin
fillchar(x,sizeof(x),0);
fillchar(y,sizeof(y),0);
for i:=1 to n do
readln(x[i],y[i]);
for i:=1 to n do
for j:=1 to n do
if i<>j then
a[i,j]:=sqrt(sqr(x[i]-x[j])+sqr(y[i]-y[j]));
for i:=1 to n do
for j:=1 to n do
if a[i,j]=0 then a[i,j]:=maxlongint>>1;
end;
function max(a,b:double):double;
begin
if a>b then exit(a) else exit(b);
end;
procedure doit;
var
i,j,k:longint;
begin
for k:=1 to n do
for i:=1 to n do
for j:=1 to n do
if i<>j then
if (k<>i)and(k<>j) then
if a[i,j]>max(a[i,k],a[k,j]) then a[i,j]:=max(a[i,k],a[k,j]);
writeln('Frog Distance = ',a[1,2]:0:3);
writeln;
end;
begin
readln(n);
tt:=0;
while n<>0 do
begin
inc(tt);
fillchar(a,sizeof(a),0);
init;
writeln('Scenario #',tt);
doit;
readln;
readln(n);
end;
end.
看了一道题后大概知道floyd是个什么东西了，但是仅有这些是绝对不够的。改造方程不是随心所欲的，必须符合其最优子结构原理:
所谓最优子结构，就是在图论中，i~j的最短路，一定包含这调路径上所有节点的最短路。很好证明：将i~j的最短路分解：dis[I,j]:=d[I,k1]+d[k1,k2]+d[k2,k3]……
假如有任意一个点对，d不是最短路，那么换成最短路一定会使dis值变小且不影响图的连通性。那么这就与i~j是最短路的前提矛盾了。
由此，得出了floyd算法，其本质是dp。可以理解成三维状态。
F[I,j,k]表示i~j的最短路，其中最短路径上的点必须都属于1~K（注意这里并不包含i，j
两个端点）。由上面的最优子结构原理，我们很容易得出方程。
F[I,j,k]:=min(f[I,j,k],f[I,j,k-1]);k不是这条最短路径上的点
F[I,j,k]:=min(f[I,j,k],f[I,k,k-1]+f[k,j,k-1]);k是这条最短路径上的点
显然，我们把k拿到最外层循环，就可省去一维。
F[I,j]:=min(f[I,j],f[I,k]+f[k,j]);
Floyd的变形往往是求两点间的某种“路径“最小，我们必须先根据floyd的原理（最优
子结构）看看问题是否可以直接dp。同样，用反证法，我们可以证明上面的方程的正确性。
比如上面那道题。我们要求的是路径上最大的权值最小。
明白了这个，来看下面的题：
例六path
问题
keke非常喜欢Dota这款游戏~但是他总是被Dota复杂的地图困扰，有时候甚至会因为地
图太复杂而失去了自己Gank和Farm的节奏。所以他需要你的帮忙。
地图上一共有n个关键位置，每个关键位置有一个关键值Vi，关键位置之间有m条双向
通路，每条通路有其通行值Ci，我们定义两关键位置之间的距离为其间的通路的通行值
加上路径上关键值最大的关键位置（包括起点终点）的关键值。
keke现在有Q个询问，对于每个询问，你需要告诉他a关键位置和b关键位置间的最短离。
数据范围 n<=250
分析
是一个多源最短路问题，根据n，我们能看出是n3的算法。
首先会想，能否直接动归，能写出下面的方程：
f[i,j]:=f[i,k]+f[k,j]-max[i,k]-max[k,j]+maxx(max[i,k],max[k,j]);
仔细分析，这并不满足最优子结构！
所以究竟哪个点作为路径上的最大点，是需要枚举的！但这样的效率是n4
有floyd的原理，我们发现，1~k是阶段，与点的顺序是无关的。如果我们将点上的权值从
小到大排序之后，当循环到k阶段，就能保证a[k]是当前已产生最优路径上最大的。接下来只需在a[i],a[j],a[k]中取大者更新最优值即可。这样就符合了最优子结构。省去了枚举，复杂度为n3
具体实现时由于不需要找最大值，直接做最短路即可。先做最短路，再利用已有的最短路去更新最优值。
Code
program liukeke;
var
a,w:array[0..250] of longint;
hash:array[0..250] of longint;
map,f:array[0..250,0..250] of longint;
n,m,q,i,j,k,x,y:longint;
procedure sort(l,r:longint);
var
i,j,mid,temp:longint;
begin
i:=l;j:=r;
mid:=a[(l+r)>>1];
repeat
while a[i]<mid do inc(i);
while a[j]>mid do dec(j);
if i<=j then
begin
temp:=a[i];a[i]:=a[j];a[j]:=temp;
temp:=w[i];w[i]:=w[j];w[j]:=temp;
inc(i);
dec(j);
end;
until i>j;
if l<j then sort(l,j);
if i<r then sort(i,r);
end;
procedure init;
var
i,x,y,z:longint;
begin
readln(n,m,q);
for i:=1 to n do
begin
readln(a[i]);
w[i]:=i;
end;
sort(1,n);
for i:=1 to n do
hash[w[i]]:=i;
filldword(map,sizeof(map)>>2,maxlongint>>1);
filldword(f,sizeof(f)>>2,maxlongint>>1);
for i:=1 to m do
begin
readln(x,y,z);
x:=hash[x];
y:=hash[y];
if z<map[x,y] then
begin
map[x,y]:=z;
map[y,x]:=map[x,y];
end;
end;
end;
function max(a,b,c:longint):longint;
begin
max:=a;
if b>max then max:=b;
if c>max then max:=c;
end;
begin
assign(input,'path.in');reset(input);
assign(output,'path.out');rewrite(output);
init;
// main;
for k:=1 to n do
begin
for i:=1 to n do
for j:=1 to n do
if map[i,j]>map[i,k]+map[k,j] then
map[i,j]:=map[i,k]+map[k,j];
for i:=1 to n do
for j:=1 to n do
if f[i,j]>map[i,j]+max(a[i],a[j],a[k]) then
f[i,j]:=map[i,j]+max(a[i],a[j],a[k]);
end;
for i:=1 to q do
begin
readln(x,y);
x:=hash[x];
y:=hash[y];
writeln(f[x,y]);
end;
close(input);
close(output);
end.
至于经典的传递闭包，最小环问题就不再说了。
差分约束系统
差分约束系统是数与图的完美结合。关键在于构图，利用了bellman ford（spfa）算法的松弛原理与图中不等式的一致性。
先看一道例题：
例一：
题目描述:给你n个整点区间，这n个整点区间是一个大整点区间的子区间。对于整点区间[a,b]，是这样定义的：区间[a,b]饱含且仅饱含大于等于a，且小于等于b的所有整数，那么称区间[a,b]为整点区间。我们将整点区间[a,b]中的整数抽象为若干个点，我们在这些点上可以放一个元素或者不放元素，再对[a,b]加以限制，比如整点区间[a,b]至少有c个点上放有元素。我们的任务就是求出对于给定的n个整点区间都满足上述限制的情况下，所需的最少元素个数。
输入格式：
第一行一个整数n
第二行到第n+1行，每行三个用空格隔开的整数a，b，c；意义如题目所述。
输出格式：
一行一个整数表示最少的元素个数
输入样例：
5
3 7 3
8 10 3
6 8 1
1 3 1
10 11 1
输出样例：
6
分析:
看到题目中有许多约束条件的最优性问题考虑差分约束系统。我们先将题目中的关系用多个不等式表示出来：
注意，这里只有第一个不等式是不行的，因为区间是连续的，也就是说点与点不是孤立的。
之后，我们考虑如何把满足不等问题的序列转化为最短路问题。
下面考虑bellman ford算法的原理——多次松弛得到最优值。
松弛之后我们能得到这样的不等关系(链表,最短路为例)：
D[p^.dot]<=d[now]+p^.len
好像和上面的不等式没什么关系。
现在我们让松弛后得到的关系和原不等式的关系相一致：
如果把被减数看成到点，减数看成出发点，常数看成边上的权值。
D[p^.dot]-d[now]>=p^.len
D[p^.dot]>=d[now]+P^.len
原不等关系就和松弛条件完全相同了。由此，如果想得到符合条件的s值，实质上就是在求一条从0~n的最长路。
由于松弛之后的关系是有等号的，所以原不等式的关系必须含有等号，如果没有需要改变值使其拥有等号。由原不等式关系得到松弛条件。
Code
program liukeke;
type pointer=^rec;
rec=record
dot,len:longint;
next:pointer;
end;
var
link:array[0..50000] of pointer;
q:array[0..100000] of longint;
v:array[0..50000] of boolean;
d:array[0..50000] of longint;
l,r,n,m,x,y,z,i,now:longint;
p:pointer;
procedure add(x,y,z:longint);
var
p:pointer;
begin
new(p);
p^.dot:=y;
p^.len:=z;
p^.next:=link[x];
link[x]:=p;
end;
begin
assign(input,'interval.in');reset(input);
assign(output,'interval.out');rewrite(output);
readln(m);
n:=0;
for i:=1 to m do
begin
readln(x,y,z);
add(x-1,y,-z);
if y>n then n:=y;
end;
for i:=1 to n do
begin
add(i,i-1,1);
add(i-1,i,0);
end;
for i:=1 to n do d[i]:=(maxlongint>>1);
l:=0;
r:=1;
q[1]:=0;
v[0]:=true;
d[0]:=0;
while l<>r do
begin
inc(l);
if l>100000 then l:=1;
now:=q[l];
p:=link[now];
v[now]:=false;
while p<>nil do
begin
if d[now]+p^.len<d[p^.dot] then
begin
d[p^.dot]:=d[now]+p^.len;
if not v[p^.dot] then
begin
inc(r);
if r>100000 then r:=1;
q[r]:=p^.dot;
v[p^.dot]:=true;
end;
end;
p:=p^.next;
end;
end;
writeln(d[n]);
close(input);
close(output);
end.
那么我们是否能输出满足条件的s序列呢？
答案是肯定的。因为s表示的含义是0~s的元素个数。而最长路之后每个s值都满足了最短路的属性。Si-si-1即可。注意有时方案不是唯一的。
这方面的题有很多，主要难点在构图上。
只要找到了不等式组，就能很快找到松弛的条件了。注意等号，注意松弛后与原题不等式的统一.
欧拉路
欧拉路就是一笔画问题。
主要有两个问题：1、图中是否存在欧拉路2、输出可行的欧拉路（字典序最小，specialjudge）
例题1 colored sticks
问题
Description
You are given a bunch of wooden sticks. Each endpoint of each stick is colored with some color. Is it possible to align the sticks in a straight line such that the colors of the endpoints that touch are of the same color?
Input
Input is a sequence of lines, each line contains two words, separated by spaces, giving the colors of the endpoints of one stick. A word is a sequence of lowercase letters no longer than 10 characters. There is no more than 250000 sticks.
Output
If the sticks can be aligned in the desired way, output a single line saying Possible, otherwise output Impossible.
Sample Input
blue red
red violet
cyan blue
blue magenta
magenta cyan
Sample Output
Possible
分析
首先是构图。将颜色看成节点，将木棍看连接两个节点的边。问题就转化成了判定这个图中是否存在欧拉回路/通路。
判定方法：
先求出每个点的度。
如果该图存在欧拉回路，则图中不存在入度为奇数的点
如果该图存在欧拉通路， 则图中有且仅有两个节点的入度为奇数，在可行的欧拉通路中，一个做起点，另一个做终点。
对颜色的处理，可用hash，也可用字典树。代码用了字典树。
Code
program liukeke;
var
son:array[0..510001,0..26] of longint;
f,into:array[0..510001] of longint;
ch:array[0..100001] of char;
num:array[0..100001] of longint;
i,sum,tot,w,tt,tt1,tt2,ans:longint;
ss,s1:string;
function find(x:longint):longint;
begin
if f[x]=x then exit(x);
f[x]:=find(f[x]);
exit(f[x]);
end;
procedure union(x,y:longint);
var
tt1,tt2:longint;
begin
tt1:=find(x);
tt2:=find(y);
if tt1<>tt2 then
f[tt1]:=tt2;
end;
procedure dfs(t,x:longint);
var
i:longint;
flag:boolean;
begin
flag:=false;
if t=length(ss)+1 then
begin
tt:=num[x];
exit;
end;
for i:=1 to son[x,0] do
if ch[son[x,i]]=ss[t] then
begin
flag:=true;
dfs(t+1,son[x,i]);
end;
if not flag then
begin
while t<=length(ss) do
begin
inc(son[x,0]);
inc(sum);
ch[sum]:=ss[t];
son[x,son[x,0]]:=sum;
x:=sum;
t:=t+1;
if t=length(ss)+1 then
begin
inc(tot);
num[sum]:=tot;
tt:=tot;
end;
end;
end;
end;
begin
for i:=1 to 50001 do
f[i]:=i;
sum:=1;
tot:=0;
while not eof do
begin
readln(s1);
w:=pos(' ',s1);
ss:=copy(s1,1,w-1);
tt:=0;
dfs(1,0);
tt1:=tt;
ss:=copy(s1,w+1,length(s1)-w);
dfs(1,0);
tt2:=tt;
inc(into[tt1]);
inc(into[tt2]);
union(tt1,tt2);
end;
ans:=find(1);
for i:=1 to tot do
if find(i)<> ans then
begin
writeln('Impossible');
halt;
end;
ans:=0;
for i:=1 to tot do
if odd(into[i]) then inc(ans);
if (ans=0)or(ans=2)then
writeln('Possible')
else writeln('Impossible');
end.
例二closed fences
问题
Farmer John每年有很多栅栏要修理。他总是骑着马穿过每一个栅栏并修复它破损的地方。
John是一个与其他农民一样懒的人。他讨厌骑马，因此从来不两次经过一个栅栏。你必须编一个程序，读入栅栏网络的描述，并计算出一条修栅栏的路径，使每个栅栏都恰好被经过一次。John能从任何一个顶点(即两个栅栏的交点)开始骑马，在任意一个顶点结束。
每一个栅栏连接两个顶点，顶点用1到500标号(虽然有的农场并没有500个顶点)。一个顶点上可连接任意多(>=1)个栅栏。所有栅栏都是连通的(也就是你可以从任意一个栅栏到达另外的所有栅栏)。
你的程序必须输出骑马的路径(用路上依次经过的顶点号码表示)。我们如果把输出的路径看成是一个500进制的数，那么当存在多组解的情况下，输出500进制表示法中最小的一个 (也就是输出第一个数较小的，如果还有多组解，输出第二个数较小的，等等)。
输入数据保证至少有一个解。
[编辑]格式
PROGRAM NAME: fence
INPUT FORMAT：
(fence.in)
第1行: 一个整数F(1 <= F <= 1024)，表示栅栏的数目
第2到F+1行: 每行两个整数i, j(1 <= i,j <= 500)表示这条栅栏连接i与j号顶点。
OUTPUT FORMAT：
(fence.out)
输出应当有F+1行，每行一个整数，依次表示路径经过的顶点号。注意数据可能有多组解，但是只有上面题目要求的那一组解是认为正确的。
[编辑] SAMPLE INPUT
9
1 2
2 3
3 4
4 2
4 5
2 5
5 6
5 7
4 6
[编辑] SAMPLE OUTPUT
1
2
3
4
2
5
4
6
5
7
分析
输出字典序最小的欧拉路。
这样的问题有固定的算法。
如果要生成一个欧拉回路有两种方法，一种是输出点的集合，另一种是输出边的集合。二者都是以点作为搜索的对象，思想是枚举一个点相连的边，删掉这条边，对该点相连的下一个节点进行搜索，直到所有边都删完。
对于每个点，当把与它相邻的所有点都完成搜索后将它加入答案队列。如果是边，删完之后就将这条边加入答案队列即可。
如果要求按字典序输出，就从小到大进行压栈，一次加入答案队列后逆序输出即可。
注意一下下面的代码实现方法:
Code
{
ID: liukeke
PROG: fence
LANG: PASCAL
}
program liukeke;
var
ans:array[0..501] of longint;
into:array[0..501] of longint;
a:array[0..501,0..501] of longint;
max,min,m,i,r,start:longint;
procedure init;
var
i,x,y:longint;
begin
readln(m);
for i:=1 to m do
begin
readln(x,y);
if x>max then max:=x;
if y>max then max:=y;
if x<min then min:=x;
if y<min then min:=y;
inc(a[x,y]);
inc(a[y,x]);
inc(into[x]);
inc(into[y]);
end;
end;
procedure find(x:longint);
var
i:longint;
begin
for i:=min to max do
if a[x,i]<>0 then
begin
dec(a[x,i]);
dec(a[i,x]);
find(i);
end;
inc(r);
ans[r]:=x;
end;
begin
min:=maxlongint;
assign(input,'fence.in');reset(input);
assign(output,'fence.out');rewrite(output);
init;
start:=min;
for i:=min to max do
if odd(into[i]) then
begin
start:=i;
break;
end;
find(start);
for i:=r downto 1 do
writeln(ans[i]);
close(input);close(output);
end.
二分图
先明白匹配的定义：一对一。只有问题是二分图模型，而且满足这个条件时才能用二分图匹配，难点主要是在建图上。
记住两个定理：
1、 点集覆盖（用最少的点覆盖图中所有的边）=最大匹配数
2、 最小边集覆盖（用最少的边覆盖图中所有的点）=图中点数-最大匹配数
看两个例题加深一下理解即可：
例一
【poj 3020】Antenna Placement
问题
给定你一个n*m的图，图中有些‘*’点，其他是‘0’点，在每个‘*’点可以建雷达，每个雷达可以覆盖其上下左右四个方向的‘*’点之一，问你最少建多少雷达，可以将这些‘*’点全部覆盖。
分析
二分图，构图，如果我们把每个‘*’点虚拟成一个节点，分布在二分图的两侧。然后，如果两点能相互覆盖，我们就在两点之间连一条边。要求的问题就转化成了，二分图最小边覆盖！
为什么是二分图呢，以为每个点只能覆盖出自身之外的一个节点，这恰好满足匹配的定义。
怎样求解二分图中的最小边覆盖呢。我们知道，一个匹配可以覆盖到2个不同的节点，那么二分图最大匹配覆盖到的节点数=最大匹配数*2。还没有被覆盖到的节点=总共的节点数-最大匹配数*2。所以，二分图最小边覆盖=最大匹配数+总共的节点数-最大匹配数*2=总的的节点数-最大匹配数
例二
问题
给你一个n*n的图，上面有m个需要清楚的障碍，每次可以消除一行或者一列上的障碍物。问你最少用多少次，可以消除图上的所有障碍。
分析
关键是构图，我们将原图抽象成一个二分图：左边是x，右边是y，如果（x，y）上有障碍物，那么就连一条边。我们的任务是消除障碍物，也就是说，用最少的点覆盖图中所有的边！
也就是求二分图的最小点集覆盖！
我们用到一个强大的定理：二分图最小点集覆盖数=最大匹配数，网上有好多证明。
这里大体说一种思路，如果最大匹配的边涉及到的点无法将所有边覆盖，那么当前匹配一定不是最大匹配！
二分图不是noip考察的重点，但是好多题却能用二分图解决。主要难点在于抽象出二分图的模型，至于匈牙利算法，不是问题。
总结
基本思想都已涵盖，剩下的就是积累与临场的发挥了。
