LSTM的推导与实现

LSTM的推导与实现

前言

最近在看CS224d，这里主要介绍LSTM(Long Short-Term Memory)的推导过程以及用Python进行简单的实现。LSTM是一种时间递归神经网络，是RNN的一个变种，非常适合处理和预测时间序列中间隔和延迟非常长的事件。假设我们去试着预测‘I grew up in France...（很长间隔）...I speak fluent French’最后的单词，当前的信息建议下一个此可能是一种语言的名字（因为speak嘛），但是要准确预测出‘French’我们就需要前面的离当前位置较远的‘France’作为上下文，当这个间隔比较大的时候RNN就会难以处理，而LSTM则没有这个问题。

LSTM的原理

为了弄明白LSTM的实现，我下载了alex的原文，但是被论文上图片和公式弄的晕头转向，无奈最后在网上收集了一些资料才总算弄明白。我这里不介绍就LSTM的前置RNN了，不懂的童鞋自己了解一下吧。

LSTM的前向过程

首先看一张LSTM节点的内部示意图：

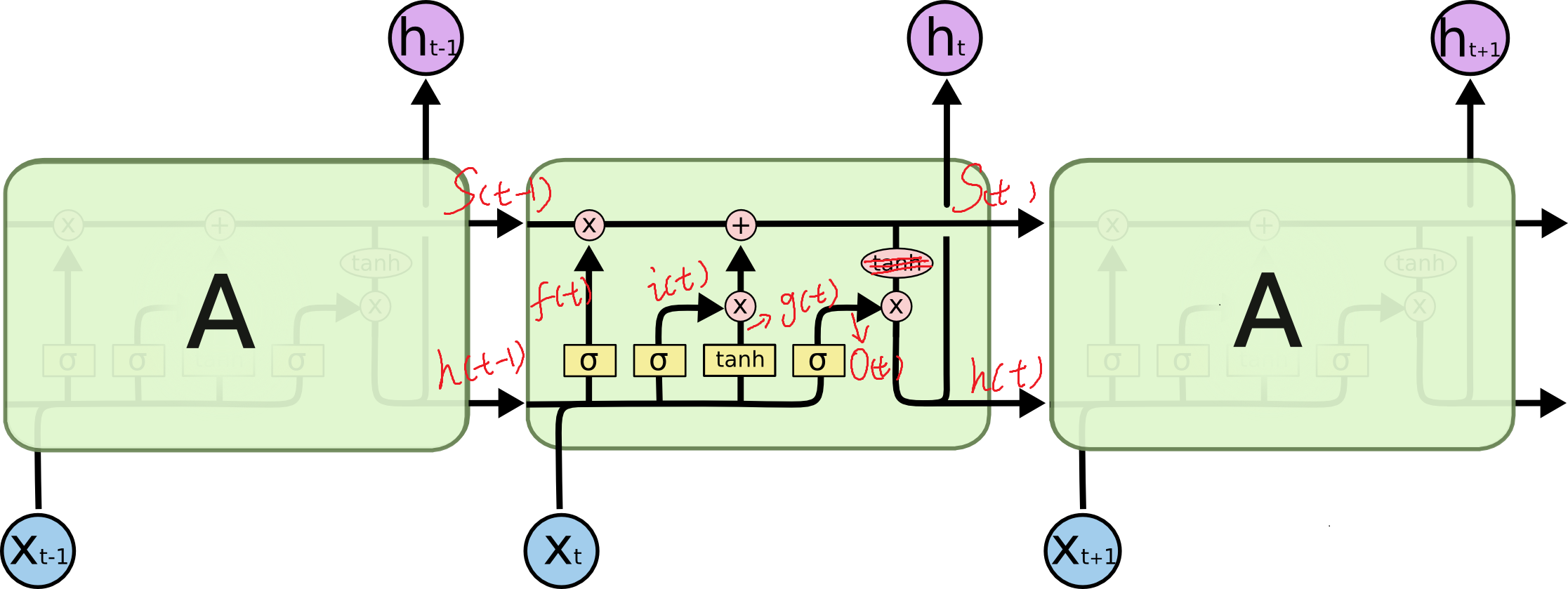
图片来自一篇讲解LSTM的blog(http://colah.github.io/posts/2015-08-Understanding-LSTMs/)
这是我认为网上画的最好的LSTM网络节点图（比论文里面画的容易理解多了），LSTM前向过程就是看图说话，关键的函数节点已经在图中标出,这里我们忽略了其中一个tanh计算过程。

\[\begin{eqnarray} g(t) &=& \phi(W_{gx}x(t) + W_{gh}h(t-1) + b_{g} \\ i(t) &=& \sigma(W_{ix}x(t) + W_{ih}h(t-1) + b_{i} \\ f(t) &=& \sigma(W_{fx}x(t) + W_{fh}h(t-1) + b_{f} \\ o(t) &=& \sigma(W_{ox}x(t) + W_{oh}h(t-1) + b_{o} \\ s(t) &=& g(t)*i(t) + s(t-1)*f(t) \\ h(t) &=& s(t) * o(t) \end{eqnarray} \]

这里\(\phi(x)=tanh(x),\sigma(x)=\frac{1}{1+e^{-x}}\)，\(x(t),h(t)\)分别是我们的输入序列和输出序列。如果我们把\(x(t)\)与\(h(t-1)\)这两个向量进行合并:

\[x_c(t)=[x(t),h(t-1)] \]

那么可以上面的方程组可以重写为:

\[\begin{eqnarray} g(t) &=& \phi(W_{g}x_c(t)) + b_{g} \\ i(t) &=& \sigma(W_{i}x_c(t)) + b_{i} \\ f(t) &=& \sigma(W_{f}x_c(t)) + b_{f} \\ o(t) &=& \sigma(W_{o}x_c(t)) + b_{o} \\ s(t) &=& g(t)*i(t) + s(t-1)*f(t) \\ h(t) &=& s(t) * o(t) \end{eqnarray} \]

其中\(f(t)\)被称为忘记门，所表达的含义是决定我们会从以前状态中丢弃什么信息。\(i(t),g(t)\)构成了输入门，决定什么样的新信息被存放在细胞状态中。\(o(t)\)所在位置被称作输出门，决定我们要输出什么值。这里表述的不是很准确，感兴趣的读者可以去http://colah.github.io/posts/2015-08-Understanding-LSTMs/ NLP这块我也不太懂。

前向过程的代码如下：

def bottom_data_is(self, x, s_prev = None, h_prev = None):
        # if this is the first lstm node in the network
        if s_prev == None: s_prev = np.zeros_like(self.state.s)
        if h_prev == None: h_prev = np.zeros_like(self.state.h)
        # save data for use in backprop
        self.s_prev = s_prev
        self.h_prev = h_prev

        # concatenate x(t) and h(t-1)
        xc = np.hstack((x,  h_prev))
        self.state.g = np.tanh(np.dot(self.param.wg, xc) + self.param.bg)
        self.state.i = sigmoid(np.dot(self.param.wi, xc) + self.param.bi)
        self.state.f = sigmoid(np.dot(self.param.wf, xc) + self.param.bf)
        self.state.o = sigmoid(np.dot(self.param.wo, xc) + self.param.bo)
        self.state.s = self.state.g * self.state.i + s_prev * self.state.f
        self.state.h = self.state.s * self.state.o
        self.x = x
        self.xc = xc

LSTM的反向过程

LSTM的正向过程比较容易，反向过程则比较复杂，我们先定义一个loss function \(l(t)=f(h(t),y(t)))=||h(t)-y(t)||^2\)，\(h(t),y(t)\)分别为输出序列与样本标签，我们要做的就是最小化整个时间序列上的\(l(t)\)，即最小化

\[L=\sum_{t=1}^{T}l(t) \]

其中\(T\)代表整个时间序列，下面我们通过\(L\)来计算梯度，假设我们要计算\(\frac{dL}{dw}\)，其中\(w\)是一个标量(例如是矩阵\(W_{gx}\)的一个元素)，由链式法则可以导出

\[\frac{dL}{dw} = \sum_{t=1}^{T}\sum_{i=1}^{M}\frac{dL}{dh_i(t)}\frac{dh_i(t)}{dw} \]

其中\(h_i(t)\)是第i个单元的输出，\(M\)是LSTM单元的个数，网络随着时间t前向传播，\(h_i(t)\)的改变不影响t时刻之前的loss，我们可以写出：

\[\frac{dL}{dh_i(t)} = \sum_{s=1}^{T}\frac{dl(s)}{dh_i(t)} = \sum_{s=t}^{T}\frac{dl(s)}{dh_i(t)} \]

为了书写方便我们令\(L(t)=\sum_{s=t}^{T}l(s)\)来简化我们的书写，这样\(L(1)\)就是整个序列的loss，重写上式有：

\[\frac{dL}{dh_i(t)} = \sum_{s=1}^{T}\frac{dl(s)}{dh_i(t)} = \frac{dL(t)}{dh_i(t)} \]

这样我们就可以将梯度重写为：

\[\frac{dL}{dw} = \sum_{t=1}^{T}\sum_{i=1}^{M}\frac{dL(t)}{dh_i(t)}\frac{dh_i(t)}{dw} \]

我们知道\(L(t)=l(t)+L(t+1)\)，那么\(\frac{dL(t)}{dh_i(t)}=\frac{dl(t)}{dh_i(t)} + \frac{dL(t+1)}{dh_i(t)}\)，这说明得到下一时序的导数后可以直接得出当前时序的导数，所以我们可以计算\(T\)时刻的导数然后往前推，在\(T\)时刻有\(\frac{dL(T)}{dh_i(T)}=\frac{dl(T)}{dh_i(T)}\)。

def y_list_is(self, y_list, loss_layer):
        """
        Updates diffs by setting target sequence
        with corresponding loss layer.
        Will *NOT* update parameters.  To update parameters,
        call self.lstm_param.apply_diff()
        """
        assert len(y_list) == len(self.x_list)
        idx = len(self.x_list) - 1
        # first node only gets diffs from label ...
        loss = loss_layer.loss(self.lstm_node_list[idx].state.h, y_list[idx])
        diff_h = loss_layer.bottom_diff(self.lstm_node_list[idx].state.h, y_list[idx])
        # here s is not affecting loss due to h(t+1), hence we set equal to zero
        diff_s = np.zeros(self.lstm_param.mem_cell_ct)
        self.lstm_node_list[idx].top_diff_is(diff_h, diff_s)
        idx -= 1

        ### ... following nodes also get diffs from next nodes, hence we add diffs to diff_h
        ### we also propagate error along constant error carousel using diff_s
        while idx >= 0:
            loss += loss_layer.loss(self.lstm_node_list[idx].state.h, y_list[idx])
            diff_h = loss_layer.bottom_diff(self.lstm_node_list[idx].state.h, y_list[idx])
            diff_h += self.lstm_node_list[idx + 1].state.bottom_diff_h
            diff_s = self.lstm_node_list[idx + 1].state.bottom_diff_s
            self.lstm_node_list[idx].top_diff_is(diff_h, diff_s)
            idx -= 1

        return loss

从上面公式可以很容易理解diff_h的计算过程。这里的loss_layer.bottom_diff定义如下：

def bottom_diff(self, pred, label):
        diff = np.zeros_like(pred)
        diff[0] = 2 * (pred[0] - label)
        return diff

该函数结合上文的loss function很明显。下面来推导\(\frac{dL(t)}{ds(t)}\)，结合前面的前向公式我们可以很容易得出\(s(t)\)的变化会直接影响\(h(t)\)和\(h(t+1)\)，进而影响\(L(t)\)，即有：

\[\frac{dL(t)}{dh_i(t)}=\frac{dL(t)}{dh_i(t)}*\frac{dh_i(t)}{ds_i(t)} + \frac{dL(t)}{dh_i(t+1)}*\frac{dh_i(t+1)}{ds_i(t)} \]

因为\(h(t+1)\)不影响\(l(t)\)所以有\(\frac{dL(t)}{dh_i(t+1)}=\frac{dL(t+1)}{dh_i(t+1)}\)，因此有：

\[\frac{dL(t)}{dh_i(t)}=\frac{dL(t)}{dh_i(t)}*\frac{dh_i(t)}{ds_i(t)} + \frac{dL(t+1)}{dh_i(t+1)}*\frac{dh_i(t+1)}{ds_i(t)}=\frac{dL(t)}{dh_i(t)}*\frac{dh_i(t)}{ds_i(t)} + \frac{dL(t+1)}{ds_i(t)} \]

同样的我们可以通过后面的导数逐级反推得到前面的导数，代码即diff_s的计算过程。

下面我们计算\(\frac{dL(t)}{dh_i(t)}*\frac{dh_i(t)}{ds_i(t)}\)，因为\(h(t)=s(t)*o(t)\)，那么\(\frac{dL(t)}{dh_i(t)}*\frac{dh_i(t)}{ds_i(t)}=\frac{dL(t)}{dh_i(t)}*o_i(t)=o_i(t)[diff\_h]\)，即\(\frac{dL(t)}{ds_i(t)}=o(t)[diff\_h]_i+[diff\_s]_i\)，其中\([diff\_h]_i,[diff\_s]_i\)分别表述当前t时序的\(\frac{dL(t)}{dh_i(t)}\)和t+1时序的\(\frac{dL(t)}{ds_i(t)}\)。同样的，结合上面的代码应该比较容易理解。

下面我们根据前向过程挨个计算导数：

\[\begin{eqnarray} \frac{dL(t)}{do(t)}&=&\frac{dL(t)}{dh(t)}*s(t) \\ \frac{dL(t)}{di(t)}&=&\frac{dL(t)}{ds(t)}*\frac{ds(t)}{di(t)}=\frac{dL(t)}{ds(t)}*g(t) \\ \frac{dL(t)}{dg(t)}&=&\frac{dL(t)}{ds(t)}*\frac{ds(t)}{dg(t)}=\frac{dL(t)}{ds(t)}*i(t) \\ \frac{dL(t)}{df(t)}&=&\frac{dL(t)}{ds(t)}*\frac{ds(t)}{df(t)}=\frac{dL(t)}{ds(t)}*s(t-1) \\ \end{eqnarray} \]

因此有以下代码：

def top_diff_is(self, top_diff_h, top_diff_s):
        # notice that top_diff_s is carried along the constant error carousel
        ds = self.state.o * top_diff_h + top_diff_s
        do = self.state.s * top_diff_h
        di = self.state.g * ds
        dg = self.state.i * ds
        df = self.s_prev * ds

        # diffs w.r.t. vector inside sigma / tanh function
        di_input = (1. - self.state.i) * self.state.i * di #sigmoid diff
        df_input = (1. - self.state.f) * self.state.f * df
        do_input = (1. - self.state.o) * self.state.o * do
        dg_input = (1. - self.state.g ** 2) * dg #tanh diff

        # diffs w.r.t. inputs
        self.param.wi_diff += np.outer(di_input, self.xc)
        self.param.wf_diff += np.outer(df_input, self.xc)
        self.param.wo_diff += np.outer(do_input, self.xc)
        self.param.wg_diff += np.outer(dg_input, self.xc)
        self.param.bi_diff += di_input
        self.param.bf_diff += df_input
        self.param.bo_diff += do_input
        self.param.bg_diff += dg_input

        # compute bottom diff
        dxc = np.zeros_like(self.xc)
        dxc += np.dot(self.param.wi.T, di_input)
        dxc += np.dot(self.param.wf.T, df_input)
        dxc += np.dot(self.param.wo.T, do_input)
        dxc += np.dot(self.param.wg.T, dg_input)

        # save bottom diffs
        self.state.bottom_diff_s = ds * self.state.f
        self.state.bottom_diff_x = dxc[:self.param.x_dim]
        self.state.bottom_diff_h = dxc[self.param.x_dim:]

这里top_diff_h，top_diff_s分别是上文的diff_h，diff_s。这里我们讲解下wi_diff的求解过程，其他变量类似。

\[\frac{dL(t)}{dW_i} = \frac{dL(t)}{di(t)}*\frac{di(t)}{d(W_ix_c(t))}*\frac{d(W_ix_c(t))}{dx_c(t)} \]

上式化简之后即得到以下代码

        wi_diff += np.outer((1.-i)*i*di, xc)

其它的导数可以同样得到，这里就不赘述了。

LSTM完整例子

#lstm在输入一串连续质数时预估下一个质数
import random

import numpy as np
import math

def sigmoid(x): 
    return 1. / (1 + np.exp(-x))

# createst uniform random array w/ values in [a,b) and shape args
def rand_arr(a, b, *args): 
    np.random.seed(0)
    return np.random.rand(*args) * (b - a) + a

class LstmParam:
    def __init__(self, mem_cell_ct, x_dim):
        self.mem_cell_ct = mem_cell_ct
        self.x_dim = x_dim
        concat_len = x_dim + mem_cell_ct
        # weight matrices
        self.wg = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len)
        self.wi = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len) 
        self.wf = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len)
        self.wo = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len)
        # bias terms
        self.bg = rand_arr(-0.1, 0.1, mem_cell_ct) 
        self.bi = rand_arr(-0.1, 0.1, mem_cell_ct) 
        self.bf = rand_arr(-0.1, 0.1, mem_cell_ct) 
        self.bo = rand_arr(-0.1, 0.1, mem_cell_ct) 
        # diffs (derivative of loss function w.r.t. all parameters)
        self.wg_diff = np.zeros((mem_cell_ct, concat_len)) 
        self.wi_diff = np.zeros((mem_cell_ct, concat_len)) 
        self.wf_diff = np.zeros((mem_cell_ct, concat_len)) 
        self.wo_diff = np.zeros((mem_cell_ct, concat_len)) 
        self.bg_diff = np.zeros(mem_cell_ct) 
        self.bi_diff = np.zeros(mem_cell_ct) 
        self.bf_diff = np.zeros(mem_cell_ct) 
        self.bo_diff = np.zeros(mem_cell_ct) 

    def apply_diff(self, lr = 1):
        self.wg -= lr * self.wg_diff
        self.wi -= lr * self.wi_diff
        self.wf -= lr * self.wf_diff
        self.wo -= lr * self.wo_diff
        self.bg -= lr * self.bg_diff
        self.bi -= lr * self.bi_diff
        self.bf -= lr * self.bf_diff
        self.bo -= lr * self.bo_diff
        # reset diffs to zero
        self.wg_diff = np.zeros_like(self.wg)
        self.wi_diff = np.zeros_like(self.wi) 
        self.wf_diff = np.zeros_like(self.wf) 
        self.wo_diff = np.zeros_like(self.wo) 
        self.bg_diff = np.zeros_like(self.bg)
        self.bi_diff = np.zeros_like(self.bi) 
        self.bf_diff = np.zeros_like(self.bf) 
        self.bo_diff = np.zeros_like(self.bo) 

class LstmState:
    def __init__(self, mem_cell_ct, x_dim):
        self.g = np.zeros(mem_cell_ct)
        self.i = np.zeros(mem_cell_ct)
        self.f = np.zeros(mem_cell_ct)
        self.o = np.zeros(mem_cell_ct)
        self.s = np.zeros(mem_cell_ct)
        self.h = np.zeros(mem_cell_ct)
        self.bottom_diff_h = np.zeros_like(self.h)
        self.bottom_diff_s = np.zeros_like(self.s)
        self.bottom_diff_x = np.zeros(x_dim)
    
class LstmNode:
    def __init__(self, lstm_param, lstm_state):
        # store reference to parameters and to activations
        self.state = lstm_state
        self.param = lstm_param
        # non-recurrent input to node
        self.x = None
        # non-recurrent input concatenated with recurrent input
        self.xc = None

    def bottom_data_is(self, x, s_prev = None, h_prev = None):
        # if this is the first lstm node in the network
        if s_prev == None: s_prev = np.zeros_like(self.state.s)
        if h_prev == None: h_prev = np.zeros_like(self.state.h)
        # save data for use in backprop
        self.s_prev = s_prev
        self.h_prev = h_prev

        # concatenate x(t) and h(t-1)
        xc = np.hstack((x,  h_prev))
        self.state.g = np.tanh(np.dot(self.param.wg, xc) + self.param.bg)
        self.state.i = sigmoid(np.dot(self.param.wi, xc) + self.param.bi)
        self.state.f = sigmoid(np.dot(self.param.wf, xc) + self.param.bf)
        self.state.o = sigmoid(np.dot(self.param.wo, xc) + self.param.bo)
        self.state.s = self.state.g * self.state.i + s_prev * self.state.f
        self.state.h = self.state.s * self.state.o
        self.x = x
        self.xc = xc
    
    def top_diff_is(self, top_diff_h, top_diff_s):
        # notice that top_diff_s is carried along the constant error carousel
        ds = self.state.o * top_diff_h + top_diff_s
        do = self.state.s * top_diff_h
        di = self.state.g * ds
        dg = self.state.i * ds
        df = self.s_prev * ds

        # diffs w.r.t. vector inside sigma / tanh function
        di_input = (1. - self.state.i) * self.state.i * di 
        df_input = (1. - self.state.f) * self.state.f * df 
        do_input = (1. - self.state.o) * self.state.o * do 
        dg_input = (1. - self.state.g ** 2) * dg

        # diffs w.r.t. inputs
        self.param.wi_diff += np.outer(di_input, self.xc)
        self.param.wf_diff += np.outer(df_input, self.xc)
        self.param.wo_diff += np.outer(do_input, self.xc)
        self.param.wg_diff += np.outer(dg_input, self.xc)
        self.param.bi_diff += di_input
        self.param.bf_diff += df_input       
        self.param.bo_diff += do_input
        self.param.bg_diff += dg_input       

        # compute bottom diff
        dxc = np.zeros_like(self.xc)
        dxc += np.dot(self.param.wi.T, di_input)
        dxc += np.dot(self.param.wf.T, df_input)
        dxc += np.dot(self.param.wo.T, do_input)
        dxc += np.dot(self.param.wg.T, dg_input)

        # save bottom diffs
        self.state.bottom_diff_s = ds * self.state.f
        self.state.bottom_diff_x = dxc[:self.param.x_dim]
        self.state.bottom_diff_h = dxc[self.param.x_dim:]

class LstmNetwork():
    def __init__(self, lstm_param):
        self.lstm_param = lstm_param
        self.lstm_node_list = []
        # input sequence
        self.x_list = []

    def y_list_is(self, y_list, loss_layer):
        """
        Updates diffs by setting target sequence 
        with corresponding loss layer. 
        Will *NOT* update parameters.  To update parameters,
        call self.lstm_param.apply_diff()
        """
        assert len(y_list) == len(self.x_list)
        idx = len(self.x_list) - 1
        # first node only gets diffs from label ...
        loss = loss_layer.loss(self.lstm_node_list[idx].state.h, y_list[idx])
        diff_h = loss_layer.bottom_diff(self.lstm_node_list[idx].state.h, y_list[idx])
        # here s is not affecting loss due to h(t+1), hence we set equal to zero
        diff_s = np.zeros(self.lstm_param.mem_cell_ct)
        self.lstm_node_list[idx].top_diff_is(diff_h, diff_s)
        idx -= 1

        ### ... following nodes also get diffs from next nodes, hence we add diffs to diff_h
        ### we also propagate error along constant error carousel using diff_s
        while idx >= 0:
            loss += loss_layer.loss(self.lstm_node_list[idx].state.h, y_list[idx])
            diff_h = loss_layer.bottom_diff(self.lstm_node_list[idx].state.h, y_list[idx])
            diff_h += self.lstm_node_list[idx + 1].state.bottom_diff_h
            diff_s = self.lstm_node_list[idx + 1].state.bottom_diff_s
            self.lstm_node_list[idx].top_diff_is(diff_h, diff_s)
            idx -= 1 

        return loss

    def x_list_clear(self):
        self.x_list = []

    def x_list_add(self, x):
        self.x_list.append(x)
        if len(self.x_list) > len(self.lstm_node_list):
            # need to add new lstm node, create new state mem
            lstm_state = LstmState(self.lstm_param.mem_cell_ct, self.lstm_param.x_dim)
            self.lstm_node_list.append(LstmNode(self.lstm_param, lstm_state))

        # get index of most recent x input
        idx = len(self.x_list) - 1
        if idx == 0:
            # no recurrent inputs yet
            self.lstm_node_list[idx].bottom_data_is(x)
        else:
            s_prev = self.lstm_node_list[idx - 1].state.s
            h_prev = self.lstm_node_list[idx - 1].state.h
            self.lstm_node_list[idx].bottom_data_is(x, s_prev, h_prev)

测试代码

import numpy as np

from lstm import LstmParam, LstmNetwork

class ToyLossLayer:
    """
    Computes square loss with first element of hidden layer array.
    """
    @classmethod
    def loss(self, pred, label):
        return (pred[0] - label) ** 2

    @classmethod
    def bottom_diff(self, pred, label):
        diff = np.zeros_like(pred)
        diff[0] = 2 * (pred[0] - label)
        return diff

def example_0():
    # learns to repeat simple sequence from random inputs
    np.random.seed(0)

    # parameters for input data dimension and lstm cell count 
    mem_cell_ct = 100
    x_dim = 50
    concat_len = x_dim + mem_cell_ct
    lstm_param = LstmParam(mem_cell_ct, x_dim) 
    lstm_net = LstmNetwork(lstm_param)
    y_list = [-0.5,0.2,0.1, -0.5]
    input_val_arr = [np.random.random(x_dim) for _ in y_list]

    for cur_iter in range(100):
        print "cur iter: ", cur_iter
        for ind in range(len(y_list)):
            lstm_net.x_list_add(input_val_arr[ind])
            print "y_pred[%d] : %f" % (ind, lstm_net.lstm_node_list[ind].state.h[0])

        loss = lstm_net.y_list_is(y_list, ToyLossLayer)
        print "loss: ", loss
        lstm_param.apply_diff(lr=0.1)
        lstm_net.x_list_clear()

if __name__ == "__main__":
    example_0()

参考

略