逻辑回归_吴恩达
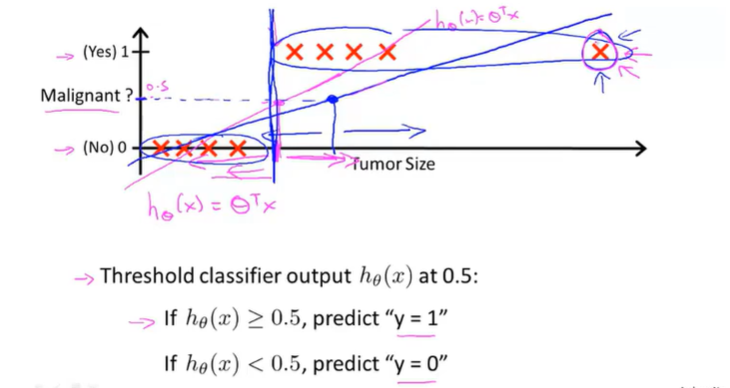
新增最右边额外的红色点,会改变原来的线性回归的拟合直线从洋红改变到蓝色直线,运用原来的数据标准,分类出现了错误,使得新的拟合直线更糟糕
而且分类问题通常只有0和1,但是线性回归会得出小于0或者大于1的值 就很奇怪,但是下面的逻辑回归值一定在【0,1】之间
所以用到了sigmoid function(Logistic function)

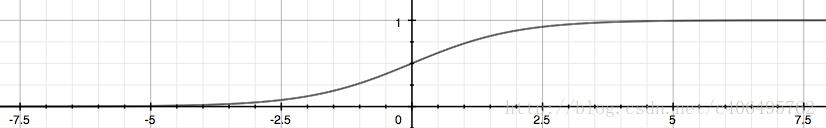
之前线性回归用到的假设函数:(θ和x都是向量)

两者结合起来就变成
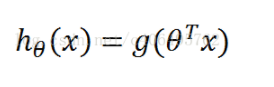
整合成一个公式

使用方法:

在已知样本x和参数θ的情况下,样本x属性正样本(y=1)和负样本(y=0)的条件概率
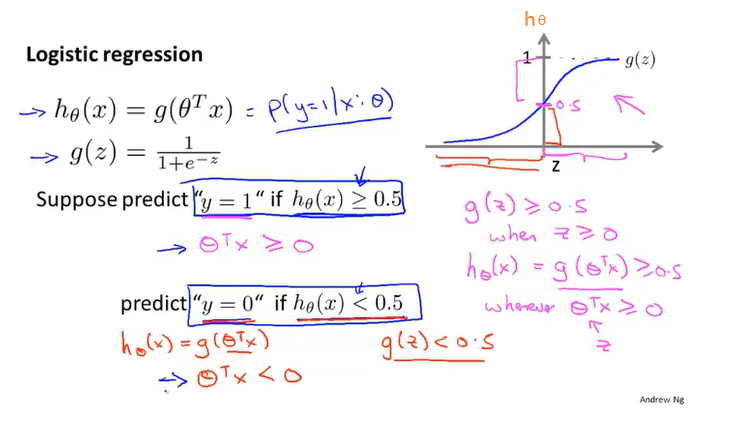
简单分类例子(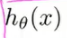 )
)

用训练集来拟合参数θ,然后就确定了决策边界(是假设本身及其参数的属性)
决策边界可以跟随高阶项,得到非常复杂的决策边界
自动选择参数θ

按照之前学习的代价函数,代入sigmoid后,hθ就像左图一样有缺陷,我们目标是得到右图那样,可以使用梯度下降(或者其他)找到全局最优解,所以要稍微改变下原来的函数
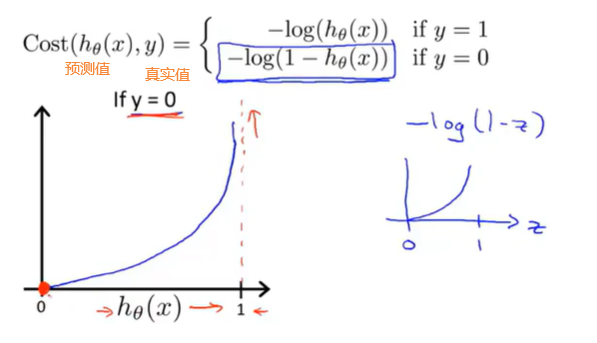

当真实值y=0的时候,预测值为0时候代价小,若是预测值为1的时候代价就很大很大,就会以此来惩罚算法。
现在已知:

将cost函数合并成一个等式:

min最小化后,得到某组拟合训练样本的参数θ,然后用新样本具有某些特征x,和得到的θ来output输出这样的预测(0,1),y=1的概率

要弄清楚如何最小化Jθ: 梯度下降

推导可得:

用向量化可以直接一次把所有的θ全部更新
异:
与线性回归的区别:假设的定义不同。
同:
监测其是否收敛的方法相同。
特征缩放提高梯度下降收敛速度同样试试用
共轭梯度法、BFGS、L-BFGS (直接调库使用)
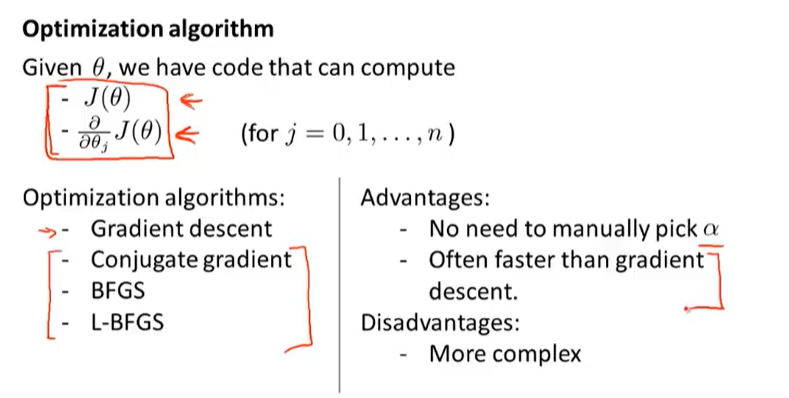
多元分类
(邮件是来自工作,朋友,家人还是其他)
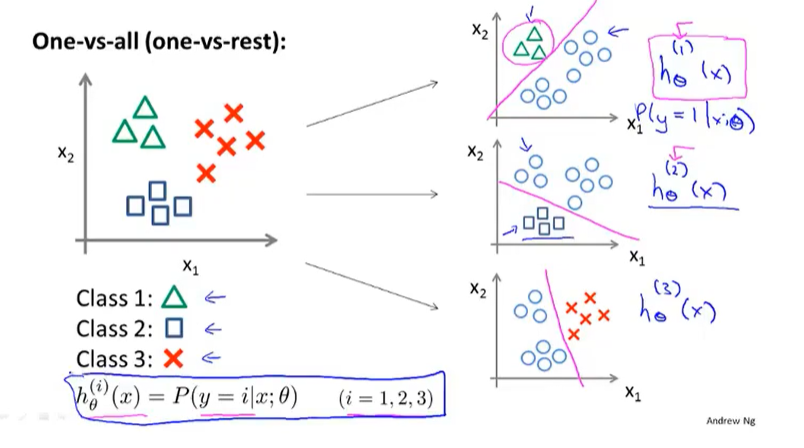
先拟合出X个分类器(每个分类器都针对其中一种情况进行训练)
然后输入新数据x,分别进行预测,取hθ(x)最大的那个





· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 字符编码:从基础到乱码解决
· 提示词工程——AI应用必不可少的技术