【算法题型总结】---7、动态规划

〇、目录

一、套路

二、题型

（一）爬楼梯

1、爬楼梯

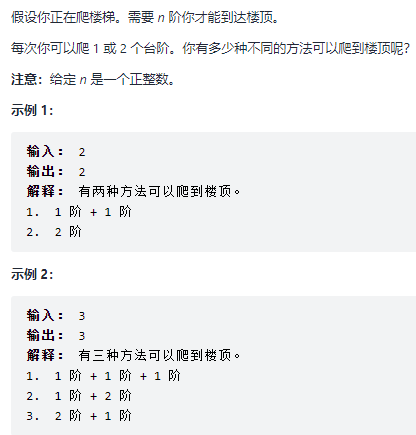
class Solution {
    public int climbStairs(int n) {

    }
}

五部曲：确定数组、确定递推公式、dp数组初始化、确定遍历顺序、举例推导

方法1: 循环/递归

class Solution {
    public int climbStairs(int n) {
        // 跟斐波那契数列一样
        if(n <= 2) return n;
        int a = 1, b = 2, sum = 0;
        
        for(int i = 3; i <= n; i++){
            sum = a + b;
            a = b;
            b = sum;
        }
        return b;
    }
}

方法2:动态规划

// 常规方式
public int climbStairs(int n) {
    int[] dp = new int[n + 1];
    dp[0] = 1;
    dp[1] = 1;
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}
// 用变量记录代替数组
public int climbStairs(int n) {
    int a = 0, b = 1, c = 0; // 默认需要1次
    for (int i = 1; i <= n; i++) {
        c = a + b;          // f(i - 1) + f(n - 2)
        a = b;              // 记录上一轮的值
        b = c;              // 向后步进1个数
    }
    return c;
}

2、使用最小花费爬楼梯

数组的每个下标作为一个阶梯，第 i 个阶梯对应着一个非负数的体力花费值 cost[i]（下标从 0 开始）。

每当你爬上一个阶梯你都要花费对应的体力值，一旦支付了相应的体力值，你就可以选择向上爬一个阶梯或者爬两个阶梯。

请你找出达到楼层顶部的最低花费。在开始时，你可以选择从下标为 0 或 1 的元素作为初始阶梯。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/min-cost-climbing-stairs
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

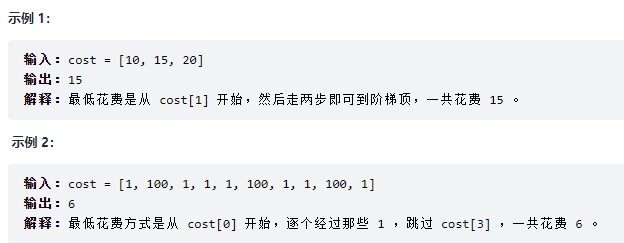
class Solution {
    public int minCostClimbingStairs(int[] cost) {

    }
}

 五部曲：确定数组、确定递推公式、dp数组初始化、确定遍历顺序、举例推导

方法：动态规划

最后返回倒数第一个和倒数第二个的最小值

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        if (cost == null || cost.length == 0) {
            return 0;
        }
        if (cost.length == 1) {
            return cost[0];
        }
        int[] dp = new int[cost.length];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for (int i = 2; i < cost.length; i++) {
            dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        //最后一步，如果是由倒数第二步爬，则最后一步的体力花费可以不用算
        return Math.min(dp[cost.length - 1], dp[cost.length - 2]);
    }
}

（二）路径数量

1、不同路径

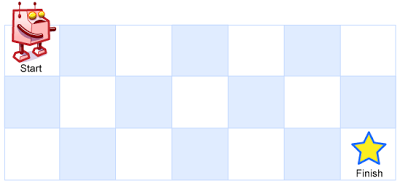
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/unique-paths
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 

 

class Solution {
    public int uniquePaths(int m, int n) {

    }
}

方法1：dfs深搜

class Solution {
private:
    int dfs(int i, int j, int m, int n) {
        if (i > m || j > n) return 0; // 越界了
        if (i == m && j == n) return 1; // 找到一种方法，相当于找到了叶子节点
        return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
    }
public:
    int uniquePaths(int m, int n) {
        return dfs(1, 1, m, n);
    }
};

方法2：动态规划

1. 确定dp数组的下标及含义：
   1. dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。
2. 确定递推公式
   1. dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
3. dp数组的初始化

   1. dp[i][0] = 1; dp[0][j] = 1;

4. 确定遍历顺序
   1. 从左到右
5. 举例推导

  /**
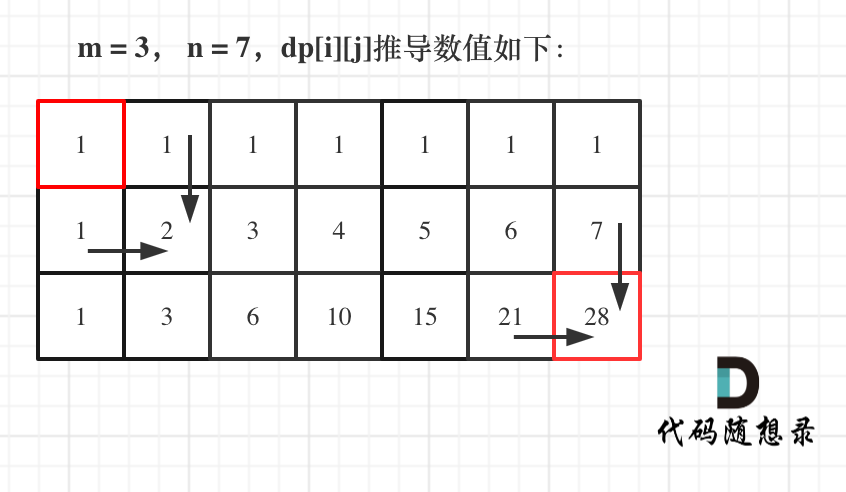
     * 1. 确定dp数组下表含义 dp[i][j] 到每一个坐标可能的路径种类
     * 2. 递推公式 dp[i][j] = dp[i-1][j] dp[i][j-1]
     * 3. 初始化 dp[i][0]=1 dp[0][i]=1 初始化横竖就可
     * 4. 遍历顺序 一行一行遍历
     * 5. 推导结果 。。。。。。。。
     *
     * @param m
     * @param n
     * @return
     */
    public static int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        //初始化
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }

2、不同路径 II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

 

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/unique-paths-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {

    }
}

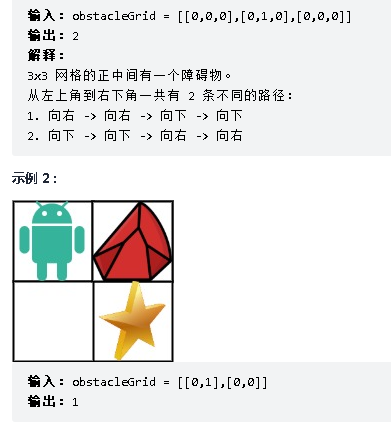
示例

 

 

 

 方法：动态规划

1. 确定dp数组的下标及含义：
   1. dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。
2. 确定递推公式

if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候，再推导dp[i][j]
    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}

　　3.dp数组的初始化

vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;

　　4.确定遍历顺序

　　　　从左到右一层一层遍历，这样保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。

　　5.举例推导

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int n = obstacleGrid.length, m = obstacleGrid[0].length;
        int[][] dp = new int[n][m];
        dp[0][0] = 1 - obstacleGrid[0][0];
        for (int i = 1; i < m; i++) {
            if (obstacleGrid[0][i] == 0 && dp[0][i - 1] == 1) {
                dp[0][i] = 1;
            }
        }
        for (int i = 1; i < n; i++) {
            if (obstacleGrid[i][0] == 0 && dp[i - 1][0] == 1) {
                dp[i][0] = 1;
            }
        }
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < m; j++) {
                if (obstacleGrid[i][j] == 1) continue;
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[n - 1][m - 1];
    }
}