算法--动态规划

一、概念

1、三要素
重叠（+备忘录）子问题、最优子结构、状态转移方程

2、（列状态转移方程）步骤

明确初始条件base case、明确状态、明确选择、定义dp数组/函数

 二、斐波那契数列

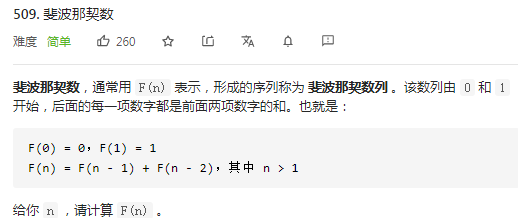
1、原始暴力递归

重复运算--重叠子问题

递归的时间复杂度

2、带备忘录的递归（自顶向下）

class Solution {
    //初始化备忘录为0
    int[] mome;
    public int fib(int n) {
        mome  = new int[n+1];
        if(n < 1) return 0;
        return comput(mome,n);
    }
    public int comput(int []mome,int n){
        if(n == 1 || n == 2) return 1;
        if(mome[n]!=0) return mome[n];
        mome[n] = comput(mome, n-1) + comput(mome, n-2);
        return mome[n];
    }
}

3、dp数组的迭代解法（自底向上）

class Solution {
    public int fib(int n) {
        if(n < 1) return 0;
        if(n == 1 || n ==2) return 1;
        int[] arr = new int[n+1]; //Java默认将数组初始化为0
        arr[1] = arr[2] = 1;
        for(int i = 3; i <= n; i++){
            arr[i] =arr[i-1] +arr[i-2];
        }
        return arr[n];
    }
}

4、状态压缩，空间复杂度变为O(1)

class Solution {
    public int fib(int n) {
        if(n < 1) return 0;
        if(n==1 || n==2) return 1;
        int prev=1,curr=1,sum;
        for(int i=3;i<=n;i++){
            sum = prev + curr;
            prev = curr;
            curr = sum;
        }
        return curr;
    }
}

三、凑零钱问题

 

 1、暴力递归

符合最优子结构，硬币不限数量。与真实考试拿第一不同

步骤：

明确初始条件base case（目标金额amount为0，硬币为0）、

明确状态（amount不断变小直到base case）、

明确选择（硬币面值）、

定义dp数组/函数（自顶向下的函数参数是状态变化量amount，返回值为要计算的量）

 

 

 

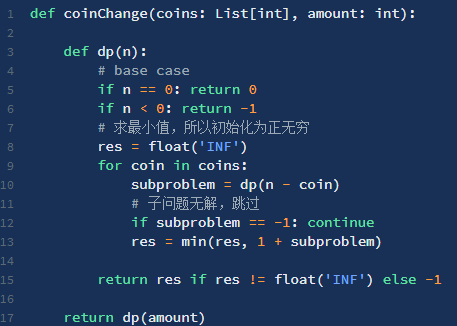
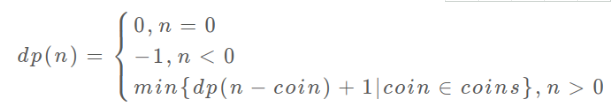
 2、带备忘录的递归

 3、dp数组的迭代解法（自底向上）

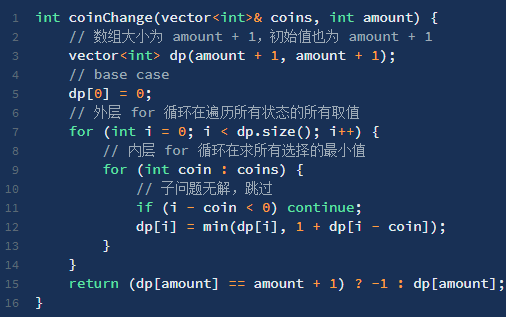
class Solution {
    public int coinChange(int[] coins, int amount) {
        if(amount < 0) return -1;
        int[] dp = new int[amount+1];
        Arrays.fill(dp,amount+1);
        dp[0] = 0;
        for(int i = 0; i < dp.length; i++){
            for(int coin:coins){
                if(i -coin < 0) continue;
                dp[i] = Math.min(dp[i],1+dp[i-coin]);
            }
        }
        return dp[amount]==amount+1?-1:dp[amount];
    }
}

此题不适合用Java语言dp函数自顶向下求

四、常见算法题

1、比特位计数

计算0到n中二进制下1的个数

 

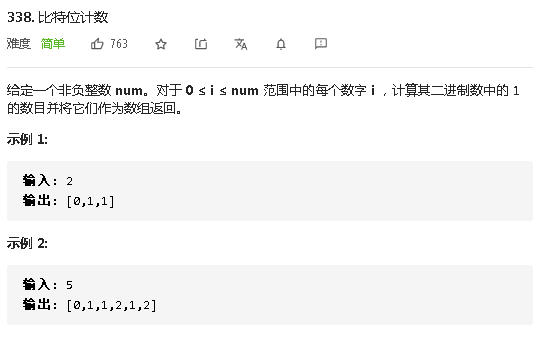
 方法一：动态规划

public int[] countBits(int num) {
    int dp[] = new int[num+1];
    for (int i = 0; i <= num/2; i++) {
        dp[i*2] = dp[i];
        if(i*2+1 <= num)
            dp[i*2+1] = dp[i] + 1;
    }
    return dp;
}

方法二：库函数

package com.iflytek;

import java.util.Arrays;

public class DP_bin_1 {
    public static void main(String[] args) {
        int[] count = testDp(5);
        //Arrays.asList(count).forEach(System.out::println); --只适用于对象类型的数组
        Arrays.stream(count).forEach(System.out::println);
    }
    public static int[] testIntegerBitCount(int n){

　　　　 int[] ans = new int[n+1];

        for (int i = 0; i <= n; i ++){

            ans[i] = Integer.bitCount(i);

        }

        return ans;

    }
    public static int[] testDp(int n){
        int[] dp = new int[n+1]; // java默认赋初值
        for (int i = 0; i < n/2; i++) {
            dp[2*i] = dp[i];
            if (2*i + 1 < n){
                dp[2*i+1] = dp[i] + 1;
            }
        }
        return dp;
    }
}

2、括号生成

生成匹配的括号组合