LeetCode 309. Best Time to Buy and Sell Stock with Cooldown

309. Best Time to Buy and Sell Stock with Cooldown

Add to List

Description Submission Solutions

• Total Accepted: 35948
• Total Submissions: 89944
• Difficulty: Medium
• Contributors: Admin

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:

• You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
• After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)

Example:

prices = [1, 2, 3, 0, 2]
maxProfit = 3
transactions = [buy, sell, cooldown, buy, sell]

Credits:
Special thanks to @dietpepsi for adding this problem and creating all test cases.

Subscribe to see which companies asked this question.

【题目分析】

相比之前的题目，这个有两个要求：在同一时间不能进行两次交易，在进行一次卖出操作以后必须暂停一天交易。

【思路】

动态规划的状态转移方程还是很难想出来的，很多状态转移还有空间优化的空间。这个题目不是很理解，下面列一下大家的解决方式。

1. 比较好理解的状态转移图

这道题可以用动态规划的思路解决。但是一开始想的时候总是抽象不出状态转移方程来，之后看到了一种用状态机的思路，觉得很清晰，特此拿来分享，先看如下状态转移图：

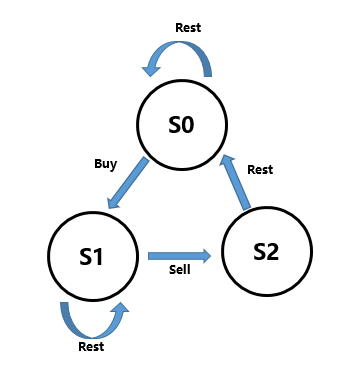
这里我们把状态分成了三个，根据每个状态的指向，我们可以得出下面的状态转移方程：

• s0[i] = max(s0[i-1], s2[i-1])
• s1[i] = max(s1[i-1], s0[i-1] - price[i])
• s2[i] = s1[i-1] + price[i]

这样就清晰了很多。

public class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        int[] s0 = new int[len];
        int[] s1 = new int[len];
        int[] s2 = new int[len];
        
        s1[0] = -prices[0];
        s0[0] = 0;
        s2[0] = Integer.MIN_VALUE;
        
        for (int i = 1; i < len; i++) {
            s0[i] = Math.max(s0[i - 1], s2[i - 1]);
            s1[i] = Math.max(s1[i - 1], s0[i - 1] - prices[i]);
            s2[i] = s1[i - 1] + prices[i];
        }
        return Math.max(s0[len - 1], s2[len - 1]);
    }
}

 

2. discuss里面的解法

The series of problems are typical dp. The key for dp is to find the variables to represent the states and deduce the transition function.

Of course one may come up with a O(1) space solution directly, but I think it is better to be generous when you think and be greedy when you implement.

The natural states for this problem is the 3 possible transactions : buy, sell, rest. Here rest means no transaction on that day (aka cooldown).

Then the transaction sequences can end with any of these three states.

For each of them we make an array, buy[n], sell[n] and rest[n].

buy[i] means before day i what is the maxProfit for any sequence end with buy.

sell[i] means before day i what is the maxProfit for any sequence end with sell.

rest[i] means before day i what is the maxProfit for any sequence end with rest.

Then we want to deduce the transition functions for buy sell and rest. By definition we have:

buy[i]  = max(rest[i-1]-price, buy[i-1]) 
sell[i] = max(buy[i-1]+price, sell[i-1])
rest[i] = max(sell[i-1], buy[i-1], rest[i-1])

Where price is the price of day i. All of these are very straightforward. They simply represents :

(1) We have to `rest` before we `buy` and 
(2) we have to `buy` before we `sell`

One tricky point is how do you make sure you sell before you buy, since from the equations it seems that [buy, rest, buy] is entirely possible.

Well, the answer lies within the fact that buy[i] <= rest[i] which means rest[i] = max(sell[i-1], rest[i-1]). That made sure [buy, rest, buy] is never occurred.

A further observation is that and rest[i] <= sell[i] is also true therefore

rest[i] = sell[i-1]

Substitute this in to buy[i] we now have 2 functions instead of 3:

buy[i] = max(sell[i-2]-price, buy[i-1])
sell[i] = max(buy[i-1]+price, sell[i-1])

This is better than 3, but

we can do even better

Since states of day i relies only on i-1 and i-2 we can reduce the O(n) space to O(1). And here we are at our final solution:

Java

public int maxProfit(int[] prices) {
    int sell = 0, prev_sell = 0, buy = Integer.MIN_VALUE, prev_buy;
    for (int price : prices) {
        prev_buy = buy;
        buy = Math.max(prev_sell - price, prev_buy);
        prev_sell = sell;
        sell = Math.max(prev_buy + price, prev_sell);
    }
    return sell;
}