LeetCode OJ 63. Unique Paths II

Follow up for "Unique Paths":

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

For example,

There is one obstacle in the middle of a 3x3 grid as illustrated below.

[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]

The total number of unique paths is 2.

Note: m and n will be at most 100.

---

【题目分析】

相比较上一个题目，在这个问题的grid中有部分区域是存在障碍物的，即有些区域不能到达。

---

【思路】

我们分析一下如果存在障碍物这个问题我们该如何解决。

1. 如果障碍物在入口或者出口，那么总的方法数就是0；

2. 如果障碍物在其他位置，那么存在障碍物的位置能到达的方法数为零；

在上一题中用到的方法在这个题目中也适用，只是需要判定一下当前是否是障碍物，如果是障碍物，则直接把能到达当前位置的方法数设置为0，否则：A[j] = A[j] +  A[j - 1]；

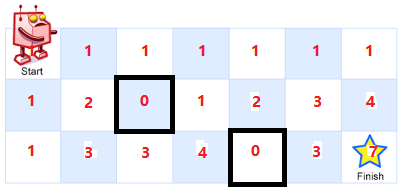
如上图中，黑框表示该位置存在障碍物，那么能到达这个位置的方法数只能被设置为0，然后按照动态规划的方法一行一行遍历，求出能到达每一个位置的方法数，直到求出能到达出口的方法数为止。

---

【java代码】

public class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int row = obstacleGrid.length;
        int col = obstacleGrid[0].length;
        
        if(row == 0 || col == 0) return 0;
        
        int[] dp = new int[col];
        dp[0] = 1;
        
        for (int i = 0; i < row; i++){
            if(obstacleGrid[i][0] == 1) dp[0] = 0;
            for (int j = 1; j < col; j++){
                if(obstacleGrid[i][j] == 1) dp[j] = 0;
                else dp[j] = dp[j - 1] + dp[j];
            }
        }
                
        return dp[col - 1];
    }
}