费舍尔精确检验

 

Fisher's 精确检验

用来检验一次随机实验的结果是否支持对于某个随机实验的假设。

a、随机事件发生的概率小于0.05则认定该事件为小概率事件。

b、一般原则认为在某个假设前提下，一次随机实验的结果不会出现小概率事件。

c、若一次随机实验的结果出现了小概率事件则认定该假设不被支持。

在给定假设（如零假设：事件间无显著相关性）的前提下，对假设事件的出现可能性做统计学检验，p-value越小，越能拒绝原假设。

p-value的含义：

 

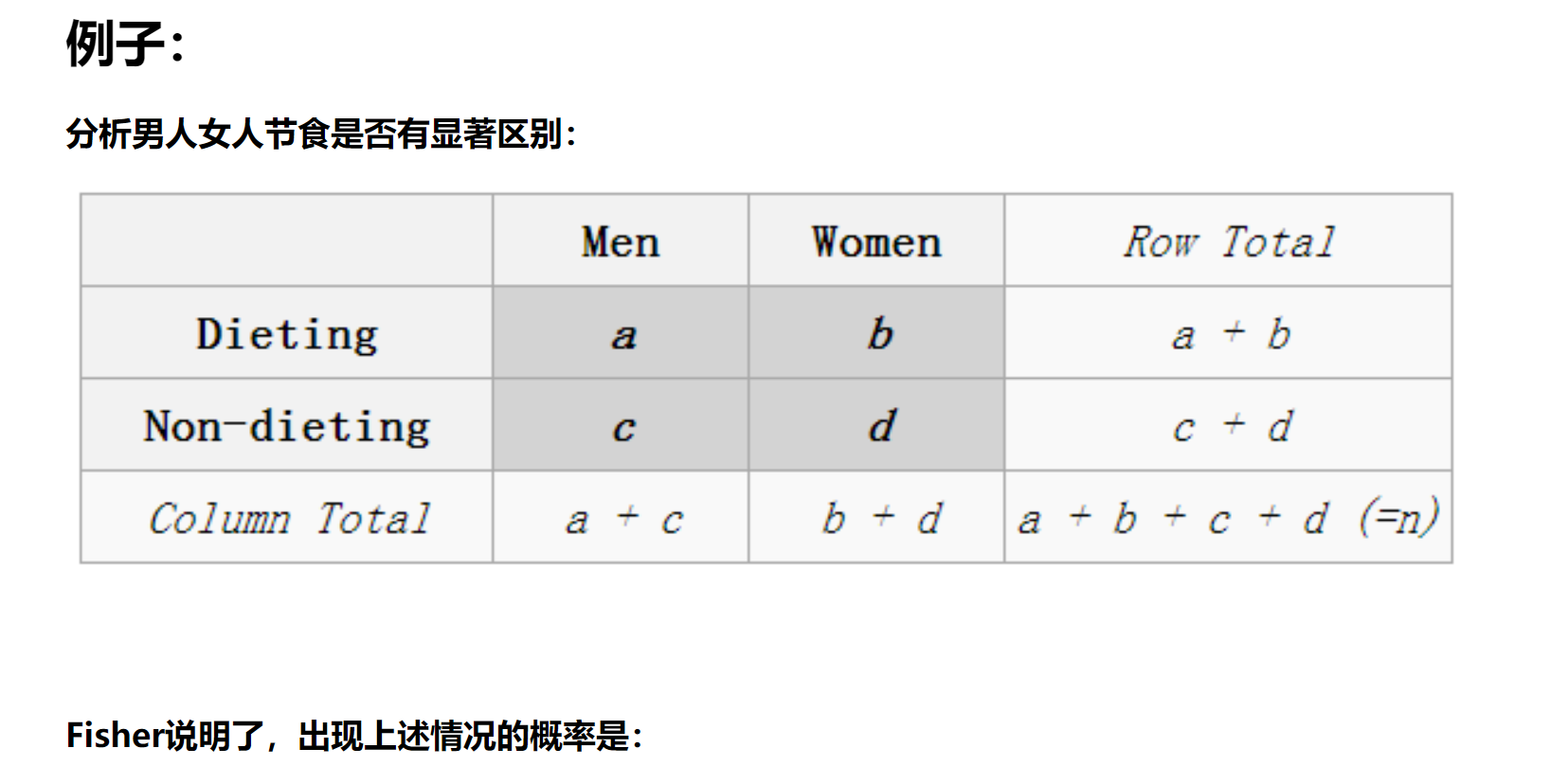
 P-value说明上述组合出现的概率。 

 

经典例子：吸烟与肺癌的产生有无关系的检测。

原假设：H0，吸烟与肺癌没有关系，P-value越小越能拒绝原假设。

 

001：如下的测试数据中，对吸烟和非吸烟的调查各100人（第二列和第三列）， 肺癌和非肺癌的个数在吸烟组和非吸烟组都是50，这说明

肺癌与吸烟没有任何关系，下面利用R语言统计检验，测试是否符合实际情况：

 

 

fisher.test(matrix(c(50,50,50,50),nrow=2))    ## 利用R语言的fisher.test进行测试

 

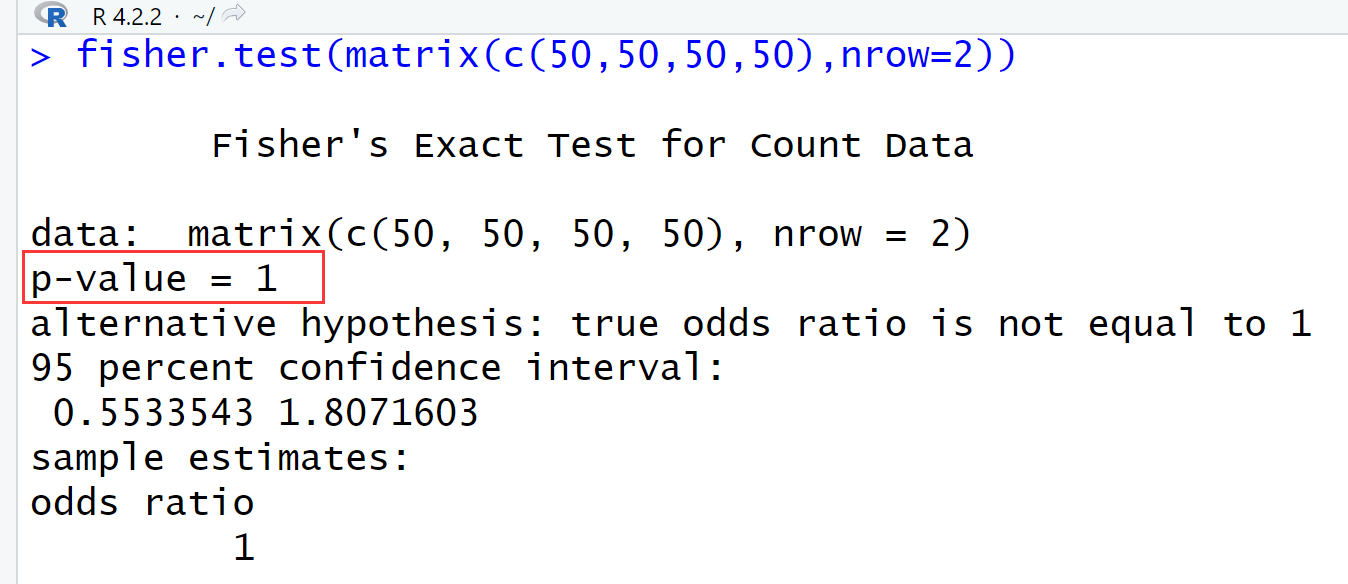
 可以看到P值为1（P值越小，越能拒绝原假设（原假设为吸烟和肺癌没有关系）），这里不能拒绝原假设，即原假设成立，吸烟和肺癌没有关系。

 

002、修改001中测试数据，并利用R语言重新测试，这里将测试数据修改为吸烟组肺癌人数为99，正常人数

为1；不吸烟组肺癌人数为2，正常人数为98，有此可以看出吸烟与肺癌有密切联系，可以预测P值将非常小，将拒绝原假设

 

 

fisher.test(matrix(c(99,1,2,98),nrow=2))    ## 费舍尔精确检验测试

 

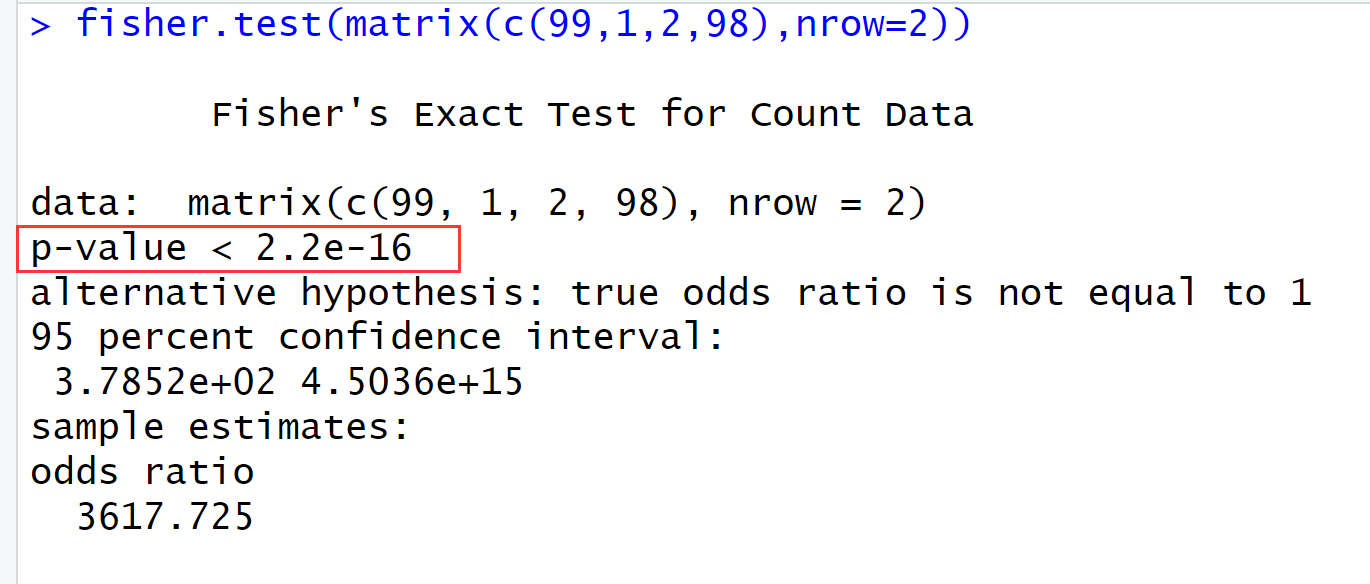
 可以看到p值非常的小，远远小于通常的0.05，所以这里拒绝原假设（吸烟和肺癌没有关系），得出结论吸烟和肺癌有密切关联。

 

003、修改测试数据，利用一组普通数据再次验证：

 

 

fisher.test(matrix(c(80,20,30,70),nrow=2))    ## 费舍尔精确检测测试

 

 

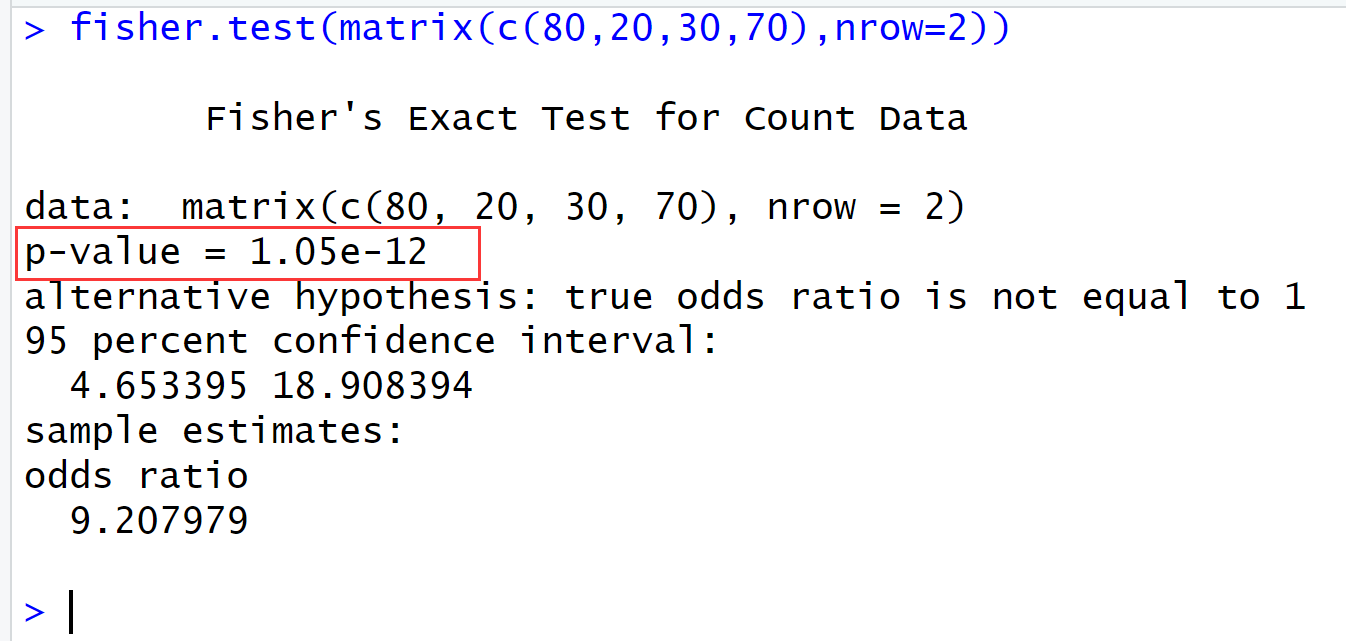
可以看到这里的p值e-12比上一个例子中的p值e-16增加了，这里主要是因为修改了测试数据，没有那么极端，但是这里p值任然较小，小于常规的阈值0.05，因此拒绝原假设，即吸烟和肺癌存在密切联系。

 

P值是如何计算的：

对于二维列联表，p值的计算如下：

 

 

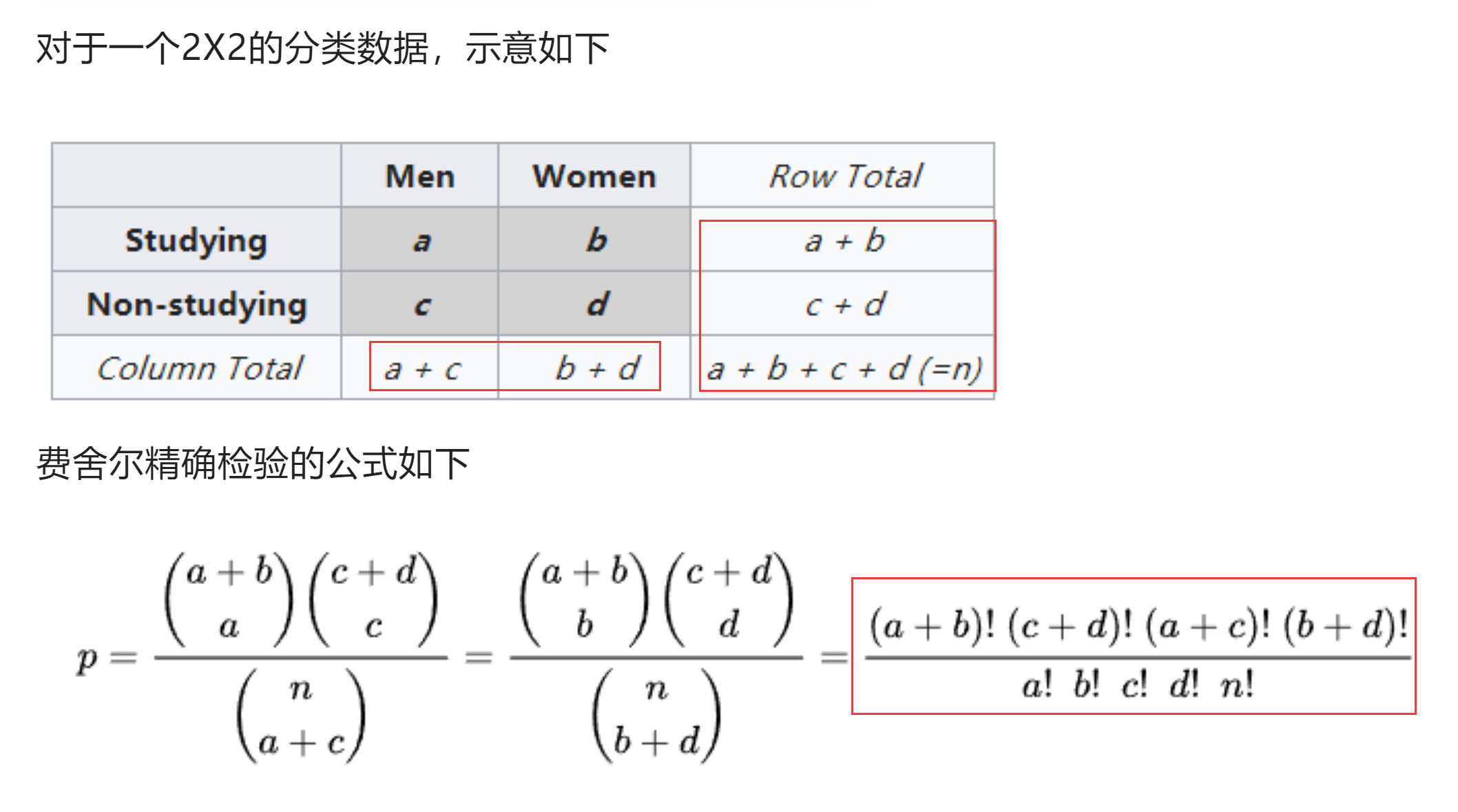
以如下测试数据进行验证：

 

 

p= （11！*  9！ * 10！ *  10！）/ (8! * 3! * 2! * 7! * 20!)

R语言中测试：

fisher.test(matrix(c(8, 2, 3, 7),nrow=2))    ## 费舍尔精确检验查看p值

factorial(11) * factorial(9) * factorial(10) * factorial(10)/(factorial(8) * 
              factorial(3) * factorial(2) * factorial(7) * factorial(20))   ## 手动计算p值

 

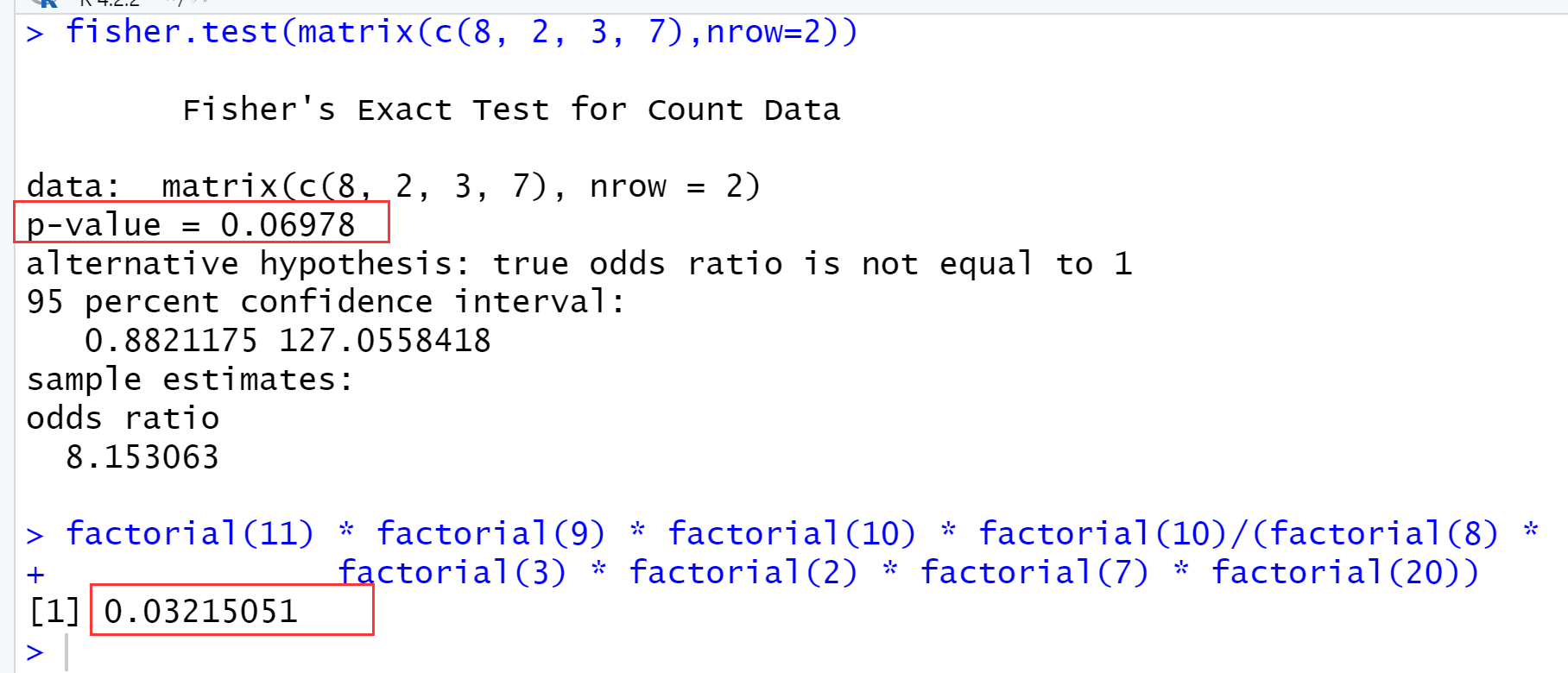
 P值貌似是两倍关系？？