R语言中矩阵的常规操作
001、
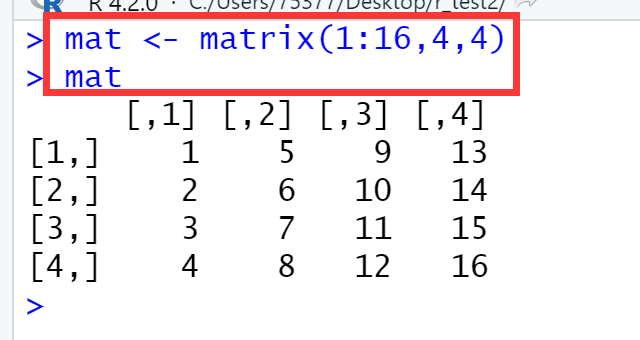
mat <- matrix(1:16, 4, 4) ## 生成矩阵 mat ## 显示矩阵
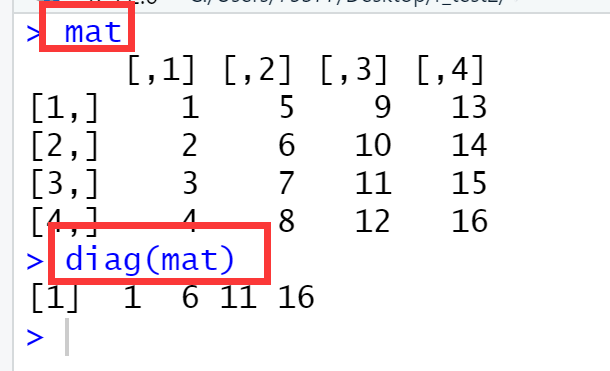
002、提取矩阵的对角线
mat
diag(mat) ## 提取矩阵的对角线
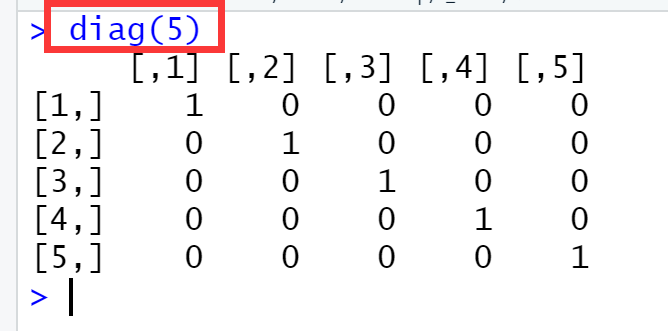
003、利用diag生成单位矩阵
diag(5) ## 生成单位矩阵
004、提取矩阵的上三角矩阵及下三角矩阵
mat
lower.tri(mat) ## 返回下三角矩阵的索引
mat[lower.tri(mat)] ## 提取下三角矩阵的元素
upper.tri(mat) ## 返回上三角矩阵的索引
mat[upper.tri(mat)] ## 提取上三角矩阵的元素

005、利用矩阵的下三角构建对称矩阵
mat mat1 <- mat mat1[upper.tri(mat1)] <- t(mat1)[upper.tri(mat1)] ## 以下三角矩阵构建对称矩阵 mat1
利用矩阵的上三角构建对称矩阵:
mat mat2 <- mat mat2[lower.tri(mat2)] <- t(mat2)[lower.tri(mat2)] ## 利用矩阵的上三角矩阵构建对称矩阵 mat2
006、将矩阵转换为行列的形式
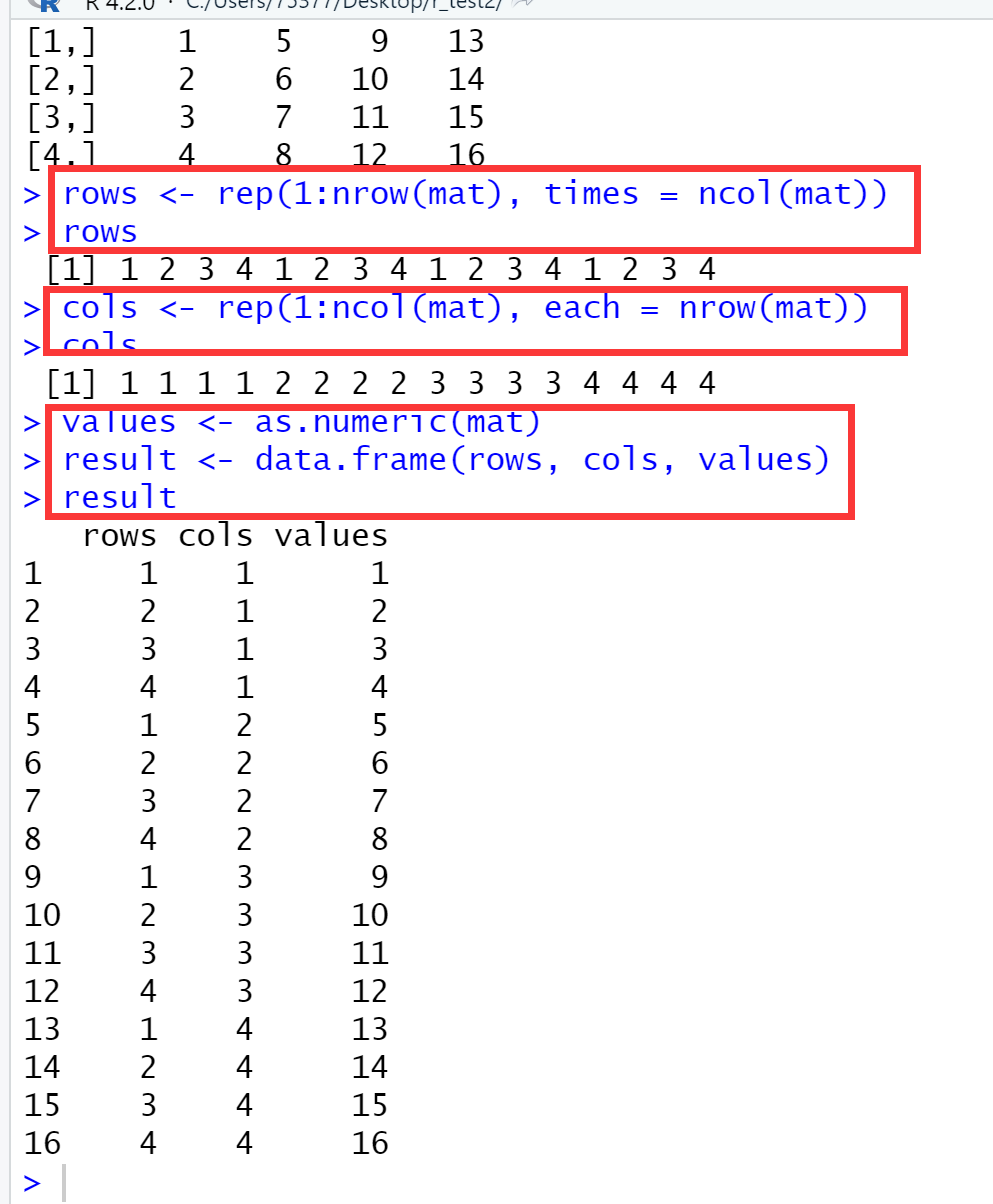
mat rows <- rep(1:nrow(mat), times = ncol(mat)) ## 生成行序号 rows cols <- rep(1:ncol(mat), each = nrow(mat)) ## 生成列序号 cols values <- as.numeric(mat) ## 返回矩阵的元素
result <- data.frame(rows, cols, values) ## 生成数据框
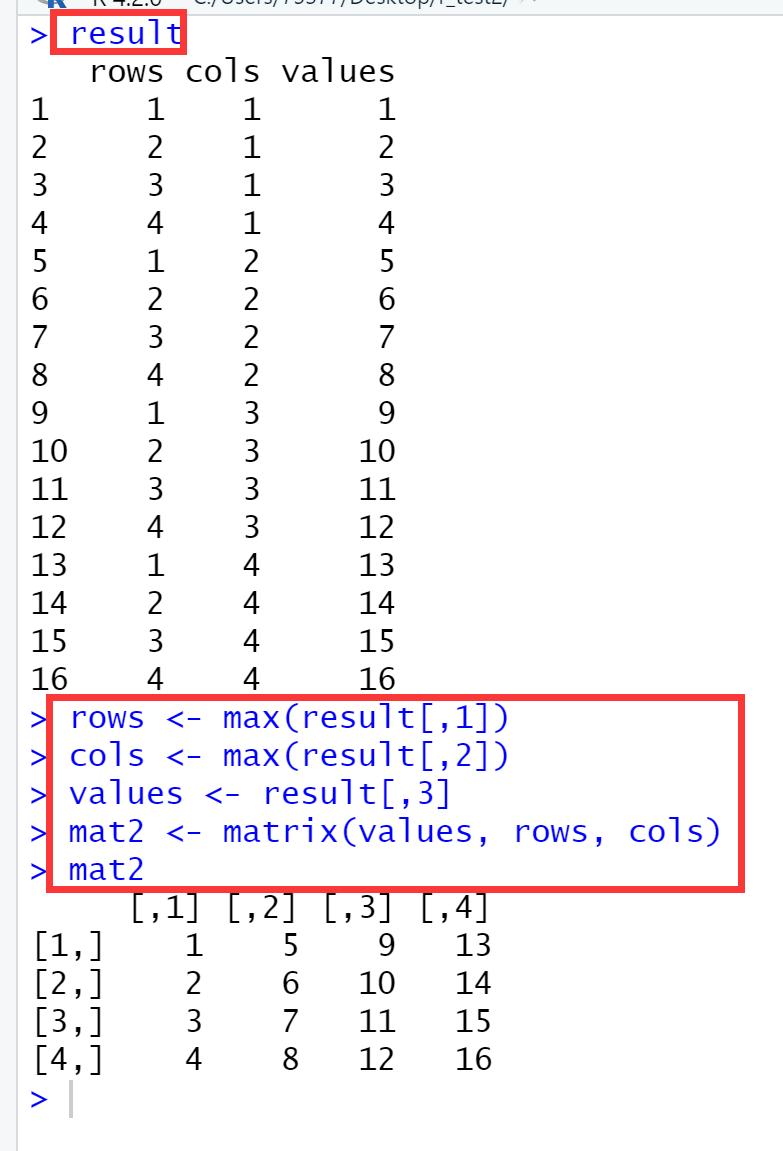
007、将三列的形式转换为矩阵
result rows <- max(result[,1]) ## 提取行数 cols <- max(result[,2]) ## 提取列数 values <- result[,3] ## 提取值 mat2 <- matrix(values, rows, cols) ## 生成矩阵 mat2
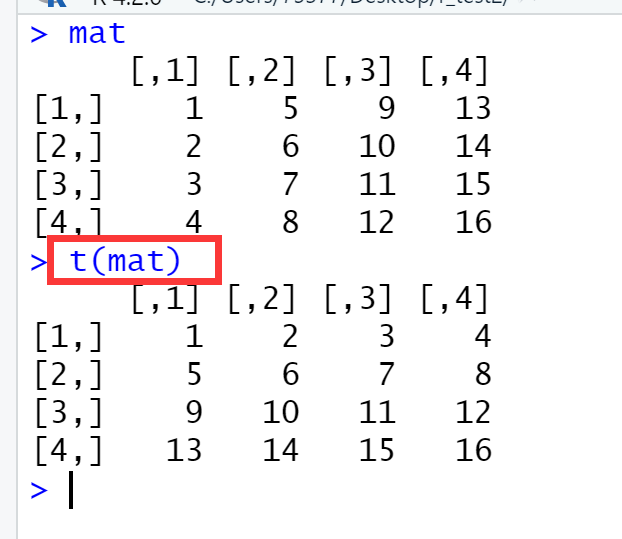
008、将矩阵转置
mat
t(mat) ## 将矩阵转置
009、矩阵相加减
mat1 <- matrix(1:16,4,4) mat2 <- mat1 ## 矩阵相加减仅适合同维度矩阵 mat1 mat2 mat1 + mat2 ## 矩阵相加 mat1 - mat2 ## 矩阵相减

010、数与矩阵相乘除
mat <- matrix(1:16,4,4) mat 2 * mat ## 数于矩阵相乘除 mat / 2

011、矩阵相乘(矩阵相乘的条件是左侧矩阵的列数等于右侧矩阵的行数, 矩阵相乘的结果的维度是左侧矩阵的行数,右侧矩阵的列数)
mat1 <- matrix(1:6, 2, 3) ## 两行三列的矩阵 mat1 mat2 <- matrix(1:6, 3, 2) ## 三行两列的矩阵 mat2 mat1 %*% mat2 ## 左侧矩阵的列数等于右侧矩阵的行数, 矩阵相乘的符号为%*%

012、计算t(A)%*%B的方法
方法1:
A <- matrix(1:12,3,4) B <- matrix(1:15,3,5) t(A) B t(A)%*%B ## 转置后矩阵相乘

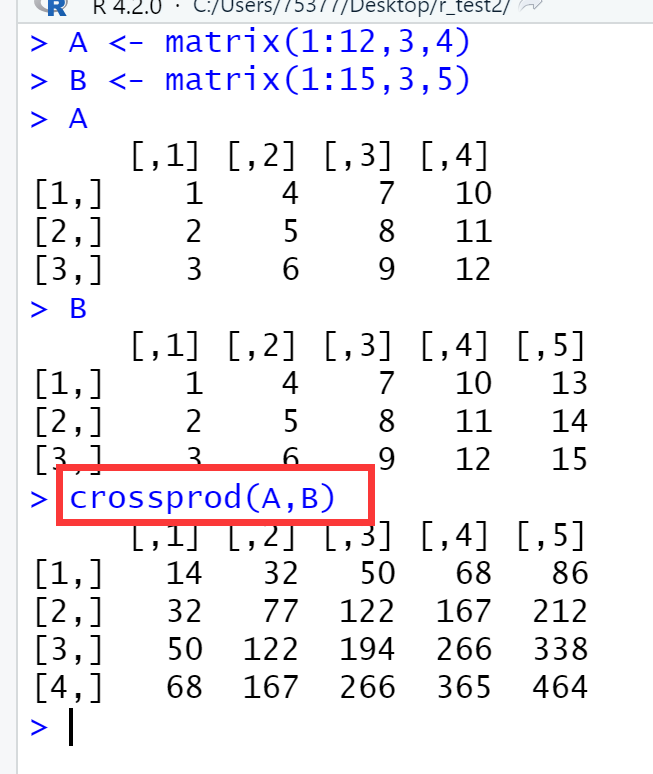
方法2:用crossprod函数,数据量大时效率更高
A <- matrix(1:12,3,4) B <- matrix(1:15,3,5) A B crossprod(A,B) ## 矩阵A转置后于矩阵B相乘





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律