42-MST&Prim&Kruskal

1. 最小生成树#

【加权图】一种为每条边关联一个权值的图模型；
【图的生成树】是该连通图的一个极小连通子图，含有图的全部顶点，但只有构成一棵树的(n-1)条边；
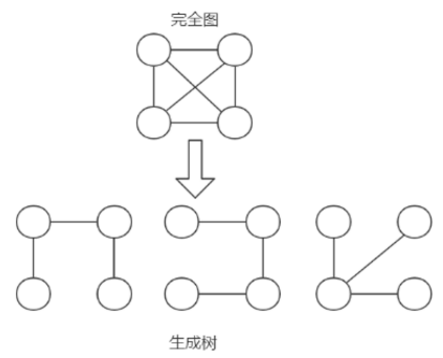
【加权图的最小生成树(MST)】在生成树的基础上，要求树的(n-1)条边的权值之和是最小的；

约定：

只考虑连通图
- 根据树的基本性质，我们要找的就是一个由V-1条边组成的集合，他们既连通了图中的所有顶点而权值之和又最小；
- 如果一幅图是非连通的，我们只能使用这个算法来计算它的所有连通分量的最小生成树，合并在一起称其为"最小生成森林"；
边的权重可能是 0 或者负数；所有边的权重都各不相同（如果可以相同，MST就不一定唯一了）。

计算 MST 的两种算法：

Prim 算法
Kruskal 算法

典型应用场景#修路问题：

2. Prim 算法#

2.1 思路分析#

从任意一个顶点开始，每次选择一个与当前顶点集最近的一个顶点，并将两顶点之间的边加入到顶点集中。然后继续找离更新后的这个顶点集最近的顶点 ....，就这么找下去，找够 n-1 条边；
{顶点集} 是逐渐增大的；
找 {当前最近顶点} 时使用到了贪婪算法；

设 G=(V,E) 是连通网，T=(U,D)是最小生成树，V,U是顶点集合，E,D是边的集合；
若从顶点u 开始构造最小生成树，则从集合V 中取出顶点u 放入集合U 中，标记顶点v 的 visited[u]=1；
若集合U 中顶点ui 与集合V-U 中的顶点vj 之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将顶点vj 加入集合U 中，将边(ui,vj) 加入集合D 中，标记 visited[vj]=1；
重复步骤②，直到 U 与 V 相等，即所有顶点都被标记为访问过，此时 D 中有 n-1 条边。

2.2 代码实现#

public class PrimDemo {
    public static void main(String[] args) {
        char[] datas = new char[] {'A','B','C','D','E','F','G'};
        int vertexs = datas.length;
        // 邻接矩阵 (∵ 是加权边 ∴ 表示两个顶点不连通得用个大数而非0)
        int[][] weightEdges = new int[][] {
            {10000,5,7,10000,10000,10000,2},
            {5,10000,10000,9,10000,10000,3},
            {7,10000,10000,10000,8,10000,10000},
            {10000,9,10000,10000,10000,4,10000},
            {10000,10000,8,10000,10000,5,4},
            {10000,10000,10000,4,5,10000,6},
            {2,3,10000,10000,4,6,10000}
        };
        
        MST mst = new MST();
        mst.createGraph(vertexs, datas, weightEdges);
        mst.showGraph();
        mst.prim(4);
    }
}

class MST {
    private Graph graph;
    
    public void createGraph(int vertexs, char[] datas, int[][] weightEdges) {
        graph = new Graph(vertexs);
        int i, j;
        for(i = 0; i < vertexs; i++) {
            graph.datas[i] = datas[i];
            for(j = 0; j < vertexs; j++)
                graph.weightEdges[i][j] = weightEdges[i][j];
        }
    }
    
    /**
     * 普利姆算法
     * @param v 从图的 v顶点 开始生成MST E.G. 'A' → 0, 'B' → 1 ...
     */
    public void prim(int v) {
        // 标记 顶点是否已被访问
        int[] visited = new int[graph.vertexs];
        // 把当前结点标记为 1
        visited[v] = 1;
        // 记录选定的2个顶点的索引
        int h1 = -1;
        int h2 = -1;
        
        int minWeight = 10000;
        // n个顶点, 找出 n-1 条边
        for(int k = 1; k < graph.vertexs; k++) {
            
            // 双重for: 确定 [新一次生成的子图(图越来越大)] 中, 哪两个顶点的权值最小
            // ~ 顶点i 表示被访问的结点(也同是子图中的顶点)
            for(int i = 0; i < graph.vertexs; i++) {
                // ~ 顶点j 表示还没有被访问的结点
                for(int j = 0; j < graph.vertexs; j++) {
                    // 子图越来越大, 需要if的次数也越来越多
                    if(visited[i] == 1 && visited[j] == 0 
                            && graph.weightEdges[i][j] < minWeight) {
                        minWeight = graph.weightEdges[i][j];
                        h1 = i;
                        h2 = j;
                    }
                }
            }
            System.out.printf("<%c, %c>\tweight = %d\n"
                    , graph.datas[h1], graph.datas[h2], minWeight);
            visited[h2] = 1;
            minWeight = 10000;
        }
    }
    
    public void showGraph() {
        graph.showGraph();
    }
}


class Graph {
    int vertexs; // 图中顶点个数
    char[] datas; // 顶点的值
    int[][] weightEdges; // 加权边
    
    public Graph(int vertexs) {
        this.vertexs = vertexs;
        datas = new char[vertexs];
        weightEdges = new int[vertexs][vertexs];
    }
    
    public void showGraph() {
        for(int[] link : weightEdges)
            System.out.println(Arrays.toString(link));
    }
}

3. Kruskal 算法#

Prim 算法是从 [顶点] 的角度来刻画生成树的，Kruskal 算法则是从 [边] 的角度来进行刻画的。

基本思想：按照权值从小到大的顺序选择 n-1 条边，并保证这 n-1 条边不构成回路。

具体做法：首先构造一个只含 n 个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止。

3.1 整个过程#

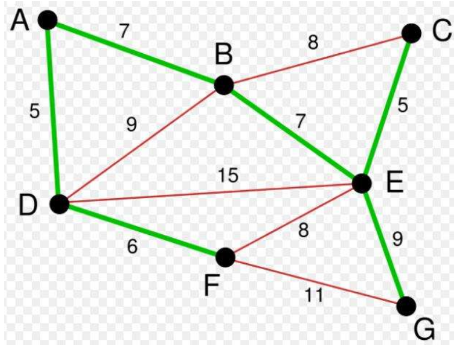
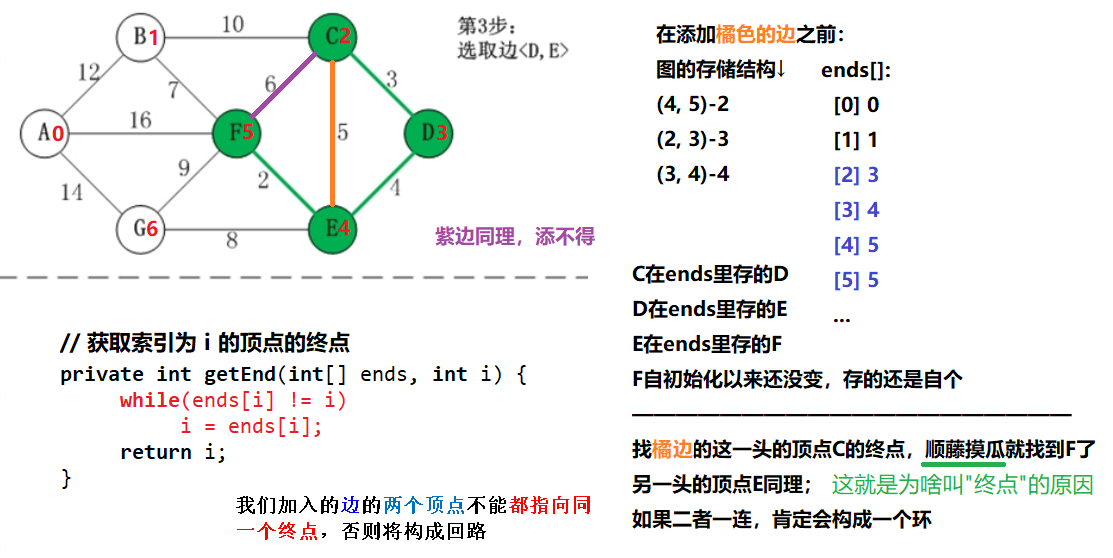
将边 <E,F> 加入 R 中：边 <E,F> 的权值最小，因此将它加入到最小生成树结果 R 中；
将边 <C,D>加入 R 中：上一步操作之后，边 <C,D> 的权值最小，因此将它加入到最小生成树结果 R 中；
将边 <D,E> 加入 R 中：上一步操作之后，边 <D,E> 的权值最小，因此将它加入到最小生成树结果 R 中；
将边 <B,F> 加入 R 中：上一步操作之后，边 <C,E> 的权值最小，但 <C,E> 会和已有的边构成回路；因此，跳过边 <C,E>。同理，跳过边 <C,F>。将边 <B,F> 加入到最小生成树结果 R 中；
将边 <E,G> 加入 R 中：上一步操作之后，边 <E,G> 的权值最小，因此将它加入到最小生成树结果 R 中；
将边 <A,B> 加入 R 中：上一步操作之后，边 <F,G> 的权值最小，但 <F,G> 会和已有的边构成回路；因此，跳过边 <F,G>。同理，跳过边 <B,C>。将边 <A,B> 加入到最小生成树结果 R 中；

此时，最小生成树构造完成！它包括的边依次是：<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。

3.2 延伸问题#

a. 按权值给边排序#

采用排序算法，我这里就无脑bubble了
还得给 '边' 整个数据结构(EdgeData)
- '边' 这头的顶点 - v1
- '边' 另一头的顶点 - v2
- '边' 的权值 - weight

b. 判断是否构成回路#

树的双亲表示法
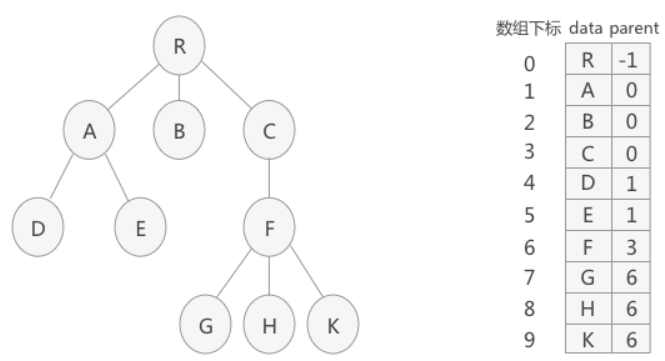
大概说下什么是 [并查集]
上面和判断构成回路有啥关系？
- 交并集是 一个用双亲表示法所表示的森林
- 可以利用这个结构来查找某一个顶点的双亲，进而找到根结点。这样，我们就能判断某两个顶点是否同源，在图中的表现就是加上这条边后会不会构成回路
- {并查集} 以顶点为基准，有几个顶点，就有几项
- 这里适用与顶点编号连续的情况；这样在 {并查集} 中，数组的下标就对应顶点的编号，数组的值就是这个顶点所在的双亲。这就是树的双亲表示法。高效率地利用数组下标
- 【BTW】下面提到的 "根" 和 "终点" 是一码事

3.3 算法步骤#

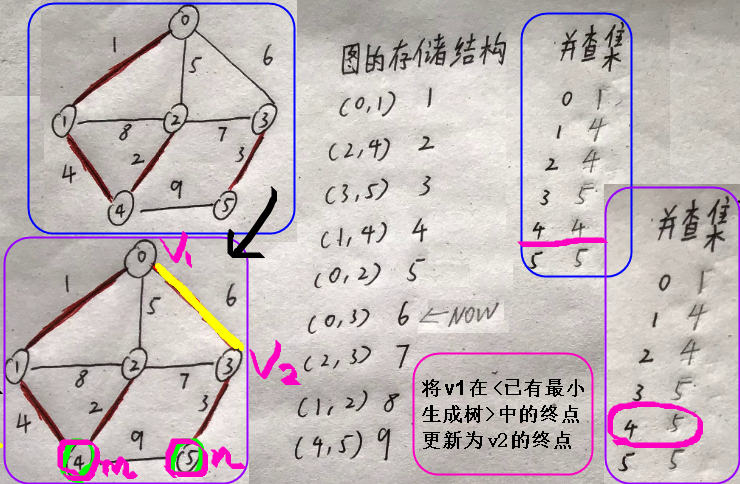
将边(EdgeData)构成的数组按照权值，从小到大排序；
对 { 并查集ends[] } 进行初始化，即把每一个位置中的值初始化为其对应下标；
选取 EdgeData[] 的第1项，查询该边所对应的顶点在 ends 中是否同源，同源则进行5，不同源则进行4；
若不同源，则把该边加入生成树，并修改 ends[v1的根] = v2的根；
若同源，则跳过，继续遍历EdgeData[]；
重复4~5，直到存储结构中所有的项被遍历；

3.4 代码实现#

public class KruskalCase {
    private int edgeNum;
    private char[] vertexs;
    private int[][] weightEdges;
    private EdgeData[] MST;
    // 使用 INF 表示 两个顶点不能连通
    private static final int INF = Integer.MAX_VALUE;
    
    public static void main(String[] args) {
        char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
        // 0 表示自连; * 表示连通; INF 表示不连通
        int weightEdges[][] = {
                        /*A*//*B*//*C*//*D*//*E*//*F*//*G*/
                /*A*/ {   0,  12, INF, INF, INF,  16,  14},
                /*B*/ {  12,   0,  10, INF, INF,   7, INF},
                /*C*/ { INF,  10,   0,   3,   5,   6, INF},
                /*D*/ { INF, INF,   3,   0,   4, INF, INF},
                /*E*/ { INF, INF,   5,   4,   0,   2,   8},
                /*F*/ {  16,   7,   6, INF,   2,   0,   9},
                /*G*/ {  14, INF, INF, INF,   8,   9,   0}
        }; 
        KruskalCase kc = new KruskalCase(vertexs, weightEdges);
        kc.printMatrix();
        kc.kruskal();
        kc.printMST();
    }

    // 构造器 (copy)
    public KruskalCase(char[] vertexs, int[][] weightEdges) {
        // 初始化 顶点
        int vLen = vertexs.length;
        this.vertexs = new char[vLen];
        // 初始化 MST
        MST = new EdgeData[vLen-1];
        for(int i = 0; i < vertexs.length; i++)
            this.vertexs[i] = vertexs[i];
        // 初始化 matrix
        this.weightEdges = new int[vLen][vLen];
        for(int i = 0; i < vLen; i++)
            for(int j = 0; j < vLen; j++)
                this.weightEdges[i][j] = weightEdges[i][j];
        // 统计 edge 数目
        for(int i = 0; i < vLen; i++)
            for(int j = i + 1; j < vLen; j++)
                if(weightEdges[i][j] != INF)
                    edgeNum ++;
    }
    
    public void kruskal() {
        // 表示最后结果数组的索引
        int index = 0; 
        // 用于保存 <已有~最小生成树> 中每个顶点在MST的双亲
        int[] ends = new int[edgeNum];
        for(int i = 0; i < ends.length; i++)
            ends[i] = i;
        // 获取 图 中所有的边的集合
        EdgeData[] edges = getEdges();
        sortEdges(edges);
        // 将 edge 添加到 MST
        for(int i = 0; i < edgeNum; i++) {
            // a. 获取 edge-i 的一头
            int v1 = getPosition(edges[i].start);
            // b. 获取 edge-i 的另一头
            int v2 = getPosition(edges[i].end);
            // c. 获取 v1 在 <已有~最小生成树> 中的终点
            int m = getEnd(ends, v1);
            // d. 获取 v2 在 <已有~最小生成树> 中的终点
            int n = getEnd(ends, v2);
            // e. 判断准备加入的 edge 是否构成 回路
            if(m != n) { // 不构成回路
                ends[m] = n; // 将 v1 在 <已有~最小生成树> 中的终点 更新为 v2 的终点
                MST[index++] = edges[i];
            }
            // 边数够了就没必要再继续下去了, 反正之后的边也肯定会构成回路
            if(index == MST.length) break;
        }
    }

    public void printMST() {
        System.out.println("最小生成树: ");
        for(int i = 0; i < MST.length; i++)
            System.out.println(MST[i]);
    }
    
    public void printMatrix() {
        System.out.println("matrix: ");
        for(int i = 0; i < vertexs.length; i++) {
            for(int j = 0; j < vertexs.length; j++)
                System.out.printf("%12d\t", weightEdges[i][j]);
            System.out.println();
        }
    }
    
    /**
     * 根据 顶点v的数据值 找到其对应的索引
     * @param v 顶点的数据值
     * @return 找不到返回 -1
     */
    private int getPosition(char v) {
        for(int i = 0; i < vertexs.length; i++)
            if(vertexs[i] == v)
                return i;
        return -1;
    }
    
    private void sortEdges(EdgeData[] edges) {
        EdgeData temp;
        for(int i = 0; i < edgeNum - 1; i++)
            for(int j = 0; j < edgeNum - 1 - i; j++)
                if(edges[j].weight > edges[j+1].weight) {
                    temp = edges[j];
                    edges[j] = edges[j+1];
                    edges[j+1] = temp;
                }
    }
    
    private EdgeData[] getEdges() {
        EdgeData[] edges = new EdgeData[edgeNum];
        int index = 0;
        for(int i = 0; i < vertexs.length; i++)
            // 关于主对角线对称
            for(int j = i + 1; j < vertexs.length; j++)
                if(weightEdges[i][j] != INF)
                    edges[index++] = new EdgeData(vertexs[i], vertexs[j], weightEdges[i][j]);
        return edges;
    }
    
    /**
     * 获取索引为 i 的顶点的终点(是终点!!!不是双亲!!!)
     * @param i
     * @param ends 记录了各个顶点对应的双亲!(该数组是逐步形成的)
     * @return 索引为i的顶点 对应的 终点的索引
     */
    private int getEnd(int[] ends, int i) {
        // 如果ends[v] = v, 则它就是根; 否则就让v = ends[v], 向上寻找, 直到其相等
        while(ends[i] != i)
            i = ends[i];
        return i;
    }
    
}

class EdgeData {
    // 边的两头上的点
    char start;
    char end;
    // 边的权重
    int weight;
    
    public EdgeData(char start, char end, int weight) {
        super();
        this.start = start;
        this.end = end;
        this.weight = weight;
    }

    @Override
    public String toString() {
        return "[" + start + ", " + weight + ", " + end + "]";
    }
}