38-动态规划
1. 算法介绍
- 动态规划(Dynamic Programming)算法的核心思想是：将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法；
- 动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解；
- 与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）；
- 动态规划可以通过填表的方式来逐步推进，得到最优解。
DP is just a kind of smart recursion
2. 理论知识
摘自：http://www.imooc.com/article/283103
2.1 最优化原理
最优化原理指的最优策略具有这样的性质：
不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简单来说就是一个最优策略的子策略也是必须是最优的，而所有子问题的局部最优解将导致整个问题的全局最优。如果一个问题能满足最优化原理，就称其具有最优子结构性质。
这是判断问题能否使用动态规划解决的先决条件，如果一个问题不能满足最优化原理，那么这个问题就不适合用动态规划来求解。
这样说可能比较模糊，来举个栗子吧。
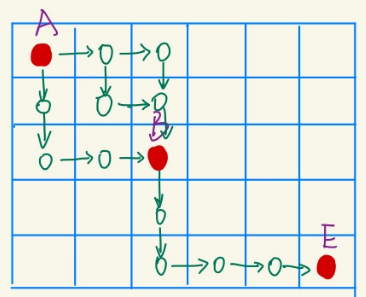
如下图，求从A点到E点的最短距离，那么子问题就是求从A点到E点之间的中间点到E点的最短距离，比如这里的B点。那么这个问题里，怎么证明最优化原理呢？
我们假设从A点到E点的最短距离为d，其最优策略的子策略假设经过B点，记该策略中B点到E点的距离为d1，A点到B点的距离为d2；
我们可以使用反证法，假设存在B点到E点的最短距离d3，并且d3 < d1，那么 d3 + d2 < d1 + d2 = d，这与d是最短距离相矛盾；所以，d1是B点到E点的最短距离；
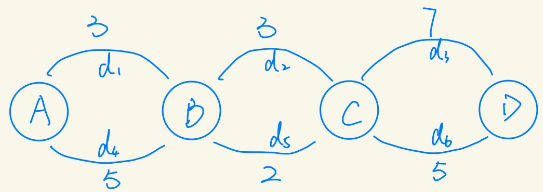
为了增加理解，这里再举一个反例；图中有四个点，A、B、C、D，相邻两点有两条连线，代表两条通道，d1, d2, d3, d4, d5, d6 代表的是道路的长度，求A到D的所有通道中，总长度除以4得到的余数最小的路径为最优路径，求一条最优路径。
这里如果还是按照上面的思路去求解，就会误入歧途了！按照之前的思路，A的最优取值应该可以由B的最优取值来确定，而B的最优取值为（3+5）mod 4 = 0；所以应该选d2和d6这两条道路。而实际上，全局最优解是d4+d5+d6或者d1+d5+d3；所以这里子问题的最优解并不是原问题的最优解，即不满足最优化原理。所以就不适合使用动态规划来求解了。
2.2 无后效性
无后效性指的是某状态下决策的收益，只与状态和决策相关，与到达该状态的方式无关。某个阶段的状态一旦确定，则此后过程的演变不再受此前各种状态及决策的影响。
换句话说，未来与过去无关，当前状态是此前历史状态的完整总结，此前历史决策只能通过影响当前的状态来影响未来的演变。再换句话说，过去做的选择不会影响现在能做的最优选择，现在能做的最优选择只与当前的状态有关，与经过如何复杂的决策到达该状态的方式无关。
这也是用来验证问题是否可以使用动态规划来解答的重要方法。
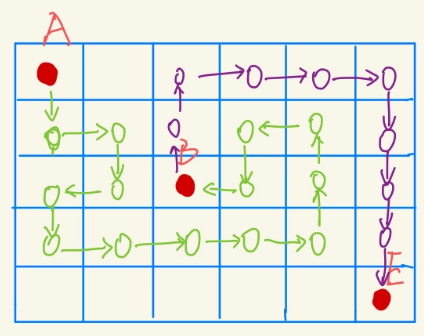
再回头看看上面的最短路径问题，如果在原来的基础上加上一个限制条件：同一个格子只能通过一次。
- 那么， 这个题就不符合无后效性了，因为前一个子问题的解会对后面子问题的选择策略有影响；
- 比如说，如果从A到B选择了一条如下图中绿色表示的路线，那么从B点出发到达E点的路线就只有一条了；也就是说从A点到B点的路径选择会影响B点到E点的路径选择。
3. 01背包问题
指一个给定容量的背包、若干具有一定价值和重量的物品，如何选择物品放入背包使物品的价值最大。其中又分 [01背包：每个物品最多放一个] 和 [完全背包：每种物品都有无限件可用]。
背包问题，需使用动态规划，即分解子问题，通过局部最大值，逐渐得到全局最大值。
3.1 伪码思路
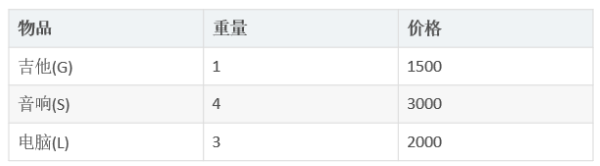
- 【变量】即对于给定的 n 个物品，设v[i]、w[i]分别为第 i 个物品的 价值(value) 和 重量(weight)
- C 为背包的容量
- v[i][j] 表示在 {前 i 个物品} 中能够装入 {容量为 j 的背包} 中的 最大价值
- 【限定条件】X1 * w[1] + X2 * w[2] + X3 * w[3] + … + Xn * w[n] ≤ C // Xi 表示第 i 个物品的数量
- 【图解】分解子问题，通过局部最大值逐渐得到全局最大，需要用到表格的分析
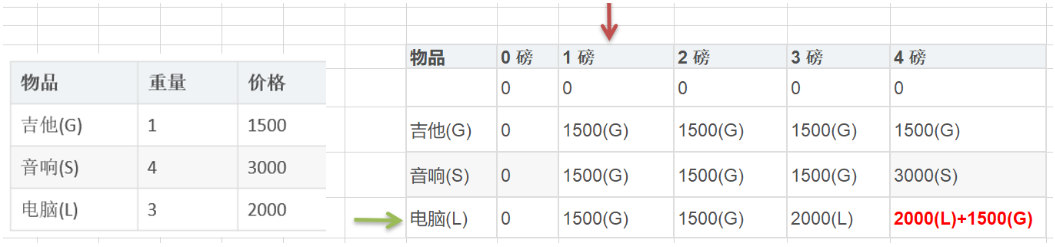
每次遍历到的第 i 个物品，根据 w[i] 和 v[i] 来确定是否需要将该物品放入背包中，则我们有下面的结果：
- v[i][0] = v[0][j] = 0
- 表第一行和第一列填入0
- 第一行全0：如果没有物品(i = 0)可供装载，不管背包容量C 有多大，背包的价值都是0
- 第一列全0：如果背包容量C = 0，同理
- 判断 {商品i 的重量} 与 {背包容量C} 的关系
- 当 w[i] > j 时，v[i][j] = v[i - 1][j]
- {准备加入的新增商品的容量} > {当前背包的容量} 时
- 就直接使用上一个单元格的装入策略，即 对于同等背包容量C，在有这个新增商品之前，背包是怎么装的，这里就怎么装
- 当 w[i] <= j 时，v[i][j] = max { v[i - 1][j]，value[i] + v[i-1][j - w[i]] }
- {准备加入的新增商品的容量} <=
- v[i-1][j]：上一个单元格的装入策略
- value[i]：当前商品的价值
- v[i-1][j-w[i]]：装入 {i-1商品}，到 {剩余空间 j-w[i]} 的最大值
- 当 w[i] > j 时，v[i][j] = v[i - 1][j]
3.2 代码实现
public class KnapsackProblem {
public static void main(String[] args) {
int[] weight = {1, 4, 3}; // 物品的重量
int[] value = {1500, 3000, 2000}; // 物品的价值
int c = 4; // 背包的容量
knapsack(weight, value, c);
}
public static void knapsack(int[] weight, int[] value, int c) {
// 创建二维数组(全0行 & 全0列)
// v[i][j]: 在 {前 i 个物品} 中能够装入 {容量为 j 的背包} 中的 最大价值
int[][] v = new int[value.length+1][c+1];
int[][] path = new int[value.length+1][c+1];
// 1. 初始化第1行和第1列
for(int i = 0; i < v.length; i++)
v[i][0] = 0;
for(int j = 0; j < v[0].length; j++)
v[0][j] = 0;
// 根据公式动态规划处理
for(int i = 1; i < v.length; i++) { // 不处理 L1
for(int j = 1; j < v[i].length; j++) { // 不处理 C1
// 判断 {商品i的重量}与{背包容量C} 的关系 (i从1开始, 但第1个物品索引是0)
if(weight[i-1] > j) {
v[i][j] = v[i-1][j];
} else {
// v[i][j] = Math.max(v[i-1][j], value[i-1] + v[i-1][j-weight[i-1]]);
// 为了记录 物品存放背包的情况, 不能使用公式
int a = v[i-1][j], b = value[i-1] + v[i-1][j-weight[i-1]];
if(a < b) { // 最优情况, 才记录path
v[i][j] = b;
path[i][j] = 1;
} else {
v[i][j] = a;
}
}
}
}
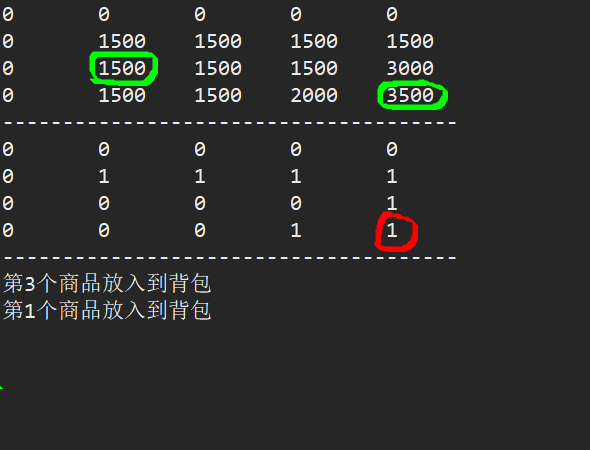
// 输出 v
for(int i = 0; i < v.length; i++) {
for(int j = 0; j < v[i].length; j++)
System.out.print(v[i][j] + "\t");
System.out.println();
}
System.out.println("--------------------------------------");
// 输出 path
for(int i = 0; i < path.length; i++) {
for(int j = 0; j < path[i].length; j++)
System.out.print(path[i][j] + "\t");
System.out.println();
}
System.out.println("--------------------------------------");
// 输出背包的放置情况
int i = path.length - 1; // 最大行索引
int j = path[0].length - 1; // 最大列索引
while(i > 0 && j > 0) { // 反向查找!
if(path[i][j] == 1) {
System.out.printf("第%d个商品放入到背包\n", i);
j -= weight[i-1];
}
i--;
}
}
}
