Tukey‘s test方法 异常值

如何计算异常值

异常值就是和其他样本数据有显著差异的值。这个词在统计学中经常用到，可以表示数据异常或测量错误。明白算异常值的方法，对于正确理解数据非常有用，而且会引出更精确的结论。以下介绍一个很简单的算异常值的过程和方法。

 

 

# 引用numpy模块
import numpy as np

#求数组a的中位数
np.median(a)

#求数组a的四分位数
np.percentile(a, [25, 50, 75])

　

 

　

 

 

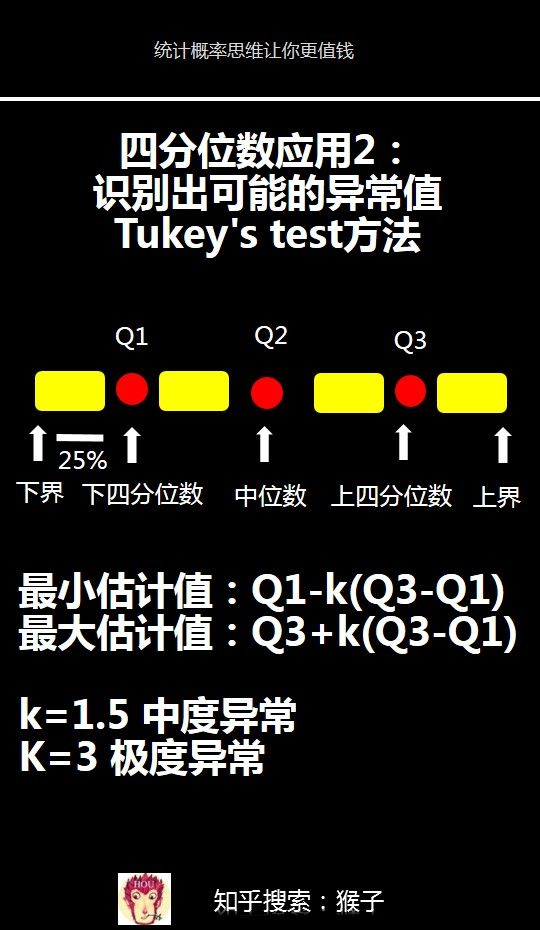
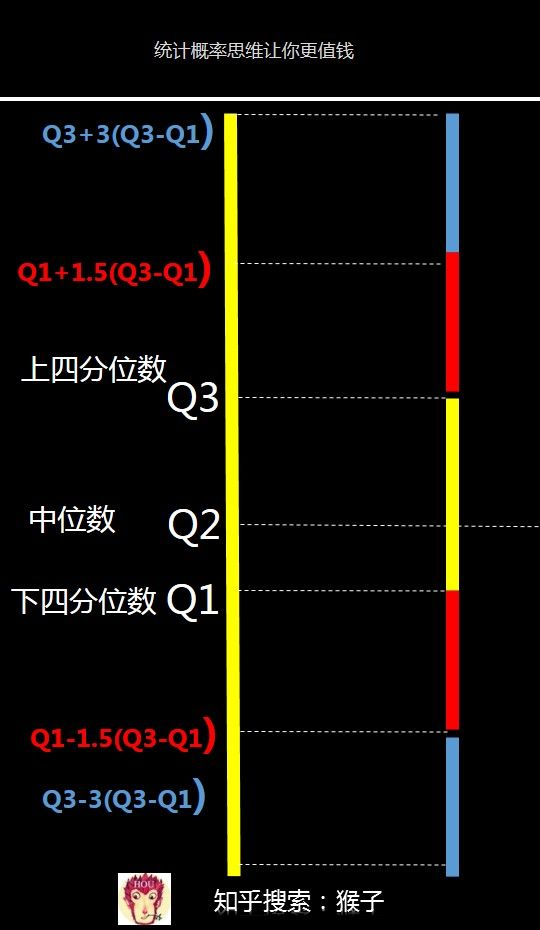
步骤

1. 
    
   了解如何认出潜在异常值。计算之前先辨认数据中的潜在异常值。比如一列数据，表示的是房间内12个东西的温度。如果其中11个的温度在70华氏度（21摄氏度左右）内，第12个却跑到300华氏度（约150摄氏度）了，那你可以粗略判断这是一个异常值。
    
2. 
    
   把数据从小到大排列。以以上数据为例，继续考虑房间内物体温度： {71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}，变更顺序为: {69, 69, 70, 70, 70, 70, 71, 71, 71, 72, 73, 300}.
    
3. 
    
   计算中位数。中位数是一串数据中间的一个数据点，如果数据总数是偶数，那么中间两位数的平均数就是中位数。上面数据中，中间两项是70、71，则中位数是((70 + 71) / 2)或70.5
    
4. 
    
   计算下四分位数，这里设置为Q1，表示总数据最小的25%的数据在这个点以下。在上面例子中，又有两个数据要被平分，即((70 + 70) / 2) 或 70
    
5. 
    
   计算上四分位数，设置为Q3，表示最大的25%数据都在这个点以上。本例子中Q3 是71、72的平均数，即 71.5
    
6. 
    
   找出数据的“内围”。第一步是把Q1和Q3的差（四分位差）乘以1.5。上面的例子中，四分位差是(71.5 - 70)得 1.5。再乘以1.5 得 2.25 ，加上Q3 ，用Q1 减去这个和，得到内围。本例中内围是67.75 and 73.75.

   • 任何在这个范围外的数字都是“平稳界外值”。本例子中，只有300华氏度是在范围以外的，即是所谓的平稳界外值。
    
7. 
    
   找出数据外围。和内围方法类似，不过这里要将四分位差乘以3 而非1.5。乘以3即(1.5 * 3) 得到 4.5。得到外围是65.5 、 76

   • 任何这个范围以外的数字，都算是“极端界外值”，300度也在这个范围外，因此也算“极端界外值”