Python实现冒泡、选择、插入、快排、堆排、归并排序
1 算法
正如阿基米德用浮力知识帮助国王判断出来工匠有没有掺假一样,算法就是在有限的时间里一步步执行某些任务的过程,
判断一个算法的好坏,时间和空间复杂度是两个非常重要的指标,相对来说,时间复杂度更为重要,对于公司来讲,迫不
得已的时候需要空间换时间,牺牲物理空间来换取用户的良好体验。
1 首先简单了解一下一个算法的时间复杂度


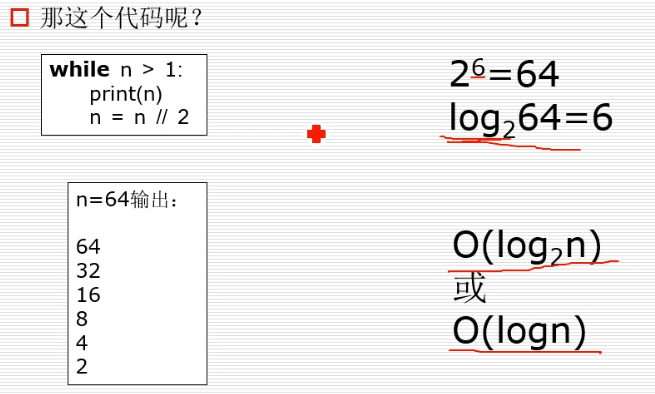

2 递归算法的简单应用
汉诺塔是源于印度一个古老传说,益智上帝创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上安大小顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘,说重新摆好之时就是世界毁灭之时,请问如果一秒摆一次,多久后世界会毁灭?
# recurision.py使用递归解决汉诺塔游戏问题 def hanoi(n,A,B,C): if n > 0: hanoi(n-1,A,C,B) print("%s->%s" % (A, C)) hanoi(n-1,B,A,C) hanoi(3,"A","B","C")
# 将3改为64就是题中答案,使用了递归的思想,发现那是几千亿年以后以后的事儿了
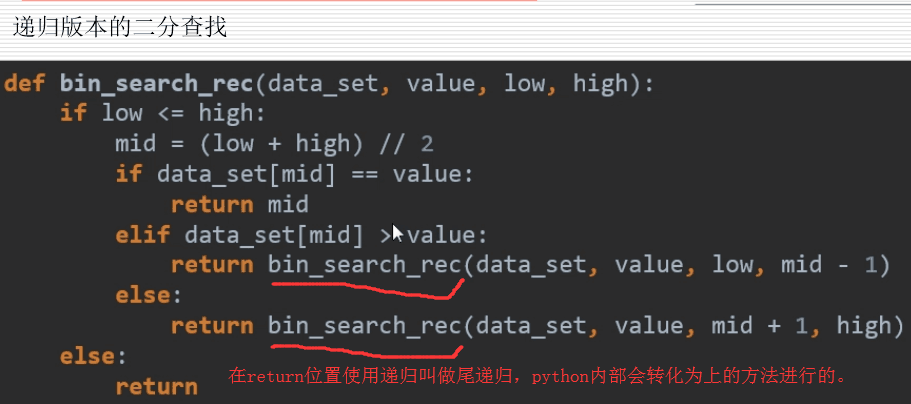
3 二分查找

# cal_time是一个计算时间的装饰器,下面的算法都能用的上 import time def cal_time(func): def wrapper(*args, **kwargs): t1 = time.time() result = func(*args, **kwargs) t2 = time.time() print("%s running time: %s secs." % (func.__name__, t2-t1)) return result return wrapper
# binary_search.py是二分查找,这里直接用的while循环解决的问题,
# 没有使用递归的思想,下面给出了递归版的二分查找,其实如果像这种尾
# 递归的话,Python内部会自动转化为while循环来进行
from suanfa.cal_time import cal_time # 二分查找代码 @cal_time def binary_search(li, val): low = 0 high = len(li) - 1 while low <= high: mid = (low + high) // 2 if li[mid] > val: high = mid - 1 elif li[mid] < val: low = mid + 1 else: return mid else: return None # Python列表的index方法 @cal_time def linear_search(li, val): try: i = li.index(val) return i except: return None # 随便找个列表对比上面两种方法查找速度 li = list(range(0,1000000)) print(binary_search(li,300000)) print(linear_search(li,300000))
冒泡

# bubble_sort.py是冒泡排序 from suanfa.cal_time import cal_time # 正常的冒泡排序 @cal_time def bubble_sort(li): for i in range(0, len(li)-1): # i表示第i趟 有序区有i个数 for j in range(0, len(li)-i-1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1],li[j] # 如果冒泡排序中执行一趟而没有交换,则列表已经是有序状态,可以直接结束算法 # 优化后的为: @cal_time def bubble_sort_2(li): for i in range(0, len(li)-1): # i表示第i趟 有序区有i个数 exchange = False for j in range(0, len(li)-i-1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1],li[j] exchange = True if not exchange: return import random li = list(range(1000)) random.shuffle(li) # bubble_sort(li) bubble_sort_2(li) print(li)
选择

# select_sort选择排序 from suanfa.cal_time import cal_time @cal_time def select_sort(li): for i in range(len(li)-1): # 第i趟:有序区li[0:i] 无序区li[i:n] min_loc = i for j in range(i+1,len(li)): if li[min_loc] > li[j]: min_loc = j li[min_loc], li[i] = li[i], li[min_loc] import random li = list(range(1000)) random.shuffle(li) select_sort(li) print(li)
插入
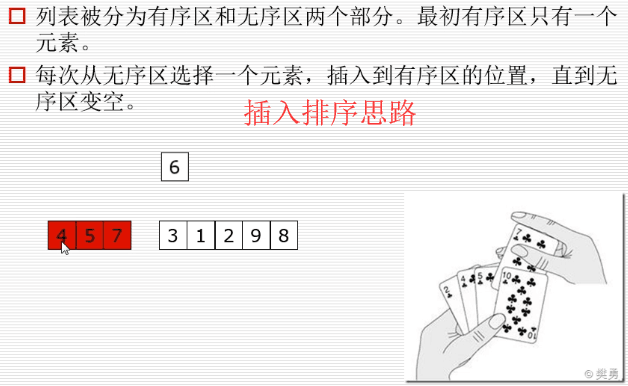
# insert_sort插入排序 from suanfa.cal_time import cal_time @cal_time def insert_sort(li): for i in range(1, len(li)): # i既表示趟数,也表示摸到的牌的下标 j = i - 1 tmp = li[i] while j >= 0 and li[j] > tmp: li[j+1] = li[j] j -=1 li[j+1] = tmp import random li = list(range(1000)) random.shuffle(li) insert_sort(li) print(li)
快排
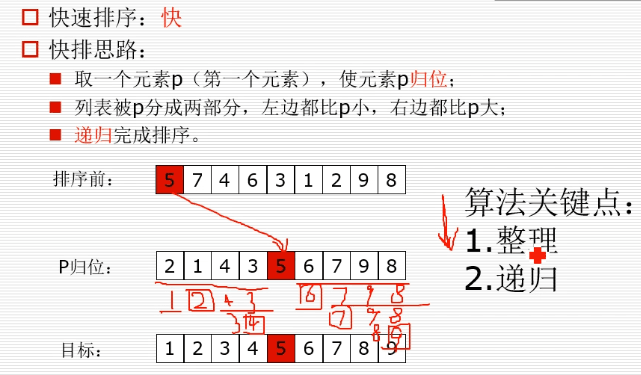
# quick_sort快速排序 from suanfa.cal_time import cal_time # 使用递归 def _quick_sort(li,left,right): if left < right: mid = partition(li, left, right) _quick_sort(li, left, mid-1) _quick_sort(li, mid+1, right) # 上面是递归函数,不能直接使用装饰器,不然会打印很多此时间,这里将上面的 # 递归函数装一个壳子,这个壳子不是递归函数,可以直接使用装饰器 @cal_time def quick_sort(li): return _quick_sort(li, 0, len(li)-1) # 使用最左边的这个数(赋值给tmp)进行归位的方法:从最右边网左边找小于这个数的数, # 并放在这个数的位置上面,再从最左边往右找大于这个数的数,放在最右边刚才移走的那 # 个数的位置上 def partition(li,left, right): tmp = li[left] while left < right: # 从右边找比tmp小的数 while left < right and li[right] >=tmp: right -= 1 li[left] = li[right] # 从左边找比tmp大的数 while left < right and li[left] <= tmp: left += 1 li[right] = li[left] li[left] = tmp return left # 上面是快排方法,下面用系统的排序方法对比一下速度 @cal_time def sys_sort(li): li.sort() import random li = list(range(1000)) random.shuffle(li) # quick_sort(li) sys_sort(li) print(li) # 发现系统的排序比快排还要快十倍左右,其实系统的排序的时间复杂的 # 和快排、堆排、归并差不多,但是使用c写的内核,相同的代码,c的运行 # 速度是Python的十倍,所以这里也有十倍左右的差别
堆排
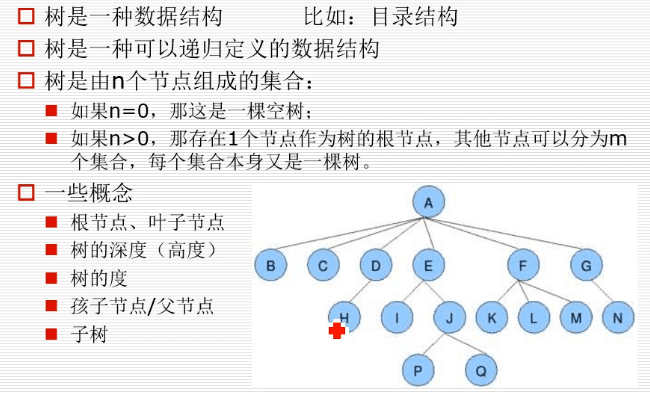
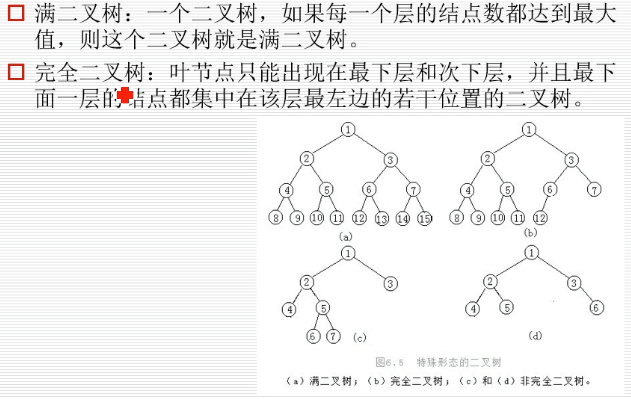
二叉树是每个节点最多有两个分叉的树:
树这种结构的数据类型其实还是存储在列表中的:可以通过父节点的索引找到两个子节点的索引,也能够通过子节点找到父节点的索引

堆是特殊的二叉树,有大根堆和小根堆之分,大根堆是是指父节点的值要大于子节点,小根堆相反
下面使用大根堆的方法进行排序:

# heap_sort堆排序 from suanfa.cal_time import cal_time def sift(li, low, high): tmp = li[low] # 原来的省长 i = low j = 2 * i + 1 while j < high: # 第二种跳出条件j < high (表示这个省长一撸到底了) if j < high and li[j+1] > li[j]: # 如果右孩子存在且大于左孩子 j += 1 if tmp < li[j]: li[i] = li[j] i = j j = 2 * i + 1 else: # 第一种跳出条件:li[j] <= tmp li[i] = tmp break else: li[i] = tmp @cal_time def heap_sort(li): n = len(li) # 1 建堆(农村包围成熟的做法,从下面村长开始,慢慢的往到省长,最后有能力的都排在上面了) for i in range(n // 2-1, -1, -1): # 最后一个非叶子节点的位置为n // 2-1 sift(li, i, n-1) # 2 挨个出数 for i in range(n-1, -1, -1): # i 表示此时堆的high位置 li[0], li[i] = li[i], li[0] # 退休+棋子 sift(li, 0, i-1) import random li = list(range(100000)) random.shuffle(li) heap_sort(li) print(li) # 上面实现的是大根堆,也可以用同样的方法,实现小根堆,Python自带的也有堆排序的模块 # 不过这个模块写的也不怎么地(能看到原码,一般pass的看不到原码的都是用c写的),并且 # 自带的只有小跟堆,使用如下: import heapq li = [6,7,4,8,5,1,9,2,3] heapq.heapify(li) print(heapq.heappop(li)) print(heapq.heappop(li)) print(heapq.heappop(li)) print(heapq.heappop(li))


# heap_test解决topK问题 # 先用Python自带的堆排序模块 import heapq li = [6,7,4,8,5,1,9,2,3,10] heapq.heapify(li) # # 依次从小到大取出一个值 # print(heapq.heappop(li)) # print(heapq.heappop(li)) # print(heapq.heappop(li)) # print(heapq.heappop(li)) # 取出前几个最大的值 print(heapq.nlargest(6, li)) # 取出前几个最小的值 print(heapq.nsmallest(6,li)) # 自己使用前面的堆排序自己写一个解决方法 # 需要将前面的自己写的大根堆改为小根堆, # 才能在这里使用 from suanfa.heap_sort import sift def topk(k, li): heap = li[0:k] for i in range(k//2 - 1, -1, -1): sift(heap, i, k-1) for i in range(k,len(li)): if li[i] > heap[0]: heap[0] = li[i] sift(heap, 0, k-1) for i in range(k - 1, -1, -1): heap[0], heap[i] = heap[i], heap[0] sift(heap, 0, i-1) print(topk(6,li))
归并排序


# merge_sort.py解决归并排序问题 from suanfa.cal_time import cal_time def merge(li, low, mid, high): i = low j = mid + 1 li_tmp = [] while i <= mid and j <=high: if li[i] < li[j]: li_tmp.append(li[i]) i += 1 else: li_tmp.append(li[j]) j += 1 while i <= mid: li_tmp.append(li[i]) i += 1 while j <=high: li_tmp.append(li[j]) j += 1 for i in range(low, high+1): li[i] = li_tmp[i-low] #给出一个两端有序的列表,使用上面的归并排序方法重新排序 li = [2,3,5,6,7,1,2,3,4,7,8] merge(li,0,4,10) print(li) # 使用上面归并排序方法解决完全乱序问题, # 使用递归,注意递归前打印和递归后打印的不同 # 这里相当于是先拆后合: def merge_sort(li, low, high): if low < high: # 要求列表中至少有两个元素 mid = (low + high) // 2 print(li[low:mid + 1], li[mid + 1:high + 1]) merge_sort(li, low, mid) merge_sort(li,mid+1,high) print(li[low:mid+1],li[mid+1:high+1]) merge(li,low,mid,high) print(li[low:high+1]) li = [10,3,4,5,2,4,7,2,5,8,3,34] merge_sort(li,0,len(li)-1) print(li)
最后综合分析一下,这几种排序问题的优缺点:


更多算法可参考:https://www.cnblogs.com/guoyaohua/p/8600214.html

作者:E-QUAL
出处:https://www.cnblogs.com/liujiajia_me/
本文版权归作者和博客园共有,不得转载,未经作者同意参考时必须保留此段声明,且在文章页面明显位置给出原文连接。
出处:https://www.cnblogs.com/liujiajia_me/
本文版权归作者和博客园共有,不得转载,未经作者同意参考时必须保留此段声明,且在文章页面明显位置给出原文连接。
本文内容参考如下网络文献得来,用于个人学习,如有侵权,请您告知删除修改。







