数值分析--第三章--迭代法

迭代一般方程：

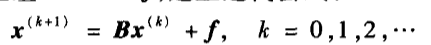
 本文实例方程组： 

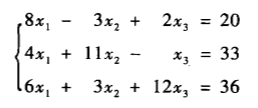
一.jacobi迭代法

从第i个方程组解出xi。

 线性方程组Ax=b，先给定一组x的初始值，如[0,0,0]，第一次迭代，用x2=0，x3=0带入第一个式子得到x1的第一次迭代结果，用x1=0,x3=0,带入第二个式子得到x2的第一次迭代结果，用x1=0,x2=0带入第三个式子得到x3的第一次迭代结果。得到第一次的x后，重复第一次的运算。

转化成一般的形式：（其中L是A的下三角部分，D是A的对角元素部分，U 是上三角部分）

 

 

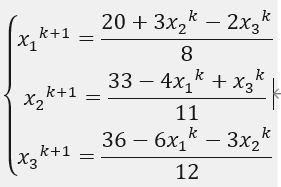
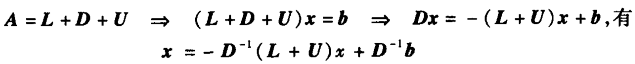
得到迭代公式：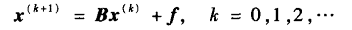

 

其中的矩阵B和向量f如何求得呢？

 

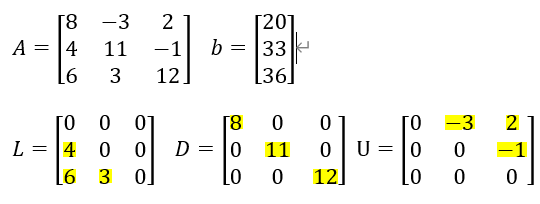
其实，矩阵B的计算也很简单，就是每行的元素/该行上的对角元素

 

 二.Gauss-Seidel迭代法【收敛速度更快】

这个可以和jacobi法对比进行理解，我们以第二次迭代为例（这里的第一次迭代结果都用一样的，懒得去换）

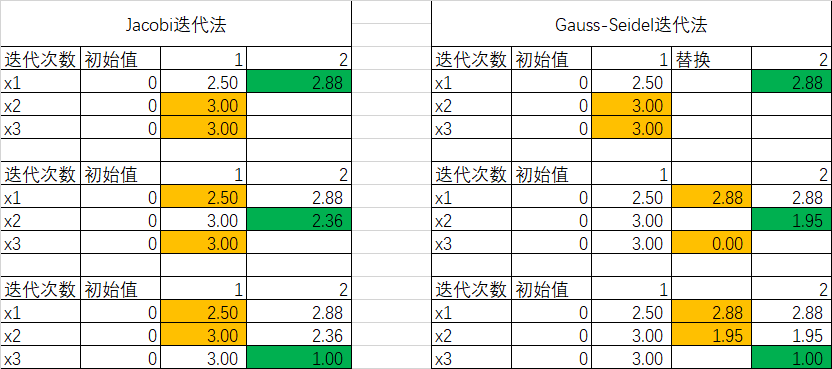
   从上表对比结果可以看出，Jacobi方法的第二次迭代的时候，都是从第一次迭代结果中，获取输入值。

上一次迭代结果[2.5,3.0,3.0]，将这个结果带入上面式子1，得到x1=2.88，；将[2.5,3.0,3.0]替换成[2.88,3.0,3.0]带入第二个式子的运算，这里得到x2=1.95，所以把[2.88,3.0,3.0]替换成[2.88,1.95,3.0]输入第三个式子计算X3=1.0.这就完成了这一次的迭代，得到迭代结果[2.88,1.95,1.0],基于这个结果，开始下一次迭代。

特点：jacobi迭代法，需要存储，上一次的迭代结果，也要存储这一次的迭代结果，所以需要两组存储单元。

  而Gauss-Seidel迭代法，每一次迭代得到的每一个式子得到的值，替换上一次迭代结果中的值即可。所以只需要一组存储单元。

 转化成一般式：

注意：第二个式子中的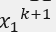是k+1次迭代的第一个式子的值，不是第k次迭代得值。

 

 

计算过程同jacobi迭代法的类似

三.逐次超松弛法SOR法

上面仅仅通过实例说明，Jacobi和Seidel迭代的运算过程。并没有构造其一般的计算公式。

Gauss-Seidel迭代法的一般公式：

.......................式1.1

 对于这个公式，怎么看着都比较别扭，分解一下就是

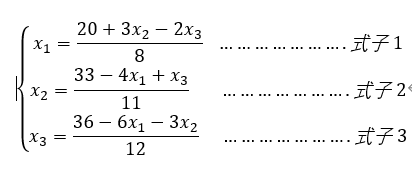
 将式1.1改写：

 .......................式1.2

同样分解一下：

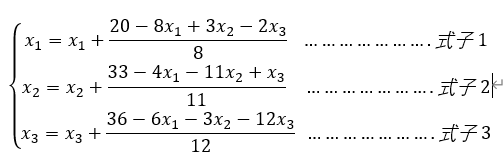
注意：左侧的x是本次（k+1）需要求的迭代结果，右侧的x是上次（k）的迭代结果。 

.......................式1.3

 .......................式1.4

分解一下：

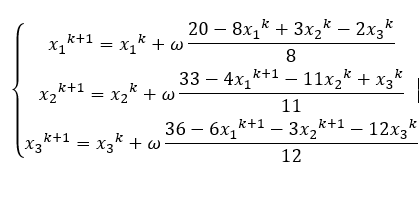
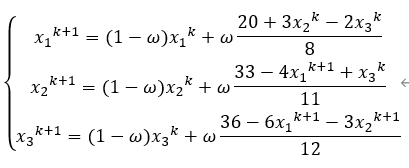
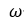松弛因子，当松弛因子=1时，就是seidel迭代法，当调节松弛因子时，可以加快或减缓迭代速度。（和深度学习中的学习因子一个意思）

 改写成矩阵形式：

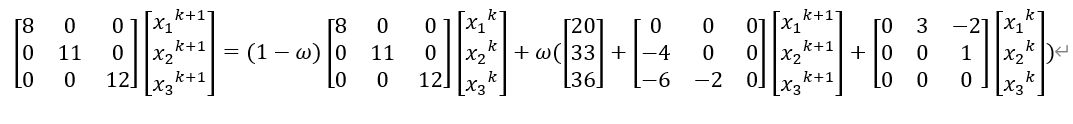
对矩阵公式进行实例化分解之后，能够直观的理解，这个公式。

四.迭代的收敛条件

从上面的实例，不断的迭代，最终可以获得需要的解。这是在给点的线性方程组的迭代方程收敛。当然，也存在不收敛的情况，最终得不到正确的解。

其中：

谱半径：

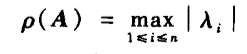
1范数：

 

 ∞范数：

 

 严格对角占优：

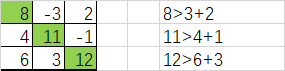
正定（顺序主子式都>0）：

 

 

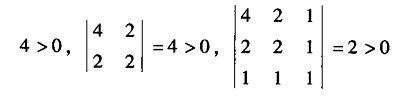
误差限：

 

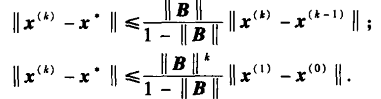
其中范数||B||<1