ensemble learning
ensemble learning（中文名：集成学习）概念介绍
集成学习这一概念，在目前各大数据挖掘竞赛中使用的非常广泛。
它的主要原理是将多个模型的决策结合起来，提高整体的预测效果。
这一概念可以进一步分类，大致可划分为：模型融合与机器学习元算法
模型融合技术：将训练出的强学习器组合起来，进一步来提高性能（常见比如：多数法（Max Voting）、平均法（Averaging Voting）、对强学习器的预测结果进行加权平均（Weighted Averaging）、对强学习器的预测结果进行再学习(Stacking，Blending)）
机器学习元算法：就是将若干个弱分类器（弱分类器可以是Knn,Logistic,DecisionTree,Logistic Regression,Bayes）通过一定策略组合成一个强分类器。（常见比如：袋装法(Bagging):{袋装通用法，随机森林法}，提升法(Boosting):{LightGBM与XGBoost})
LightGBM与XGBoost背后的原理:
1.什么是强分类器？什么又是弱分类器？
看分类器是由什么样的数据集建立的。
弱分类器一般是由整个数据集中的部分数据集建立的（基于重复抽样思想，建模时并不是完整的数据），而强分类器是由整个数据集建立的。
2.既然Bagging和Boosting都是由若分类器建立的，那么两者的区别在哪里？
看个体学习器的生成方式。
Bagging的个体学习器可以并行化生成。
Boosting的个体学习器必须串行化生成，这是因为下一个生成的模型是基于前面模型的训练结果生成的。
2.梯度下降法介绍
在机器学习任务中,我们需要让模型最终学到的参数（权重）$\theta$ ,可以让损失函数$ L(\theta )$达到最小。
因此我们需要不断地迭代,更新$\theta$的值。
那么要使$L({\theta}^{t} )<L({\theta}^{t-1})$
我们可以将$L({\theta}^{t} )$在$L({\theta}^{t-1} )$处进行泰勒展开：
令：$ {\theta}^{t}={\theta}^{t-1}+\Delta \theta $
$L({\theta}^{t} )= L({\theta}^{t-1}) + {L}^{'}({\theta}^{t-1})\Delta \theta$
令： $\Delta \theta = -\alpha \times {L}^{'}({\theta}^{t-1})$，则上述式子变为了：
$L({\theta}^{t} )= L({\theta}^{t-1}) -\alpha \times {({L}^{'}({\theta}^{t-1}))}^{2}$，则这里的$\alpha$就是我们常说的学习率（注：一般工具包的内部对这一过程封装了）
3.当弱分类器变多了，我们同样可以将梯度下降法用到Boosting算法上：
我们假设第一个分类器损失函数为$f_{0}(x)$
那么当我们用多个分类器去预测时损失函数可以写成这个样子
$f^{t}(x)=f^{t-1}(x)+\Delta f_{t}(x)$
这样我们借助于梯度下降的思想，同样可以找到这样的$\Delta f_{t}(x)$
$\Delta f_{t}(x)= -\alpha_{t} \times g_{t}(x)$, $g_{t}(x)$为第t次函数的一介导数。
4.当弱分类器是CART回归树时
假设数据集D={（x1,y1），（x2,y2），...，}
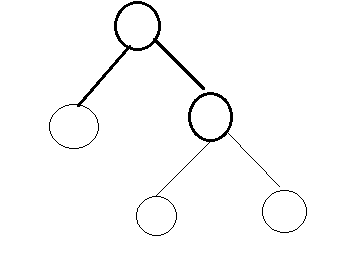
当一个回归树时上述形状时，其实是将原始的数据集按照特征拆分成m个特征空间，m为叶子节点的个数。
则$F(x)=\sum_{m=1}^{M} c_{m}I (x ∈ R_{m})$,I为指示函数，属于为1，不属于为0，其中第m个叶子节点得到的预测值我们记为cm
假设回归树的某个叶子节点的Loss_Function可写成：
$L(c_{m})=\sum_{k=1}^{k}(y_{i} - F(x_{i}))^{2}$，k为第k个样本。
对其求导致可知，可知cm=(y1+y2+...+yk)/k时，$L(c_{m})$取得极小值。
也就是对于第m个叶子节点来说，$L(c_{m})=\sum_{k=1}^{k}(y_{i} - c_{m})^{2}$
那么如何保证每一次划分节点时，总体的loss值最小呢？
我们需要保证在每一次划分节点后，得到的两个子树loss最小（为未分裂前的叶子节点叫子树），那么用数学语言可以是这个样子：
（***step_1***）
得到cn=
。N代表该子树下样本的个数，j代表用最优切分变量，s代表切分点。（***step_2**）
切分后是这个样子：
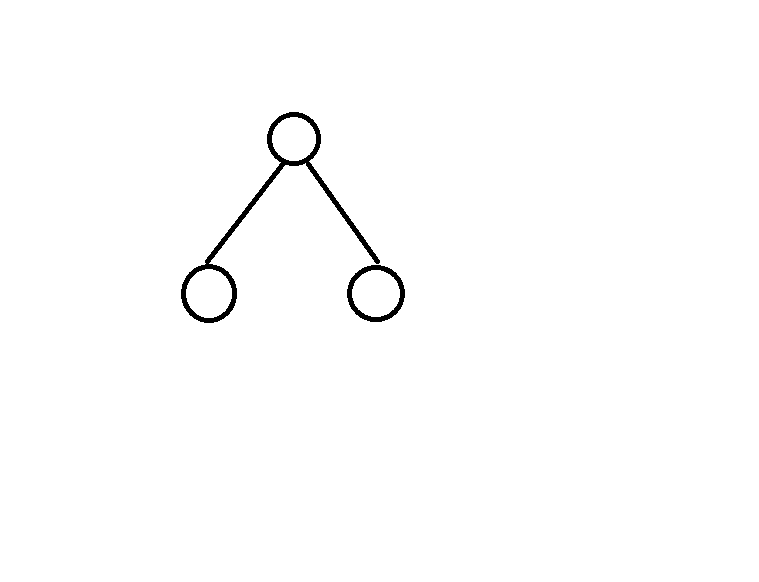
继续对以上两个子区域调用步骤一和步骤二，直至满足停止条件（比如叶子节点的样本数量是多少，树的深度是多少，使用了多少个特征）。
最终达到停止条件后，将输入空间分为M个区域 $R_{1}，R_{2},......R_{n})$，也就是M个节点，生成决策树：
$F(x)=\sum_{m=1}^{M} c_{m}I (x ∈ R_{m})$
5.GBDT的算法原理：
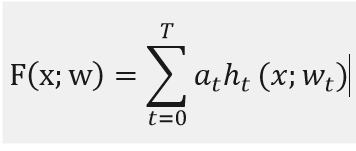
我们定义F为加法模型，x为输入样本，h为分类回归树，w是分类回归树的参数。a是每棵树的权重。
那么我们定义F*为此加法模型的损失函数，这样我们得到的就是上述损失函数的极小值。
整个GBDT的迭代过程如下：
| 输入:样本点$(x^{i},y^{i})$,迭代总数T,损失函数L |
| 1.对于t=0来说，初始化f0 |
| 2.for t=1 to T do |
| 2.1:计算偏导数，找第t-1棵树的损失函数最优点（换句话说寻找t-1棵树残差的最小值点）：$y_{i}^{\dot{}}=-\frac{\partial L(y_{i},F(X_{i}))}{\partial F(X_{i})},I=1,2,...,N$ |
| 2.2:学习第t棵树，寻找最优参数w：$w^{*}=arg min\sum_{i=1}^{N}(y_{i}^{*}-h_{t}(x_{t};w))^{2}$ |
|
2.3:与前面介绍的梯度下降法一样，寻找到我们的$\Delta f_{t}(x)$ $p^{*}=argmin \sum_{i=1}^{N}L(y_{i},(F_{t-1}(x_{i}) +p\times h_{t}(x_{t};w)))$ |
|
2.4:令 $f_{t}=p^{*}h_{t}(x_{t};w)$ |
| 3.更新模型：$F_{t} = F_{t-1} + f_{t}$ |
| 4.输出模型：$F_{t}$ |
6.LightGBM算法之改进:
LightGBM算法与XGBoost算法对于同样的实验来说，准确率相当，而lgb的内存占用更少，并且运行速度更快。
这其中原因在于LightGbm背后采用了直方图算法，且节点切分相比xgboost采用了“leaf-wise”方法。
