一道考题---当n=1,2,3...2015时,统计3n+n3能整除7的个数

当n=1,2,3...2015时,统计3ⁿ+n³能整除7的个数。

编程解法：

#include <iostream>
#include <cmath>
using namespace std;

int mod_pow(int  c , int  d , int  n)
{
    int res=1;
    while(d>0){
        if(d&1)
            res=res*c%n; 
      	c=c*c%n;
		d>>=1;
    }  
    return res;
}

int main(){
	int i=1;
	int sum=0,count=0;
	for(i;i<=2015;i++){
		sum=0;
		sum+=mod_pow(3,i,7);
		int temp=i%7;
		sum+=(temp*temp*temp)%7;
		sum%=7;
		if(sum==0) count++;
	}
	cout<<count;   
	return 0;
}

　　得个数为288.

其实本题考查的是数学同余的知识，重点在于同余的分析。编程解法只是验证下同余解法是否正确。

下面是同余解法：  由(a+b)%c = (a%c+b%c)%c,分析，我们可以分别讨论n³和3ⁿ被7整除的情况

首先分析n³被7整除的余数的规律：

令n=7m+a  (m为正整除，a=0,1,2...6)

则n³ = (7m+a)³=7m(7m+a)²+a(7m+a)² = 7m(7m+a)²+a(7m+a)(7m+a) = 7m(7m+a)²+a*7m(7m+a)+a²(7m+a) = 7m(7m+a)²+a*7m(7m+a)+7ma²+a³

因此我们只需要看a³被7整除的余数即可.

当a=0时，a³ = 0  = 7* 0 + 0 n³被7整除，余数为 0
当a=1时，a³ = 1  = 7* 0 + 1, n³被7整除，余数为 1
当a=2时，a³ = 8  = 7* 1 + 1, n³被7整除，余数为 1
当a=3时，a³ = 27 = 7* 3 + 6, n³被7整除，余数为 6
当a=4时，a³ = 64 = 7* 9 + 1, n³被7整除，余数为 1
当a=5时，a³ = 125= 7*17 + 6, n³被7整除，余数为 6
当a=6时，a³ = 216= 7*30 + 6, n³被7整除，余数为 6
因此，n³ 被7整除的余数规律为　周期为7的数：1、1、6、1、6、6、0

 

接下来分析3ⁿ被7整除的余数的规律.

n=1  3ⁿ  被7整除的余数为3
n=2  3ⁿ  被7整除的余数为2
n=3  3ⁿ  被7整除的余数为6
n=4  3ⁿ  被7整除的余数为4
n=5  3ⁿ  被7整除的余数为5
n=6  3ⁿ  被7整除的余数为1
n=7  3ⁿ  被7整除的余数为3
n=8  3ⁿ  被7整除的余数为2
n=9  3ⁿ  被7整除的余数为6
n=10 3ⁿ  被7整除的余数为4
n=11 3ⁿ  被7整除的余数为5
n=12 3ⁿ  被7整除的余数为1

因此，3ⁿ 被7整除的余数规律为　周期为6的数：3、2、6、4、5、1

 

分析n³被7整除的余数的周期为7,分别为1、1、6、1、6、6、0

     3ⁿ被7整除的余数的周期为6，分别为3、2、6、4、5、1

则n³ + 3ⁿ 被7整除的周期起码6*7=42.    42中情况中有6钟情况下二者之和能被7整除，如下表.

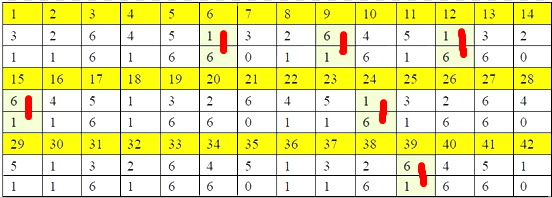
又有2015 = 42*47+41  ,即有47个周期+41个数(如表最后一个不能被7整除，也就不是6个钟的1个，所以后41个数中也有6个能被7整除),所以能被7整除的数就有47*6+6=288个.