树的深度优先搜索(下)
树的深度优先搜索(下):如何才能高效率地查字典?
从数学的思想,到最终的编程实现,其实需要一个比较长的流程。我们首先需要把问题转化成数学中的模型,然后使用数据结构和算法来刻画数学模型,最终才能落实到编码。
如何使用递归和栈实现深度优先搜索?
什么样的编程方式可以实现对树结点和边的操作?
深度优先搜索的过程和递归调用在逻辑上是一致的。
我们可以把函数的嵌套调用,看作访问下一个连通的结点;把函数的返回,看作没有更多新的结点需要访问,回溯到上一个结点。
第一种情况:被查单词所有字母都被处理完毕,但是我们仍然无法在字典里找到相应的词条。
每次递归调用的函数开始,我们都需要判断待查询的单词,看看是否还有字母需要处理。如果没有更多的字母需要匹配了,那么再确认一下当前匹配到的结点本身是不是一个单词。如果是,就返回相应的单词解释,否则就返回查找失败。对于结点是不是一个单词,你可以使用 Node 类中的 explanation 变量来进行标识和判断,如果不是一个存在的单词,这个变量应该是空串或者 Null 值。
第二种情况:搜索到前缀树的叶子结点,但是被查单词仍有未处理的字母,就返回查找失败。
通过结点对象的 sons 变量来判断这个结点是不是叶子结点。如果是叶子结点,这个变量应该是空的 HashMap,或者 Null 值。
第三种情况:搜索到中途,还没到达叶子结点,被查单词也有尚未处理的字母,但是当前被处理的字母已经无法和结点上的 label 匹配,返回查找失败。是不是叶子仍然通过结点对象的 sons 变量来判断。
查找一个单词的过程,其实就是在有向树中,找一条从树的根到代表这个单词的结点之通路。那么如果要遍历所有的单词,就意味着我们要找出从根到所有代表单词的结点之通路。所以,在每个结点上,我们不再是和某个待查询单词中的字符进行比较,而是要遍历该结点所有的子结点,这样才能找到所有可能的通路。我们还可以用递归来实现这一过程。
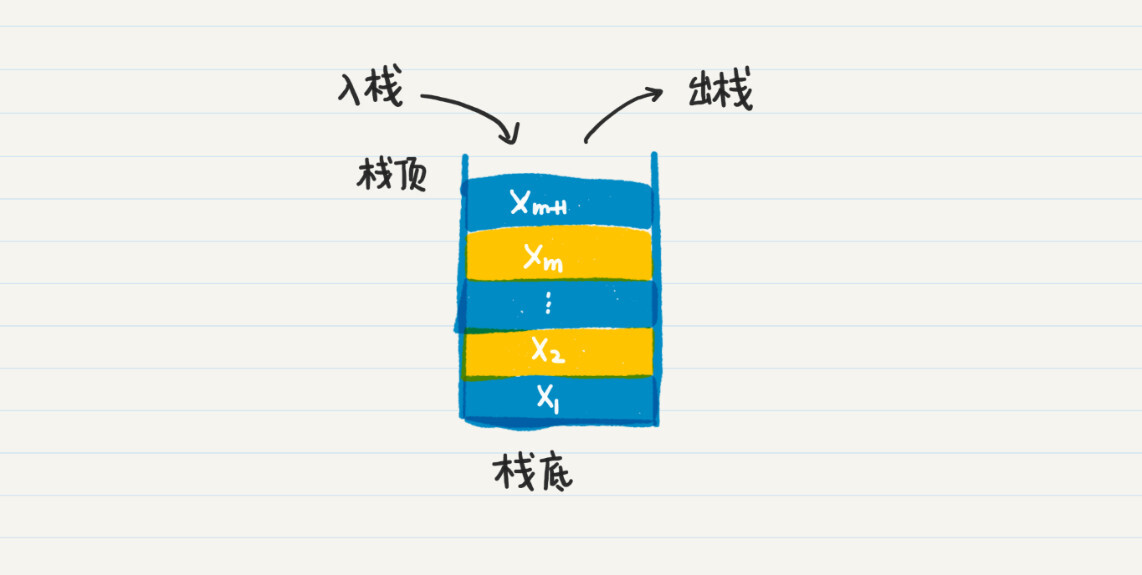
栈的特点是先进后出(First In Last Out),也就是,最先进入栈的元素最后才会得到处理。
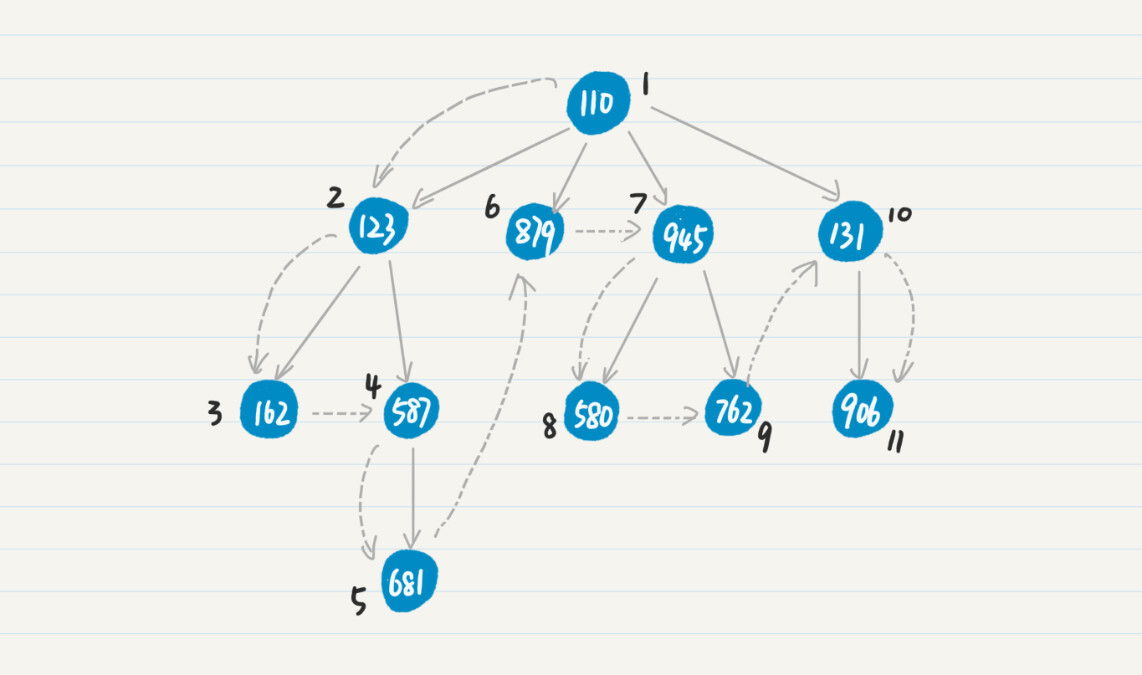
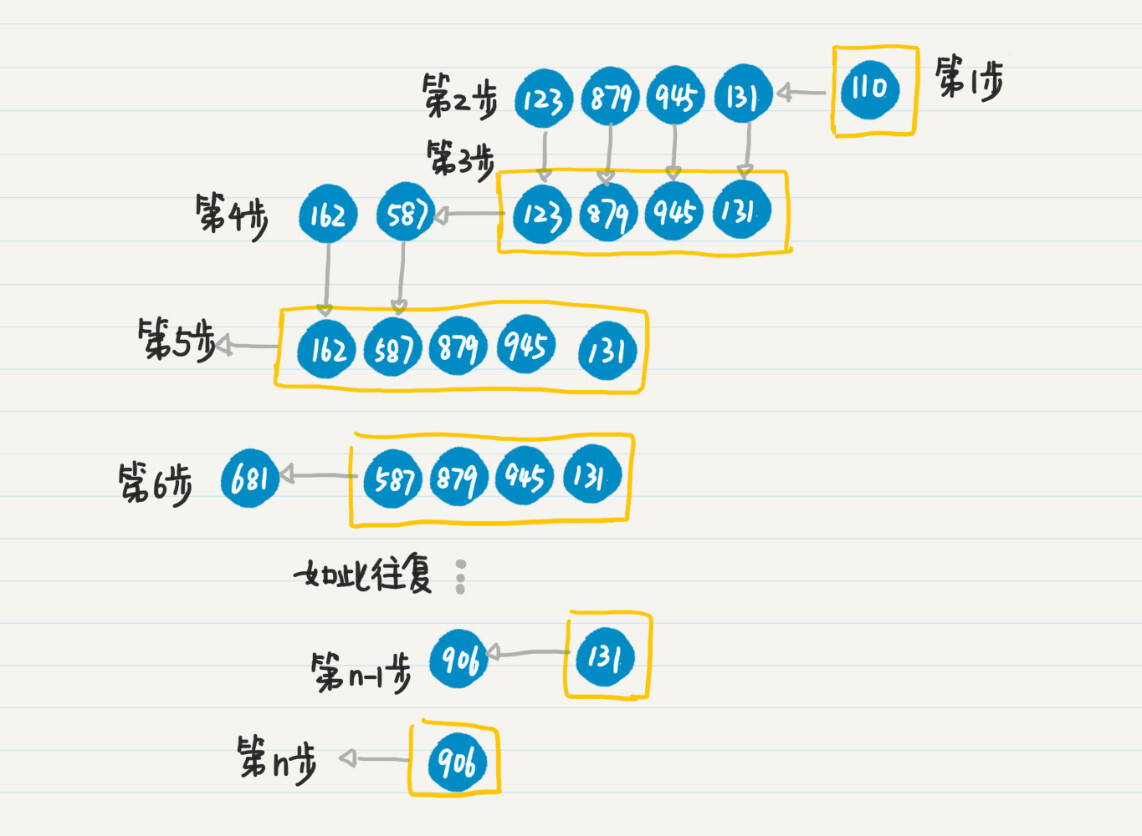
第 1 步,将初始结点 110 压入栈中。
第 2 步,弹出结点 110,搜出下一级结点 123、879、945 和 131。
第 3 步,将结点 123、879、945 和 131 压入栈中。
第 4 步,重复第 2 步和第 3 步弹出和压入的步骤,处理结点 123,将新发现结点 162 和 587 压入栈中。
第 5 步,处理结点 162,由于 162 是叶子结点,所以没有发现新的点。第 6 步,重复第 2 和第 3 步,处理结点 587,将新发现结点 681 压入栈中。
……
第 n-1 步,重复第 2 和第 3 步,处理结点 131,将新发现结点 906 压入栈中。
第 n 步,重复第 2 和第 3 步,处理结点 906,没有发现新的结点,也没有更多待处理的结点,整个过程结束。
计算机系统里的函数递归,在内部也是通过栈来实现的。如果我们不使用函数调用时自动生成的栈,而是手动使用栈的数据结构,就能始终保持数据的副本只有一个,大大节省内存的使用量。
当我们把某个结点的子结点压入栈的时候,由于栈“先进后出”的特性,会导致子结点的访问顺序,和递归遍历时子结点的访问顺序相反。如果你希望两者保持一致,可以用一个临时的栈 stackTemp 把子结点入栈的顺序颠倒过来。
总结
在归并排序的数据分解阶段,初始的数据集就是树的根结点,二分之前的数据集代表父节点,而二分之后的左半边的数据集和右半边的数据集都是父结点的子结点。分解过程一直持续到单个的数值,也就是最末端的叶子结点,很明显这个阶段可以用树来表示。如果使用递归编程来进行数据的切分,那么这种实现就是深度优先搜索的体现。
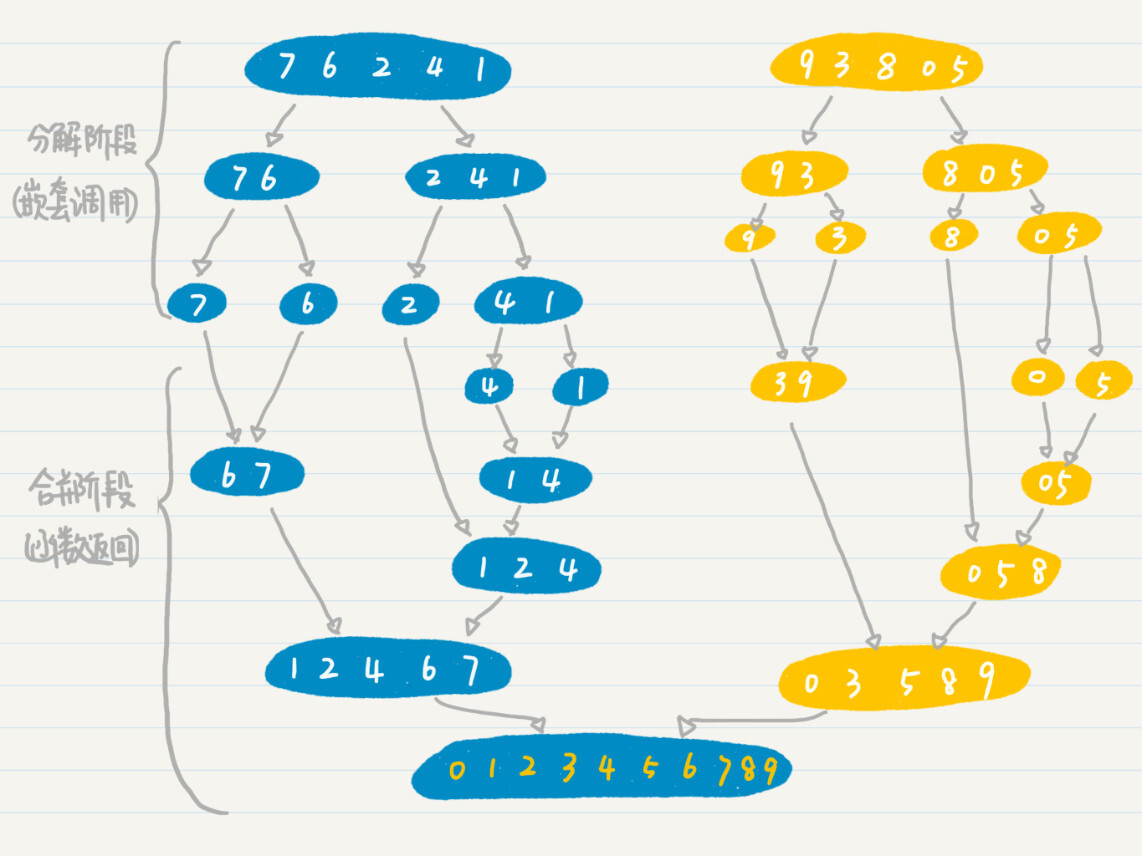
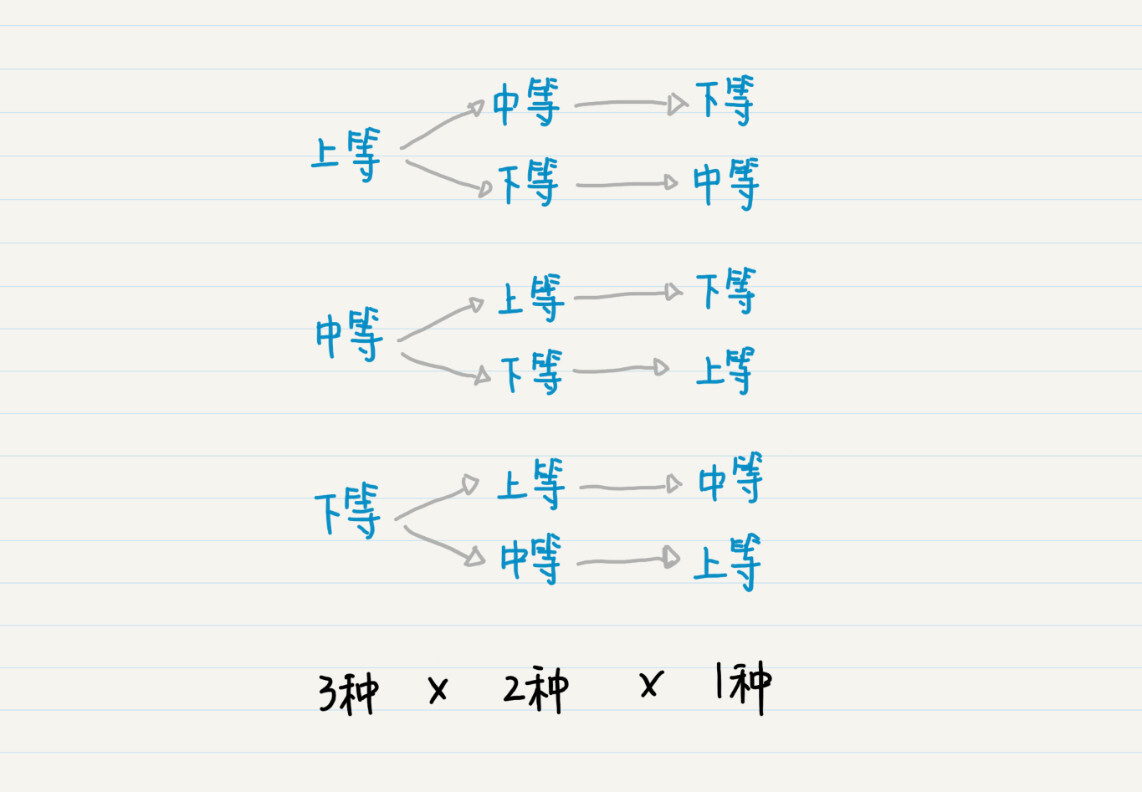
在排列中,我们可以把空集认为是树的根结点,如果把每次选择的元素作为父结点,那么剩下可选择的元素,就构成了这个父结点的子结点。而每多选择一个元素,就会把树的高度加 1。因此,我们也可以使用递归和深度优先搜索,列举所有可能的排列。
深度优先搜索的核心思想,就是按照当前的通路,不断地向前进,当遇到走不通的时候就回退到上一个结点,通过另一个新的边进行尝试。如果这一个点所有的方向都走不通的时候,就继续回退。这样一次一次循环下去,直到到达目标结点。树中的每个结点,既可以表示某个子问题和它所对应的抽象状态,也可以表示某个数据结构中一部分具体的值。




