基于离散对数的签名方案
基于离散对数的签名方案
ElGamal对其进行了研究,提出了著名的ElGamal数字签名方案,该方案的修正形式被美国国家标准技术研究所(NIST)作为数字签名标准。
- ElGamal签名体制
(1)参数设置
① 随机选择大素数p,且要求p-1有大素因子,g是的生成元。
② 随机选取一个整数x(1<x<p-1),计算
y=g^xmodp
公钥:k1=(y,g,p)
私钥:k2=x
(2)签名过程
消息m,签名者选择随机整数k,1<k<p-1,计算:
r=gkmodp,s=(h(m)-xr)k-1mod(p-1)
则签名为(r,s)
(3)验证过程
接收者B收到m和(r,s)后,先计算h(m),然后验证灯饰:
yr*rsmodp=g^h(m)modp
=>Ver=True
k在签名中用到,验证中用不到,故不需也不能公开。
s值在验证中是放在指数上的,故计算中模运算是mod(p-1)
k值随机取,同一个消息m不同的k,签名值不同;不同的消息m不同的k,签名值可能有相同,增加了攻击的难度。
RSA签名中,同一个消息的签名相同,容易被攻击。
签名中对消息m的Hash值进行的签名,如果不使用Hash函数直接对m进行签名,可以伪造签名攻击。
(4)正确性证明
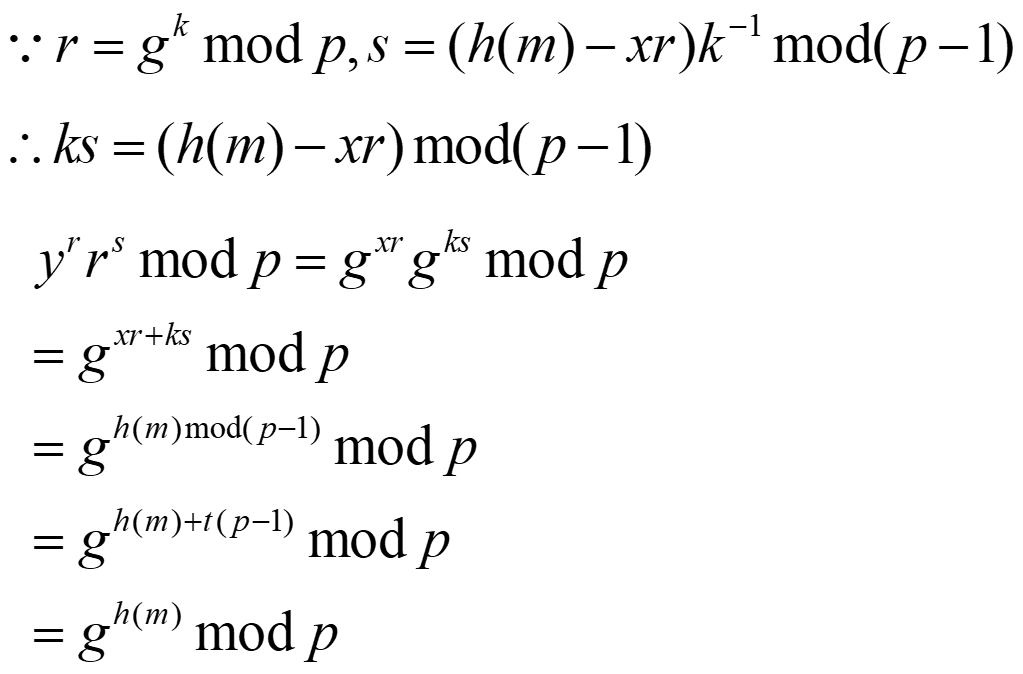
例 (1)参数选取:p=19,生成元g=2,x=15,h(m)=16,
计算y=gxmodp=215mod19=12
公钥:k1=(p,g,y)=(19,2,12)
私钥:k2=x=15
(2)签名:选取随机数k=11,计算:
r=gkmodp=211mod19=15,
kk-1mod(p-1)=11k-1mod18=1,k^-1=5(可穷举)
s=(h(m)-xr)k^-1mod(p-1)=(16-1515)*5mod18=17
签名为(r,s)=(15,17)
(3)验证
yr*rsmodp=1215*1517mod19=5
gh(m)modp=216mod19=5
Ver=True
(4)安全性分析
① k值不能泄露
s=(h(m)-xr)*k^-1mod(p-1)
x=(h(m)-sk)r^-1mod(p-1)
k值泄露可计算出私钥x。
② k值不能重复使用
设签名者对发送给A的m1、B的m2使用相同的k进行签名,为(r,s1),(r,s2)。
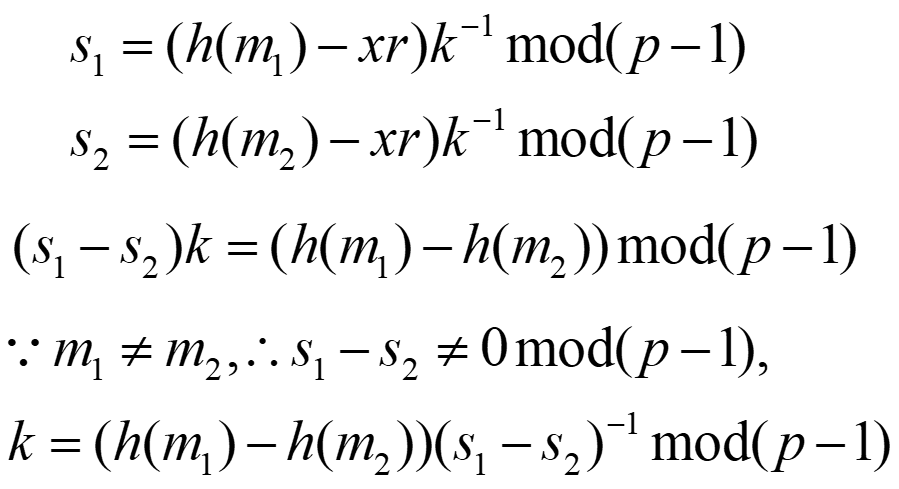
所以A、B一单联手,可求出k,从而可求出私钥x。
③ 多次签名所使用的k应无关联
④ 不使用Hash函数,则签名方案容易受到攻击



