基于RSA的签名方案
基于RSA的签名方案
Hash函数签名
s=m^dmodn 计算量太大,实际情况是对m利用一个安全的公开的Hash函数来产生消息摘要h(m),然后计算签名:
s=[h(m)]^dmodn
验证过程为:
s^emodn=h(m)=>Ver=True
优点:
①计算更快;
②原有方案可被攻击,新方案无法攻击。
Hash函数也称为散列函数、杂凑函数,它是一种将任意长度的输入变换为固定长度输出的不可逆的单向函数,并且没有陷门。
(1)Hash函数结构
Hash函数一般采取迭代压缩结构,将输入消息分为L个固定长度的分组,每个分组长bbit,最后一个分组包含输入消息的总长度,若最后一个分组不足bbit,可用全0或全1序列填充为bbit。

其中的f函数通常是复杂的非线性函数关系,由其实现单向性。
注:Hash函数主要有:MD4、MD5、SHA1、SHA256、SHA512等。
(2)要求
①Hash函数可应用于任意长度的消息,产生定长的输出;(至少是160bit)
②对于消息x,计算h(x)容易,但由h(x)值求x在计算上是不可行的,(此称为单向性)
(所谓计算上不可行是指:理论上存在x,但是无法找到有效的方法计算出,只能穷举。)
③抗碰撞性:无法找到两个消息x≠y,但h(x)=h(y)。
(h(x)是多对一函数,但到目前为止,未出现过一次碰撞,即使意外的情况也没有。)
例 选取参数p=13,q=11,e=13,h(m)=16,进行签名并验证。
解:(1)参数
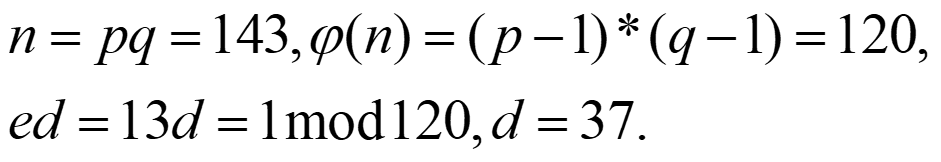
则公钥:k1=(e,n)=(13,143)
私钥:k2=d=37
(2)签名
S=[h(m)]dmodn=1637mod142=3
(3)验证
semodn=313mod143=16=h(m)
所以Ver=True



