数字签名的实现方案
数字签名的实现方案
基于RSA的签名方案
方案的原理:
签名者使用自己的私钥对待签名消息m进行签名(加密),然后将m和密文发送给接收者,接收者使用签名者的公钥进行验证(解密)。签名验证过程与RSA加解密过程相似。
- 方案
(1)参数设置
① 任取两个大素数p和q;
② 计算n=p*q(注:此时n只有唯一一种分解方法),
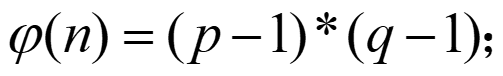
③ 随机选取整数e,满足:
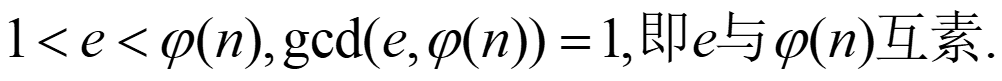
④ 用欧几里得扩展算法计算d,满足:
⑤ 公开密钥(公钥): k1=(e,n)
私有密钥(私钥):k2=(p,q,d)
(2)签名(即加密过程)
对于待签名消息m,签名:
s=m^dmodn
(3)验证过程(即解密过程)
s^emodn=m ==> Ver=True
(4)正确性证明
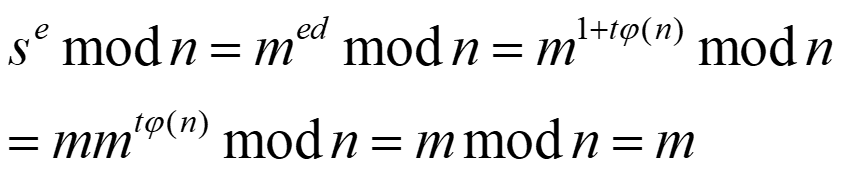
- 签名与加密的结合
设A:签名者、发送者 B:接收者、验证者
方法一:
对于明文m,A利用自己的私钥计算签名s,将(m,s)利用B的公钥加密为(cm,cs),然后将(cm,cs)发送给B,B接收后利用自己的私钥解密得到(m,s),再利用A的公钥进行验证;
方法二:
明文m,A利用B的公钥加密得到c,对c进行签名为s,将(c,s)发送给B,B接收后利用A的公钥进行验证,验证通过后再利用自己的私钥进行解密得到m。
注:方法二有缺点,可被伪造签名,一般使用方法一。
窃听者H窃取到A发给B的(c,s),H将密文c用自己的私钥和签名算法进行签名得签名s',然后将(c,s')发给B,B接收后发现是H发送的,则B利用H的公钥进行验证C确实是H发送的,B再用自己的私钥解密c得明文m,则B误认为明文m是H发送给B的。
(例如招标标底的提交。)
- Hash函数签名
前述签名中s=m^dmodn计算量太大,实际情况是对m利用一个安全的公开的Hash函数来产生消息摘要h(m),然后计算签名:
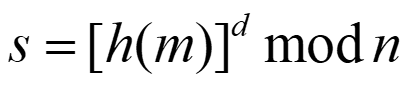
验证过程为:
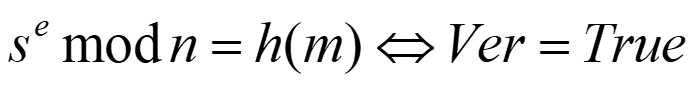
优点:
①计算更快;
②原有方案可被攻击,新方案无法攻击。
Hash函数也称为散列函数、杂凑函数,它是一种将任意长度的输入变换为固定长度输出的不可逆的单向函数,并且没有陷门。



