数学归纳法
数学归纳法:如何用数学归纳提升代码的运行效率?
“归纳”,是一种从经验事实中找出普遍特征的认知方法。

- 通过上面的表格,我们可以进行归纳,并得出这样的结论:
- 如果一个动物,身上长羽毛并且会飞,那么就是属于鸟;
- 如果一个动物,身上长绒毛、不会飞、而且吃小鱼和老鼠,那么就属于猫。
什么是数学归纳法?
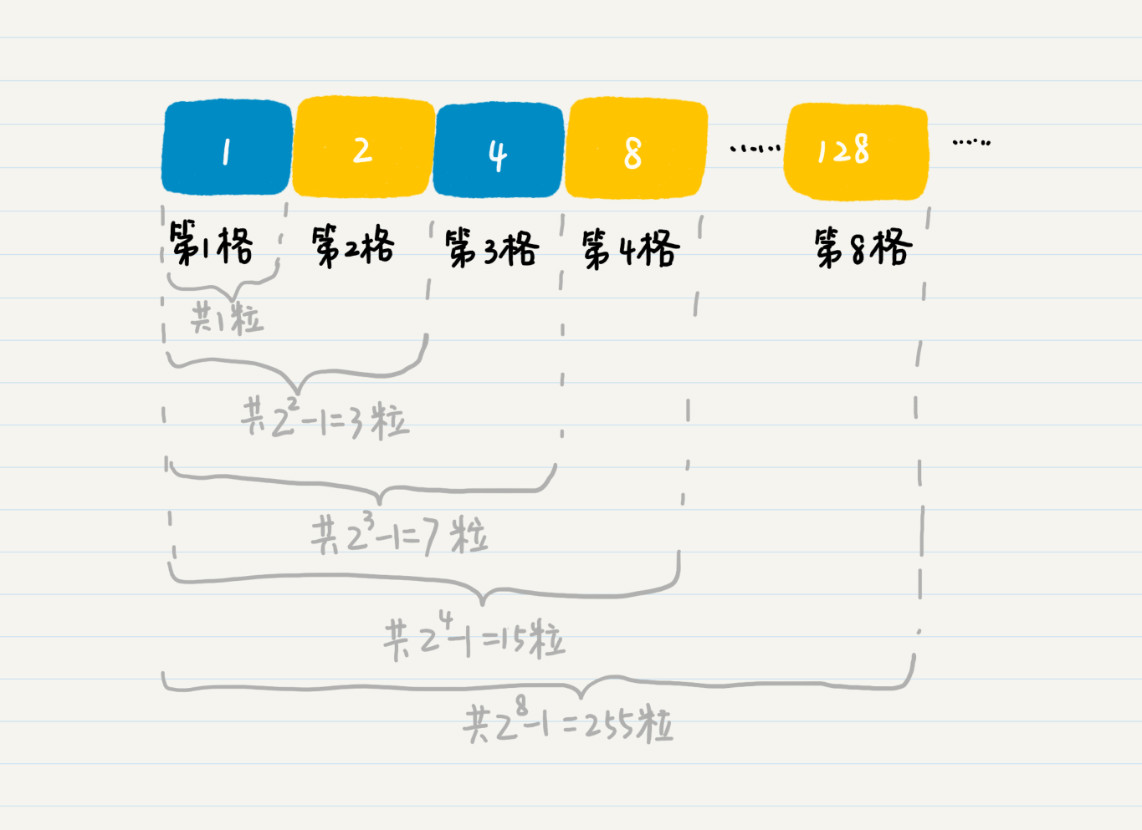
根据这个观察,我们是不是可以大胆假设,前 n 个格子的麦粒总数就是 2^{n}-1 呢?如果这个假设成立,那么填满 64 格需要的麦粒总数,就是 1+2+2{2}+2+2^{4}+……+ 2^{63}
=2^{64}-1=18446744073709551615。
数学归纳法的一般步骤是这样的:
证明基本情况(通常是 n=1 的时候)是否成立;
假设 n=k-1 成立,再证明 n=k 也是成立的(k 为任意大于 1 的自然数)。
第一个子命题是,第 n 个棋格放的麦粒数为 2^{n-1}。第二个子命题是,前 n 个棋格放的麦粒数总和为 2^{n}-1。
基本情况:我们已经验证了 n=1 的时候,第一格内的麦粒数为 1,和 2^{1-1} 相等。因此,命题在 k=1 的时候成立。
假设第 k-1 格的麦粒数为 2^{k-2}。那么第 k 格的麦粒数为第 k-1 格的 2 倍,也就是 2^{k - 2}*2=2^{k-1}。因此,如果命题在 k=n-1 的时候成立,那么在 k=n 的时候也成立。
基本情况:我们已经验证了 n=1 的时候,所有格子的麦粒总数为 1。因此命题在 k=1 的时候成立。
假设前 k-1 格的麦粒总数为 2^{k-1}-1,基于前一个命题的结论,第 k 格的麦粒数为 2^{k-1}。那么前 k 格的麦粒总数为 (2{k-1}-1)+(2)=2*2{k-1}-1=2-1。因此,如果命题在 k=n-1 的时候成立,那么在 k=n 的时候也成立。
和使用迭代法的计算相比,数学归纳法最大的特点就在于“归纳”二字。它已经总结出了规律。只要我们能够证明这个规律是正确的,就没有必要进行逐步的推算,可以节省很多时间和资源。
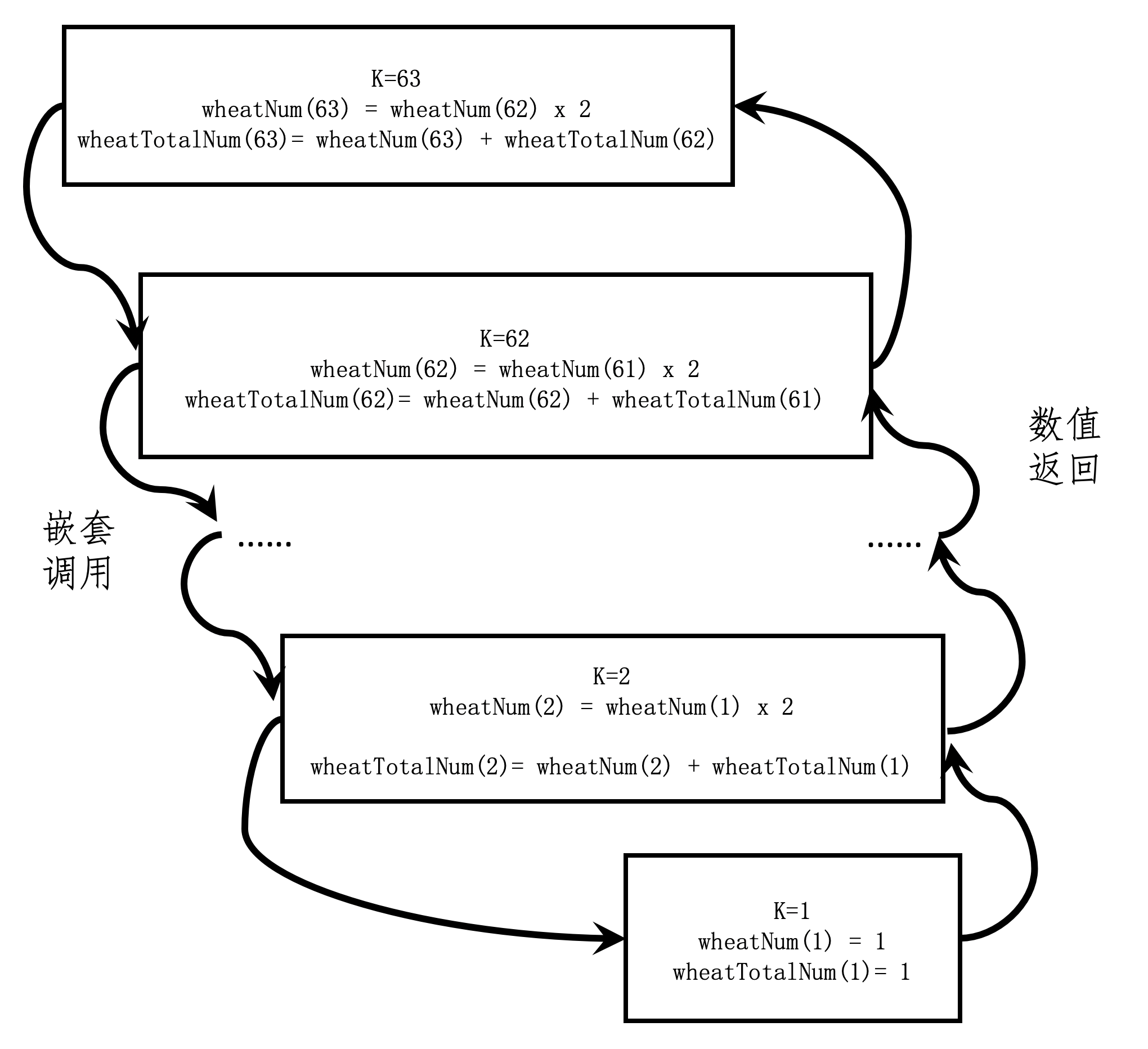
从这个图可以看出,函数从 k=63 开始调用,然后调用 k-1,也就是 62,一直到 k=1 的时候,嵌套调用结束,k=1 的函数体开始返回值给 k=2 的函数体,一直到 k=63 的函数体。从 k=63, 62, …, 2, 1 的嵌套调用过程,其实就是体现了数学归纳法的核心思想,我把它称为逆向递推。而从 k=1, 2, …, 62, 63 的值返回过程,和上一篇中基于循环的迭代是一致的,我把它称为正向递推。
总结
数学归纳法在理论上证明了命题是否成立,而无需迭代那样反复计算,因此可以帮助我们节约大量的资源,并大幅地提升系统的性能。
数学归纳法实现的运行时间几乎为 0。不过,数学归纳法需要我们能做出合理的命题假设,然后才能进行证明。




