线性移位寄存器(LFSR)
线性移位寄存器(LFSR)
定义
- 一个n级寄存器是一个由n个存储单元b1,b2,……,bn和一个计算单元f(b1,b2,……,bn)构成的装置,
bn+1=f(b1,b2,……,bn)
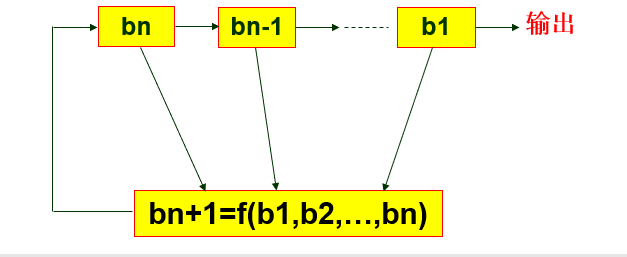
若f为线性函数
f(b1,b2,……,bn)=t1b1+t1b2+……+tn*bn
称为线性反馈寄存器,即为LFSR
其中ti=0,1,ti的作用相当于一个开关,用断开和闭合来表示0和1.

例n=3,f(b1,b2,b3)=b1+b3,则输入101,
则输出为:101001110100111010011……
周期T=7=2^3-1
LFSR周期
- 寄存器上始终存储着n个元素,该n个元素称为一个状态,初始时刻的状态为:
- S1=(b1,b2,……,bn)
第i时刻的状态为:
Si=(bi,bi+1,……,bi+n-1)
在n级条件下,最多有2n个状态,而在线性运算下,全0不会转入其他状态,故LFSR序列的最长周期为:2n-1
m序列
定义:
- 当n级LFSR序列{bi}的周期T=2^n-1时,称{bi}为n级m序列。
注:如何选择合适的反馈函数LFSR使得序列周期达到最大(m序列),是研究重点。
m序列的产生
- 特征多项式
- 若LFSR序列{bi}满足bn+1=t1b1+t2b2+……—+tnbn,令p(x)=1-t1x+t2x2+……+tnxn (t0=1)称p(x)为LFSR的特征多项式
Th
- LFSR序列{bi}为n级m序列的充要条件是其特征多项式p(x)是本原多项式。
注1:本原多项式概念略。
注2:n次本原多项式的个数:
Matlab中调用本原多项式的命令:
primpoly(n,'all')
常用本原多项式
x^2+x+1
x^3+x+1
x^4+x+1
x^5+x^2+1
x^6+x+1
x^7+x^3+1
x^8+x^4+x^3+x^2+1
x^9+x^4+1
x^10+x^3+1
x^11+x^2+1


