分组密码
分组密码
概述
- 所谓分组密码,简单地说就是对明文进行分组,每组的长度都相同,然后对每组明文使用密钥进行加密得密文,解密即对每组明文使用密钥进行解密得到明文。
- 通常情况是明文、密文等长。(好处是处理速度快,节约了存储,避免了浪费带宽.)
- 定义
- 分组密码包含5个部分{M,C,K,E,D},
- M=F(2,n)明文空间
- K=F(2,k)密钥空间
- C=F(2,n)密文空间
- E加密变换;
- D解密变换
明文m1m2……mn通过密钥k加密算法得到密文c1c2……cn
分组密码是一种映射: - E:M*K->C
- D:C*K->M
- 注:分组密码实际上是{0,1,2,……,2^n-1}到其自身的一一映射,密钥k不同映射不同。
- 基本要求
- 分组长度足够长(防止明文穷举攻击)
- 密钥长度足够长(防止密钥穷举攻击)
- 加解密算法要足够复杂(能抗击各种已知攻击)
- 分组密码的原则
为有效抵抗对密码体质的通知分析,香农提出了两个原则:扩展原则和混乱原则。
- 扩散:指每1bit明文的变化尽可能多地影响密文序列的bit,以隐蔽明文的统计特性,防止对密钥进行逐段攻击破译;
- 混乱:指加密变换过程中明文、密钥以及密文之间的关系尽可能的复杂,以防止破译者采用统计分析方法进行攻击。
- 分组密码的结构(SP网络)
-
需求分析:
- 一个分组密码既要难于分析(复杂),又要易于实现(简单),迭代密码可克服这一对矛盾。其加密变换一般采取如下结构:
- 由一个简单的函数F(易于实现)迭代若干次而形成。
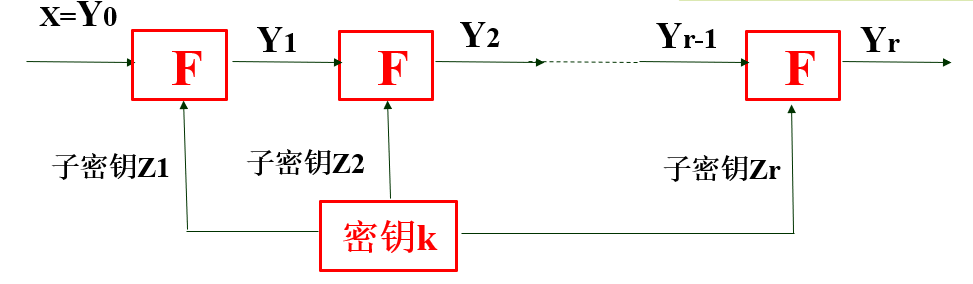
-
其中Yi-1是第i轮迭代的输入,Yi是第i轮的输出,Zi由密钥k导出,这类密码即迭代密码。如DES是16轮迭代密码,多次迭代可实现必要的混乱与扩散。
-
F函数采用代换置换结构,置换由P盒实现,起扩散作用,代换可提供混淆作用,其中代换被精心设计且起关键作用,人们常称其为“黑盒子”。
-
SP结构具有雪崩效应,雪崩效应指输入(明文或密钥)即使只有很小的变化,也会导致输出(密文)产生巨大的变化。


