密码学概述&置换密码

密码学

概述

如何将信息进行加密，传送到接收方，接收方在进行解密获取信息，中间即使有窃听者窃听到信息也可解密破解。

密码学分类

1. 密码编辑学(保密)
2. 密码分析学(破译)

• 该破译与传统的黑客技术有一定的区别

传统密码体质

1. 密码系统图示
   

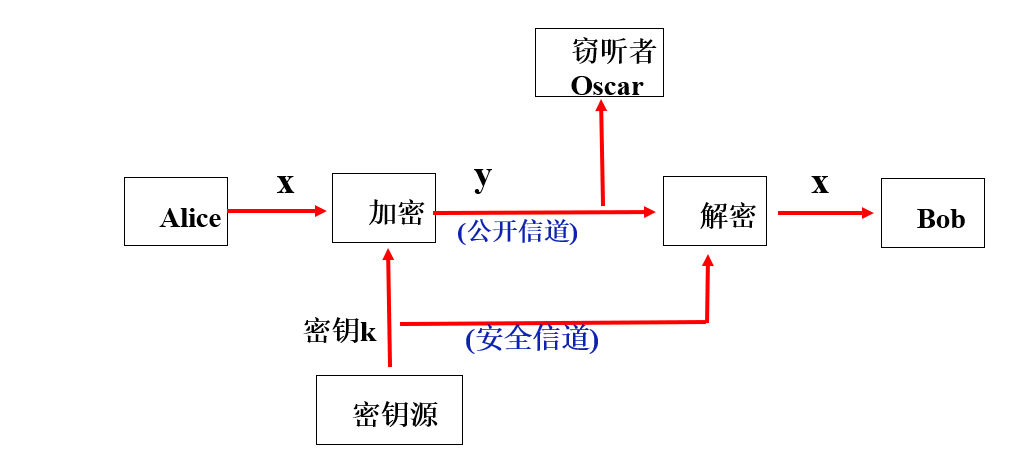
2. 密码系统定义

• 一个密码系统是一个五元组(P,C,K,E,D),
  • P:明文集
  • C:密文集
  • K:密钥集
  • E:加密算法集
  • D:解密算法集
• 密码学 Cryptography
• 加密 Encryption
• 解密 Decryption

置换密码

• 置换密码是根据一定的规划重新排列明文，以便打破明文的结构特征，也称为换位密码。
• 常见有两种：
  • 列置换密码
  • 周期置换密码

1.置换定义
在限集X上的运算：X->X若是双射函数，则称其为一个置换。

M=(1 2 3 4 5 6 7 8
   2 5 3 6 1 8 4 7)=(1 2 5)(3)(4 6  8 7)

逆置换

M^-1=(1 2 3 4 5 6 7 8
      2 5 3 6 1 8 4 7)^-1=(2 5 3 6 1 8 4 7
                           1 2 3 4 5 6 7 8)
     =(1 2 3 4 5 6 7 8
       5 1 3 7 2 4 8 6)=(1 5 2)(3)(4 7 8 6)

2.置换密码

• 加密：
• 解密：
• 攻击：
  • 穷举密钥进行攻击知道有意义的明文为止

3.周期置换密码

• 周期置换密码是将明文串P按照固定长度m分组，然后对每一组按照1,2,……,m的某个置换重新排列位置，从而得到密文C。
• 解密时将密文按照长度m分组，对每组按照逆置换重新排列，从而得到明文m。
  • 明文M=abcdefg,分组长度m=4,密钥=(1 3)(2 4)则密文C=cdabghef

m=(1 2 3 4
   3 4 1 2)
m1=(a b c d)->(c d a b)
m2=(e f g h)->(g h e f)
C=(cdabghef)

4.列置换密码

• 加密：
  • 将明文P以固定分组宽度m按行写出，每行m个字符，不足部分用空格代替，设有n行，得n行m列字符矩阵M;
  • 按1,2,……,m的某个位置交换列的位置次序，得字符矩阵M';
  • 将M'按1,2,……,m列的顺序依次独处密文序列C;

P=abcdefgh,分组宽为m=4,得2行4列矩阵M:
M=(a b c d
   e f g h)
设置换x=(1 3)(2 4)
则M'=(c d a b
      g h e f)
则密文序列C=cgdhaebf

解密：

• 将密文C以分组宽度m按照写出字符矩阵，的n行m列M';
• 按1,2,……,m的逆置换交换列的位置次序，得字符矩阵M;
• 将M按行的顺序依次独处明文序列P。

密文序列C=cgdhaebf
M'=(c d a b 
    g h e f)
逆置换x'=(1 3)(2 4)
M=(a b c d
   e f g h)

注：

1. 置换摩玛、周期置换密码、列置换密码三种加密方法本质上相同;
2. 三种加密方法都可以通过穷举密钥来进行攻击
3. 明文字母打乱后变成密文字母，字母相同不变，由密文中特殊的字母组成由意义的单词可去推测密钥的部分信息。