深度滤波器(1)——三角化得到深度值

为了详细了解单目稠密重建的细节，我们将会分几个专题来探讨深度滤波器的一系列内容。

1.三角化

2.三角化深度值的误差分析

3.深度滤波器的原理及实现

4.单目稠密重建的流程

---

 

本系列内容主要参考高翔《视觉SLAM十四讲》，这里加上自己的理解，做一个总结。

本篇博客我们来聊一聊三角化恢复深度信息。

目录：

(1)三角化的提出

(2)三角化公式

(3)求解深度的另外两种方法

附录

---

 

(1)三角化的提出

三角化最早由高斯提出，并应用于测量学中。简单来讲就是：在不同的位置观测同一个三维点P(x, y, z)，已知在不同位置处观察到的三维点的二维投影点X₁(x₁, y₁), X₂(x₂, y₂)_，利用三角关系，恢复出三维点的深度信息z。

(2)三角化公式

按照对极几何中的定义，设x₁, x₂为两个特征点的归一化坐标，则它们满足：

s₁x₁ = s₂Rx₂ + t                                                                公式(1)

=> s₁x₁ - s₂Rx₂ = t                                                            公式(2)

对公式(2)左右两侧分别乘以x_1^T，得：

s₁x₁^Tx₁ - s₂x₁^TRx₂ = x₁^T t                                                  公式(3)

对公式(2)左右两侧分别乘以(Rx₂)^_T，得：

s₁(Rx₂)^Tx₁ - s₂(Rx₂)^TRx₂ = (Rx₂)^T t                                     公式(4)

由公式(3)和公式(4)可以联立得到一个一元二次线性方程组，然后可以利用Cramer's法则（参见线性代数书）进行求解。

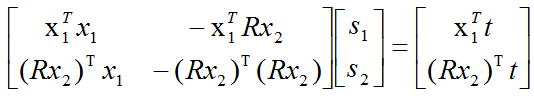
如下是对应的代码（如果大家感觉不易读懂，可以先跳过这段代码，等看完理论部分再返回来看不迟）

 1     // 方程
 2     // d_ref * f_ref = d_cur * ( R_RC * f_cur ) + t_RC
 3     // => [ f_ref^T f_ref, -f_ref^T f_cur ] [d_ref] = [f_ref^T t]
 4     //    [ f_cur^T f_ref, -f_cur^T f_cur ] [d_cur] = [f_cur^T t]
 5     // 二阶方程用克莱默法则求解并解之
 6     Vector3d t = T_R_C.translation();
 7     Vector3d f2 = T_R_C.rotation_matrix() * f_curr; 
 8     Vector2d b = Vector2d ( t.dot ( f_ref ), t.dot ( f2 ) );
 9     double A[4];
10     A[0] = f_ref.dot ( f_ref );
11     A[2] = f_ref.dot ( f2 );
12     A[1] = -A[2];
13     A[3] = - f2.dot ( f2 );
14     double d = A[0]*A[3]-A[1]*A[2];
15     Vector2d lambdavec = 
16         Vector2d (  A[3] * b ( 0,0 ) - A[1] * b ( 1,0 ),
17                     -A[2] * b ( 0,0 ) + A[0] * b ( 1,0 )) /d;
18     Vector3d xm = lambdavec ( 0,0 ) * f_ref;
19     Vector3d xn = t + lambdavec ( 1,0 ) * f2;
20     Vector3d d_esti = ( xm+xn ) / 2.0;  // 三角化算得的深度向量
21     double depth_estimation = d_esti.norm();   // 深度值

 

(3)求解深度的另外两种方法

a.利用叉乘进行消元进行求解

由

s₁x₁ = s₂Rx₂ + t                                                                公式(1)

左右两边同时乘以x₁的反对称矩阵，可得：

s₁x_1^{^}x₁ = 0 = s₂x_1^{^}Rx₂ + x_1^{^}t                                           公式(2)

由上式可解得s₂，

将s₂代入公式(1)，可求得s₁

 

b.利用Mid Point Method进行求解(Hartley大名鼎鼎的《Multiple View Geometry》中有讲解)

从此图中我们可以知道，理想情况下O₁P和O₂P会相交于空间中的一点，但是由于图像分辨率以及噪声的存在，实际的情况更可能是上图所描述的那样：O₁P和O₂P在空间中没有交点，这时我们需要找到一个O₁P与O₂P之间的公垂线，然后取其上的中点作为我们重建出的三维点，此即为Mid Point Method，具体的推导及公式请参看Hartley的《Multiple View Geometry》。

 

好了，今天的三角化深度信息我们就讲解到这里，下次课我们接着讨论三角化深度信息中的误差分析。

 

附录：

1.Cramer's 法则：

如果A的行列式不为0， Ax=b可以通过如下行列式进行求解：

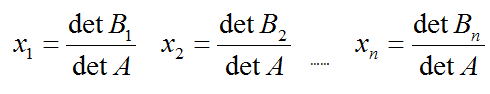
 矩阵B_j为A的第j列被b替换后得到的新的矩阵。

---

 

参考文献：

1.《视觉SLAM十四讲：从理论到实践》，电子工业出版社，2017，高翔等著。