树(二叉树)
树的概念
树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点, 所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结 构中有一个结点具有特殊的地位,这个结点称为该树的根结点,或简称为树根。
树(tree)是 n(n ≥ 0)个结点的有限集。
- 或者是一棵空树(n = 0),空树中不包含任何结点。
- 或者是一棵非空树(n > 0),此时有且仅有一个特定的称为根(root)的结点; 当n > 1 时,其余结点可分为m(m > 0)个互不相交的有限集T1,T2,…,Tm, 其中每一个本身又是一棵树,并且称为根的子树(sub tree)。
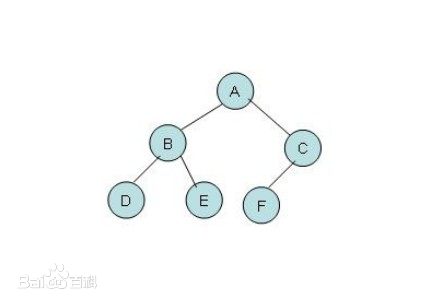
结点的层次(level):从0开始,如上图的层数是2;
兄弟(sibling):有同一个父节点的,如上E和F是兄弟,但是E和G不是兄弟节点。
数的深度(depth)或高度:最大层次数称为树的深度。如上:深度为2
结点的度(degree):拥有子树的数目称之为节点的度。如上:A和D的度是3;
二叉树
每个结点的度不超过2;并且每个孩子还有左孩子和有孩子之分。
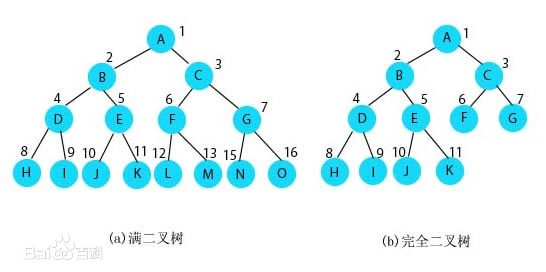
完全二叉树:在一棵满二叉树中,在最下层从最右侧起去掉相邻的若干叶子结点,得 到的二叉树即为完全二叉树。
满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树。
二叉树的存储方式
顺序结构
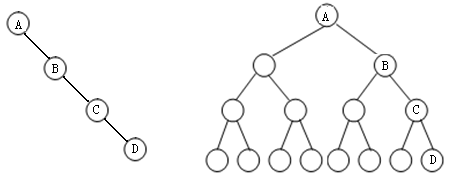
二叉树的顺序存储,就是用一组连续的存储单元存放二叉树中的结点。因此,必须把二叉树的所有结点安排成为一个恰当的序列,结点在这个序列中的相互位置能反映出结点之间的逻辑关系,用编号的方法从树根起,自上层至下层,每层自左至右地给所有结点编号,缺点是有可能对存储空间造成极大的浪费,在最坏的情况下,一个深度为k且只有k个结点的右单支树需要2k-1个结点存储空间。依据二叉树的性质,完全二叉树和满二叉树采用顺序存储比较合适,树中结点的序号可以唯一地反映出结点之间的逻辑关系,这样既能够最大可能地节省存储空间,又可以利用数组元素的下标值确定结点在二叉树中的位置,以及结点之间的关系。图5-5(a)是一棵完全二叉树,图5-5(b)给出的图5-5(a)所示的完全二叉树的顺序存储结构。

(a) 一棵完全二叉树 (b) 顺序存储结构
最坏的情况下:
链式存储结构
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。
通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。其结点结构为:
其中,data域存放某结点的数据信息;lchild与rchild分别存放指向左孩子和右孩子的指针,当左孩子或右孩子不存在时,相应指针域值为空(用符号∧或NULL表示)。利用这样的结点结构表示的二叉树的链式存储结构被称为二叉链表,如图5-8所示。
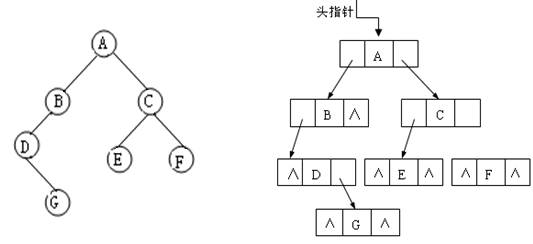
(a) 一棵二叉树 (b) 二叉链表存储结构
图5-8 二叉树的二叉链表表示示意图
二叉树的遍历
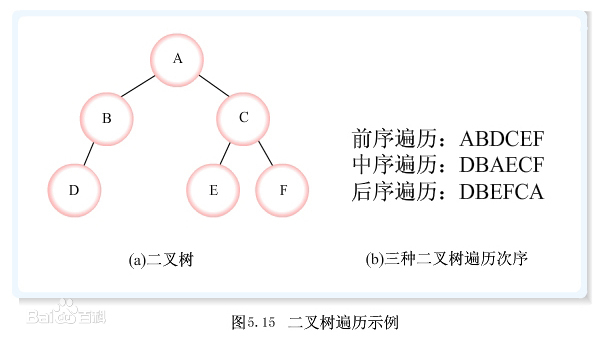
⑴ 先序遍历(DLR)二叉树的操作定义为: 若二叉树为空,则空操作;否则
① 访问根结点;
② 先序遍历左子树;
③ 先序遍历右子树。
⑵ 中序遍历(LDR)二叉树的操作定义为: 若二叉树为空,则空操作;否则
① 中序遍历左子树;
② 访问根结点;
③ 中序遍历右子树。
⑶ 后序遍历(LRD)二叉树的操作定义为: 若二叉树为空,则空操作;否则
① 后序遍历左子树;
② 后序遍历右子树;
③ 访问根结点。


