解决面试题的思路--5

　　前言：很多面试题都很抽象，不是很容易找到解决的办法。画图可以帮助自己去分析、推理面试题。下面用几个例题进行举例。

　　面试题19：

　　

　　镜像对于很多人来说是一个新的概念，未必一下子能想出来树的镜像；于是可以自己画一下，代码如下：

　　

#include<iostream>
#include<cstdlib>
using namespace std;

struct BinaryTreeNode
{
    int data;                                                    //节点数据
    BinaryTreeNode *lchild,*rchild;        //左孩子、右孩子
};
typedef struct BinaryTreeNode tree_t;

/******
    构造一个二叉树 递归实现
    参数：形参1：开始值，形参2：结束值
 ******/
tree_t *CreateTree(int i, int max) 
{
    //递归结束条件
    if(i > max)
    {
        return NULL;  //  == return 0;
    }
    
    tree_t *T;

    T = (tree_t *)malloc(sizeof(tree_t));    

    T->data = i;
    T->lchild = CreateTree(2*i, max); 
    T->rchild = CreateTree(2*i+1, max);
    return T;
}

//先序遍历输出二叉树
void FirstRoot_DLR(tree_t *p)
{
    if(p == NULL)
        return ;
    cout << " " << p->data;    
    FirstRoot_DLR(p->lchild);
    FirstRoot_DLR(p->rchild);
}

//中序遍历输出二叉树 程序中未使用
void MiddleRoot_DLR(tree_t *p)
{
    if(p == NULL)
        return;
    
    MiddleRoot_DLR(p->lchild);
    cout << " " << p->data;    
    MiddleRoot_DLR(p->rchild);
}

//后序遍历输出二叉树 程序中未使用
void LastRoot_DLR(tree_t *p)
{
    if(p == NULL)
        return;
    
    LastRoot_DLR(p->lchild);    
    LastRoot_DLR(p->rchild);
    cout << " " << p->data;
}

void MirrorRecursively(tree_t *pNode)
{
    if((pNode==NULL) || (pNode->lchild==NULL&&pNode->rchild==NULL))
        return;

    tree_t *pTemp = pNode->lchild;
    pNode->lchild = pNode->rchild;
    pNode->rchild = pTemp;

    if(pNode->lchild)
        MirrorRecursively(pNode->lchild);
        
    if(pNode->rchild)
        MirrorRecursively(pNode->rchild);
}

int main()
{
    tree_t *T1 = CreateTree(1,3);
    FirstRoot_DLR(T1);
    cout << endl;
    MirrorRecursively(T1);    
    FirstRoot_DLR(T1);
    cout << endl; 
    
    return 0;
}

　　面试题20：

　　题目如下：

　　

　　代码如下：

　　

#include<iostream>
using namespace std;

void printNum(int num)
{
    cout << " " << num;
}

void PrintMatrixInCircle(int (*numbers)[4],int col,int row,int start)
{
    int endX = col-1-start;
    int endY = row-1-start;

    //从左到右打印一行
    for(int i=start;i<endX;++i)
    {
        int num = numbers[start][i];
        printNum(num);
    }
    //从上到下打印一行
    if(start < endY)
    {
        for(int i=start+1;i<=endY;++i)
        {
            int num = numbers[i][endX];
            printNum(num);
        }
    }
    //从右到左打印一行
    if(start<endX && start<endY)
    {
        for(int i=endX-1;i>=start;--i)
        {
            int num = numbers[endY][i];
            printNum(num);
        }
    }
    //从下到上打印一行
    if(start<endX && start<endY-1)
    {
        for(int i=endY-1;i>=start+1;--i)
        {
            int num = numbers[i][start];
            printNum(num);
        }
    }
}

void PrintMatrixClockwisely(int (*numbers)[4],int col,int row)
{
    
    if(numbers==NULL || col<=0 || row<=0)
        return;

    int start = 0;
    

    while(col>start*2 && row>start*2)
    {
        PrintMatrixInCircle(numbers,col,row,start);
        ++start;
    }
    
}

int main()
{
    int num[4][4]={{1,2,3,4},{5,6,7,8},{9,10,11,12},{13,14,15,16}};
    
    PrintMatrixClockwisely(num,4,4);
    cout << endl;
    
    return 0;
}

　　面试题21：

　　面试题如下：

　　

　　分析:对于时间复杂度O(1)的实现，主要使用两个栈来实现的，代码如下：

　　

#include<stack>
#include<assert.h>
#include<iostream>
#include<vector>
#include<cstdlib>
#include<string>
#include<stdexcept>
using namespace std;

//模板类
template <typename T>
class StackWithMin{
    private:
        stack<int> m_data;    //数据栈
        stack<int> m_min;     //辅助栈
    public:
        void push(const T&);
        void pop();
        T min() const;
};

template <typename T> void StackWithMin<T>::push(const T& value)
{
    m_data.push(value);

    if(m_min.size()==0 || value<m_min.top())
        m_min.push(value);
    else
        m_min.push(m_min.top());
}

template <typename T> void StackWithMin<T>::pop()
{
    assert(m_data.size()>0 && m_min.size()>0);

    m_data.pop();
    m_min.pop();
}

template <typename T> T StackWithMin<T>::min() const
{
    assert(m_data.size()>0 && m_min.size()>0);

    return m_min.top();
}

int main()
{
    StackWithMin<int> intStack;
    
    //压入栈
    intStack.push(2);
    intStack.push(6);
    intStack.push(1);
    intStack.push(0);
    intStack.push(9);
    //弹出栈
    intStack.pop();
    
    //取最小值
    cout << "min: " << intStack.min() << endl;

    return 0;
}

　　面试题23：

　　面试题如下：

　　

　　分析：考察对二叉树和队列的理解，灵活运用数据结构的特点进行码代码，代码如下：

　　

#include<iostream>
#include<cstdlib>
#include<deque>
using namespace std;

struct BinaryTreeNode
{
    int data;                                                    //节点数据
    BinaryTreeNode *lchild,*rchild;        //左孩子、右孩子
};
typedef struct BinaryTreeNode tree_t;

/******
    构造一个二叉树 递归实现
    参数：形参1：开始值，形参2：结束值
 ******/
tree_t *CreateTree(int i, int max) 
{
    //递归结束条件
    if(i > max)
    {
        return NULL;  //  == return 0;
    }
    
    tree_t *T;

    T = (tree_t *)malloc(sizeof(tree_t));    

    T->data = i;
    T->lchild = CreateTree(2*i, max); 
    T->rchild = CreateTree(2*i+1, max);
    return T;
}

//先序遍历输出二叉树
void FirstRoot_DLR(tree_t *p)
{
    if(p == NULL)
        return ;
    cout << " " << p->data;    
    FirstRoot_DLR(p->lchild);
    FirstRoot_DLR(p->rchild);
}

//中序遍历输出二叉树 程序中未使用
void MiddleRoot_DLR(tree_t *p)
{
    if(p == NULL)
        return;
    
    MiddleRoot_DLR(p->lchild);
    cout << " " << p->data;    
    MiddleRoot_DLR(p->rchild);
}

//后序遍历输出二叉树 程序中未使用
void LastRoot_DLR(tree_t *p)
{
    if(p == NULL)
        return;
    
    LastRoot_DLR(p->lchild);    
    LastRoot_DLR(p->rchild);
    cout << " " << p->data;
}

//STL自带的deque(两端都可以进出的队列)
void PrintFromTopToBottom(tree_t *pTreeRoot)
{
    if(!pTreeRoot)
        return;

    deque<tree_t *> dequeTreeNode;
    dequeTreeNode.push_back(pTreeRoot);

    while(dequeTreeNode.size())
    {
        tree_t *pNode = dequeTreeNode.front();
        dequeTreeNode.pop_front();

        cout << " " << pNode->data;

        if(pNode->lchild)
            dequeTreeNode.push_back(pNode->lchild);
        if(pNode->rchild)
            dequeTreeNode.push_back(pNode->rchild);
    }
}

int main()
{
    tree_t *T1 = CreateTree(1,5);
    FirstRoot_DLR(T1);
    cout << endl;
    PrintFromTopToBottom(T1);
    cout << endl;    
    
    return 0;
}

　　面试题24：

　　　　

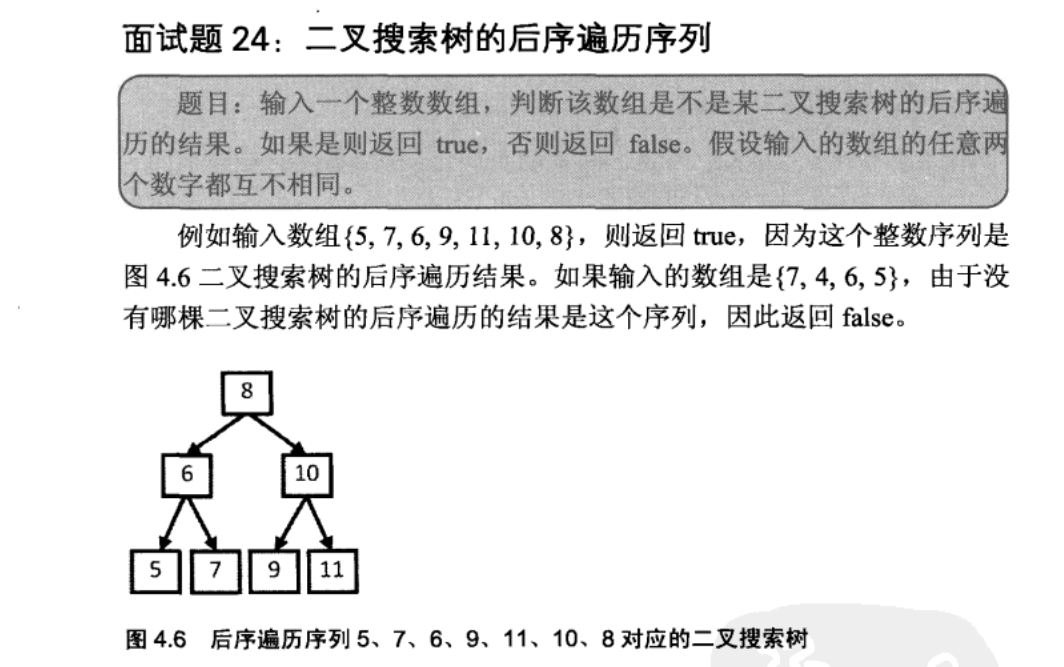
　　先简单介绍一下题目中的二叉搜索树的特点：左子树总比根节点小，右子树总比根节点大。代码如下：

　　

#include<iostream>
#include<cstdlib>
#include<deque>
using namespace std;

struct BinaryTreeNode
{
    int data;                                                    //节点数据
    BinaryTreeNode *lchild,*rchild;        //左孩子、右孩子
};
typedef struct BinaryTreeNode tree_t;

bool VerifySquenceOfBST(int data[],int len)
{
    if(data==NULL || len<=0)
        return false;

    int root = data[len-1];

    //二叉搜索树的左子树节点小于根节点
    int i = 0;
    for(;i<len-1;++i)
    {
        if(data[i] > root)
            break;
    }
    //二叉搜索树的右子树大于根节点
    int j = i;
    for(;j<len-1;++j)
    {
        if(data[j] < root)
            return false;
    }
    //判断左子树是不是二叉搜索树
    bool left = true;
    if(i > 0)
        VerifySquenceOfBST(data,i);

    //判断右子树是不是二叉搜索树
    bool right = true;
    if(j > 0)
        VerifySquenceOfBST(data,j);

    return (left && right);
}

int main()
{
    int data[]={5,7,6,9,11,10,8};
    cout << boolalpha << VerifySquenceOfBST(data,7) << endl;    
    
    return 0;
}

　　面试题15：

　　面试题如下：

　　

　　代码如下：

　　

#include<iostream>
#include<cstdlib>
#include<deque>
#include<stdio.h>
#include<vector>
using namespace std;

struct BinaryTreeNode
{
    int data;                                                    //节点数据
    BinaryTreeNode *lchild,*rchild;        //左孩子、右孩子
};
typedef struct BinaryTreeNode tree_t;

/******
    构造一个二叉树 递归实现
    参数：形参1：开始值，形参2：结束值
 ******/
tree_t *CreateTree(int i, int max) 
{
    //递归结束条件
    if(i > max)
    {
        return NULL;  //  == return 0;
    }
    
    tree_t *T;

    T = (tree_t *)malloc(sizeof(tree_t));    

    T->data = i;
    T->lchild = CreateTree(2*i, max); 
    T->rchild = CreateTree(2*i+1, max);
    return T;
}

//先序遍历输出二叉树
void FirstRoot_DLR(tree_t *p)
{
    if(p == NULL)
        return ;
    cout << " " << p->data;    
    FirstRoot_DLR(p->lchild);
    FirstRoot_DLR(p->rchild);
}

//中序遍历输出二叉树 程序中未使用
void MiddleRoot_DLR(tree_t *p)
{
    if(p == NULL)
        return;
    
    MiddleRoot_DLR(p->lchild);
    cout << " " << p->data;    
    MiddleRoot_DLR(p->rchild);
}

//后序遍历输出二叉树 程序中未使用
void LastRoot_DLR(tree_t *p)
{
    if(p == NULL)
        return;
    
    LastRoot_DLR(p->lchild);    
    LastRoot_DLR(p->rchild);
    cout << " " << p->data;
}

void FindPath(tree_t *pRoot,int num,vector<int> &path,int &cursum)
{
    cursum += pRoot->data;
    path.push_back(pRoot->data);

    //如果是根节点，并且路径上的和等于输入的值
    //打印出这条路径
    bool isLeaf = pRoot->lchild==NULL && pRoot->rchild==NULL;
    if(cursum==num && isLeaf)
    {
        cout << "A path is found: ";
        vector<int>::iterator iter = path.begin();
        for(;iter!=path.end();++iter)
            printf("%d\t",*iter);

        printf("\n");
    }

    //如果不是叶节点，则遍历子节点
    if(pRoot->lchild != NULL)
        FindPath(pRoot->lchild,num,path,cursum);
    if(pRoot->rchild != NULL)
        FindPath(pRoot->rchild,num,path,cursum);

    //再返回子节点之前,在路径上删除当前节点
    //并在cursum中减去当前节点的值
    cursum -= pRoot->data;
    path.pop_back();
}

void FindPath(tree_t *pRoot,int num)
{
    if(pRoot == NULL)
        return;

    vector<int> path;
    int cursum = 0;
    FindPath(pRoot,num,path,cursum);
}

int main()
{
    tree_t *T1 = CreateTree(1,5);
    FirstRoot_DLR(T1);
    cout << endl;
    FindPath(T1,8);
    
    return 0;
}

　　总结：主要培养一种思想，通过举例的方法让抽象问题变为具体化。