后缀自动机

WX 讲的太抽象了，不想听。

定义

• 给定一张 DAG，边有边权。称节点为状态，边为转移。

• 有源点 \(t_0\) 称其为初始状态，有至少一个汇点满足从 \(t_0\) 走到这个节点经过的边组成的字符串是 \(S\) 串的后缀。

• 所有的从 \(t_0\) 出发的路径都可以找到对应的 \(S\) 中的字串（连续的），每一个 \(S\) 中的字串都有一个从 \(t_0\) 出发的路径与之对应。

如果满足上面的条件，而且节点是最少的那么这个图就是一个后缀自动机。

\(\text{endpos}\)

定义 \(\text{endpos}(t)\) 表示字符串 \(t\) 出现在 \(S\) 的字串中最后一个元素的位置，需要注意 \(t\) 可能在 \(S\) 中多次出现，所以 \(\text{endpos}(t)\) 是一个集合。

举个例子，\(S=\texttt{dczzcz}\)，\(t=\texttt{cz}\)，那么就有 \(\text{endpos}(t)=\{3,6\}\)。

等价类

如果两个字符串 \(t_1\) 和 \(t_2\) 满足 \(\text{endpos}(t_1)=\text{endpos}(t2)\) 那么就称 \(t_1\) 和 \(t_2\) 在一个等价类中。注意必须要是相等，而包含关系不算。

等价类有一些性质：

1. 如果 \(t1,t2\) 属于一个等价类而且 \(\lvert t_1\rvert\lt \lvert t_2\rvert\)，那么 \(t_1\) 一定是 \(t_2\) 的字串。
2. 如果 \(\lvert t_1\rvert\lt \lvert t_2\rvert\)，那么一定有 \(\text{endpos}(t1)\cup\text{endpos}(t2)=\varnothing\) 或者 \(\text{endpos}(t1)\subseteq \text{endpos}(t2)\)。
3. 一个等价类里的字符串的长度是连续的。

性质容易证明，故不再赘述。

\(\text{len}\&\text{link}\)

对于 SAM 上的一个节点 \(v\)，定义 \(len(v)\) 表示从 \(t_0\) 到所经过的边的数量，换而言之也就是一这个点结尾的左右的子串中最长的一个的长度。

oi-wiki 上有一个显然：所有从 \(t_0\) 到达状态 \(v\) 经过的转移形成的字符串的 \(\text{endpos}\) 相等。

于是有一个强有力的性质，所有从 \(t_0\) 到达状态 \(v\) 经过的转移形成的字符串都属于一个等价类。

甚至这个性质的逆命题也是正确的，也就是所有等价类一样的字串的状态都是一样的。

oi-wiki 都不会证，好像要用 迈希尔－尼罗德定理 证明 SAM 是正则的。

考虑对于一个状态 \(v\)，定义 \(\text{link}(v)\) 表示这个等价类中最短的字符串删除了第一个字母之后做得到的字符串的等价类对应的状态。

为了便于陈述 \(\text{link}(v)\) 的性质，定义 \(\text{endpos}(t_0)=\mathbb{R}\)。

引理 1

把 \(\text{link}(v)\) 设置一条连向 \(v\) 的边，那么得到的图就一定是一个以 \(t_0\) 为根的外向的树。

证明：

因为 \(\text{link}\) 在求解的时候是通过不断删除字符计算的，所以对于任意一个状态一直令 \(v\gets\text{link}(v)\) 最终都会有 \(v=t_0\)。

因为每一个状态 \(v\) 都只有一个出边，而且最终汇入了 \(t_0\) 所以这样得到的把边反转的图一定是一棵树。

引理 2

考虑一种新的建树方式：

对于两个状态 \(u,v\)，如果 \(\text{endpos}(u)\subsetneqq \text{endpos}(v)\) 而且 \(\nexists x\mid \text{endpos}(u)\subsetneqq\text{endpos}(x)\subsetneqq\text{endpos}(v)\)，那么我们把 \(u\) 想 \(v\) 连接一条边。

有性质这样用 \(\text{endpos}\) 和 \(\text{link}\) 建出的树是一样的。

证明容易理解，结合前面的这个性质：

如果 \(\lvert t_1\rvert\lt \lvert t_2\rvert\)，那么一定有 \(\text{endpos}(t1)\cup\text{endpos}(t2)=\varnothing\) 或者 \(\text{endpos}(t1)\subseteq \text{endpos}(t2)\)。

操作

SAM 与 SA 不同，它是一个在线的算法，也就是我们可以在字符串 \(S\) 后面动态的添加字符然后更新 SAM。

流程

考虑令 \(t_0\) 的编号为 \(0\)，\(\text{link}(t_0)=-1\)，\(\text{len}(t_0)=0\)。

如果添加的新字符为 \(c\)，那么过程如下：

1. 令 \(lst\) 为添加 \(c\) 之前的 \(\text{len}\) 最大的状态，也就是例子的 \(10\) 节点（如果是第一步那么我们令 \(lst=0\)）。
2. 为了可以表示整个字符串，我们必定要新建一个节点 \(cur\)，显然 \(\text{len}(cur)=\text{len}(lst)+1\)。
3. 从 \(lst\) 开始，依次遍历 \(\text{link}(lst),\text{link}(\text{link}(lst)),\text{link}(\text{link}(\text{link}(lst))),\cdots\)，如果遍历到的节点不存在一条转移为 \(c\) 那么就新建一个为 \(c\) 的转移连接 \(cur\)。
4. 如果访问到了 \(t_0\)，那么就令 \(\text{link}(cur)=0\)，回到第一步。
5. 如果在访问时遇到了一个状态有为 \(ch\) 的转移，那么令这个状态为 \(p\)，这个转移到达的状态为 \(q\)。‘
6. 如果有 \(\text{len}(p)+1=\text{len}(q)\)，那么令 \(\text{link}(cur)=q\)，\(lst=cur\)，回到第一步。
7. 新建一个状态 \(op\)，把 \(q\) 的所有信息（包括 \(\text{link}\) 和所有的出边），\(\text{len}(op)=\text{len}(p)+1\)，令 \(\text{link}(q)=op,\text{link}(cur)=op\)。
8. 将 \(p\) 以及 \(p\) 的一堆父亲中，所有指向 \(q\) 的边指向 \(op\) 以替代。
9. 停止遍历，\(lst=cur\) 然后回到第一步。

正确性证明

考虑在一个字符串的末尾添加一个字符，那么显然这个字符可以与前面的所有的后缀连接在一起组成新的子串。

对于新产生的子串有两种可能：新出现的和没有出现的。

为了添加这些东西，显然我们需要遍历所有的后缀，也就是访问 \(\text{link}\) 因为 \(\text{link}\) 的定义就是在这个等价类中不断的删除最开始的字符得到的新等价类。

因为 \(c\) 的加入使原本的字符串新加入了位置，所以要想让原串加入一个 \(c\) 之后的 \(\text{endpos}\) 不一样只能是在前面的子串中出现了新串的后缀。

因为 \(\text{link}(cur)\) 的定义是 \(cur\) 所在的等价类中最短的元素删除头所得到，那么我们需要找到的就是新串的后缀在前面原串中作为子串出现的信息，因为只有这样 \(\text{endpos}\) 才会因为新元素的加入而改变。

显然根据 \(\text{link}\) 的定义，\(\text{link}(cur)\) 指向的应该是原串中与新串的后缀相同的最长的子串的等价类的对应的状态。

因为我们通过 \(\text{link}\) 访问到的等价类内最长的元素是所在等价类中最短的字符串删除头，所以显然 \(\text{link}\) 指向的等价类中最长的字串是现在的等价类中最短的子串的子串。

而因为在同一个等价类中，较短的字符串一定是较短字符串的子串，所以这个等价类中的所有字符串都是原串的后缀。

此时有两种情况，如果这个等价类没有转移为 \(c\)，那么就直接添加就行了，然后继续访问后缀。

如果现在访问到的等价类中有 \(c\) 的转移，那么就一个现在所在的等价类 \(p\) 的字符串在头添加了 \(c\) 之后到达的等价类的 \(q\) 中有的串有与后缀相同的部分。

接下来有两种情况，如果等价类 \(q\) 中最长的字符串都是新串的后缀，那么显然整个 \(q\) 的 \(\text{endpos}\) 都会因为新的加入而改变，直接把 \(\text{link}(cur)\) 设置为 \(q\) 就行了。

如果满足上面的情况，那么需要满足 \(p\) 的最长的字符串在末尾添加了 \(c\) 之后就是 \(q\) 这个等价类中所拥有的最长的字符串，也就是 \(\text{len}(p)+1=\text{len}(q)\)。

对于另一种情况，也就是等价类 \(q\) 中有一部分的字符串是新串的后缀而有一部分不是，所以就考虑把现在的等价类分割成为两个部分，一个部分是后缀而另外一个则不是。

把上面的操作放在 \(\text{endpos}\) 的视角看也就是有的 \(\text{endpos}\) 改变了而有的没有改变，把没有改变的字符串放在原处而新建出改变的等价类。

因为 \(\text{link}(cur)\) 所需要指向的是 \(\text{endpos}\) 真包含自己的 \(\text{endpos}\) 的最长的后缀所属于的等价类，所以限显然 \(\text{link}(cur)=op\) 也就是新建的节点。

因为我们取出的一部分字串就是满足等价类 \(p\) 中最长的字符串在末尾添加了字符 \(c\) 时候在 \(op\) 中最长，所以 \(\text{len}(op)=\text{len}(p)+1\)。

因为等价类 \(op\) 的 \(\text{endpos}\) 就是在等价类 \(q\) 的 \(\text{endpos}\) 的基础上新添加了一个位置，所以显然根据引理 \(2\) 可以得到 \(\text{link}(q)=op\)。

因为等价类中最有的字符串 \(op\) 是的一大堆祖先的等价类中的字串，也就是后缀所以所有的祖先的 \(\text{endpos}\) 都会增加一个位置，所以原本指向 \(q\) 的节点就都应该指向 \(op\) 了。

模拟

如果你还是不明白，那么就去模拟吧！

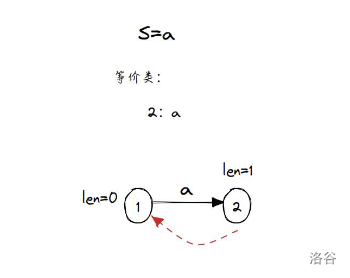
从上图到下图是第 \(1\) 种情况，\(p=0\) 直接结束了。

从上图到下图是第 \(1\) 种情况，不断通过红边相会一直走到 \(1\) 都没有遇到为 \(b\) 的出边。

从上图到下图是第 \(3\) 种情况，在访问到 \(1\) 的时候遇到了有为 \(b\) 的出边，它指向了 \(4\)。

这时 \(p=1,q=4\)，因为 \(0+1\ne 3\) 或者说 \(\text{len}(1)+1\ne \text{len}(3)\) 所以新建了 \(6\) 号节点 \(op\) 作为新的节点。

然后 \(6\) 号节点复制了 \(4\) 号节点的出边，然后把 \(4\) 号节点和 \(5\) 号节点的 \(\text{link}\) 设置为了 \(6\)。

从 \(6\) 开始访问通过红边访问，没有遇到指向 \(4\) 的值为 \(b\) 的边，所以不需要改变。

把 \(6\) 的红边设置为了 \(1\)，把 \(1\) 原本指向 \(4\) 的边改变到了 \(6\)。

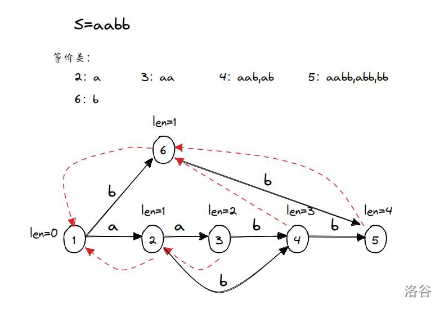
从上图到下图是第 \(2\) 种情况，在访问到 \(1\) 的时候遇到了一个为 \(a\) 的出边指向 \(2\)。

此时 \(p=1,q=2\)，因为 \(0+1=1\) 或者说 \(\text{len}(1)+1=\text{len}(2)\) 所以直接把 \(\text{link}\) 设置为 \(2\) 就可以了。

在下面再放两张图，可以自己模拟一下：

• https://cdn.luogu.com.cn/upload/image_hosting/5ag5mc15.png
• https://cdn.luogu.com.cn/upload/image_hosting/aqm2i07p.png

实现

考虑对于每一个节点，类似于字典树的开一个长度为 \(\lvert\sum\rvert\) 的数组记录出边。

对于遇到的操作，直接模拟即可。

struct NODE{int to[26],len,link;NODE(){memset(to,0,sizeof(to));len=0;}}sam[N<<1];
int las=1,tot=1,n;
char a[N];
void add(int c){
	int p=las;int np=las=++tot;sam[np].len=sam[p].len+1;
	for(;p&&!sam[p].to[c];p=sam[p].link) sam[p].to[c]=np;
	if(!p){sam[np].link=1;return;}
    int q=sam[p].to[c];
    if(sam[q].len==sam[p].len+1){sam[np].link=q;return;}
    int nq=++tot;sam[nq]=sam[q];
    sam[nq].len=sam[p].len+1,sam[q].link=sam[np].link=nq; 
    for(;p&&sam[p].to[c]==q;p=sam[p].link) sam[p].to[c]=nq;
}

时间复杂度分析

对于 SAM 的时间复杂度分析，我们都认为 \(\lvert\sum\rvert\) 对时间复杂度造成的影响为常数。

如果使用 map 存边那么时间复杂度为 \(O(n\log\lvert\sum\rvert)\)，空间复杂度为 \(O(n)\)。

如果使用直接开一个大小可以存储 \(\sum\) 中所有字符的数组存边，那么时间复杂度为 \(O(n)\)，空间复杂度为 \(O(n\lvert\sum\rvert)\)。

另外，请一定不要使用 unordered_map 因为可以用 SAM 解决的问题一般都要卡 unordered_map。

对于 SAM 的建立，有一些操作并不能明显的看出是线性的，考虑在下面分析一下。

但是在进行针对性的分析之前，我们需要先证明 SAM 的转状态和转移的个数都是线性的。

状态数

对于一个长度为 \(n(n\gt 1)\) 的字符串，其 SAM 的状态数不超过 \(2n-1\)。

其实这个算法的实现本身也可以证明这个结论，因为每一个操作我们都只会新建 \(2\) 个节点而且第 \(1\) 步和第 \(2\) 步都只会新增一个节点。

同时，因为 SAM 的每一个状态都对应这一个 \(\text{endpos}\)，所以我们在同时也证明了一个长度为 \(n\) 的字符串的等价类和不同的 \(\text{endpos}\) 不会超过 \(2(n-1)\) 个。

转移数

对于一个长度为 \(n(n\gt 2)\) 的字符串，其 SAM 的转移数不超过 \(3n-4\)。

证明：

对于这个上界，感性理解发现可以通过类似于 \(\texttt{abbbbb}\) 的字符串产生，因为这样每一次都会新建节点然后复制一遍。

容易发现这是的转移数量为 \(3n-4\)，至于陈立杰高级的证明方法我是完全没有看懂，个人认为过于的意识流了一点。

笔者打算去阅读一下国家集训队的论文，然后再回来填坑。

情况 1

对于从 \(las\) 开始向前遍历，为所有没有为 \(c\) 出边的节点添加出边。

证明：

因为 SAM 中最多有的状态数是 \(O(n)\) 的，而且每一个节点最多只会被添加一个为 \(c\) 的出边，所以为 \(c\) 的出边的个数必定是 \(O(n)\) 的。

因为遍历操作每访问一次都会加一个为 \(c\) 的出边，所以先让这个操作的时间复杂度为 \(O(n)\)。

情况 2

在 \(q\) 复制到 \(op\) 的过程。

证明：

因为复制的会使出边的数量增加，而 SAM 的出边的个数又是 \(O(n)\) 的，所以这个操作也是 \(O(n)\) 的。

情况 3

把 \(q\) 复制到 \(op\) 之后去遍历 \(p\) 的祖先。

证明：

我们定义一个等价类 \(p\) 的最长的字符串为 \(\text{longest}(p)\)，显然这是一个添加了 \(c\) 之后的字符串的后缀。

这是如果 \(p\) 所在的位置与 \(las\) 之间的 \(\text{link}\) 的数量大于 \(2\)，那么 \(p\) 将会被 \(cur\) 的 \(\text{link}\) 指向。

而容易理解这个位置是会不断递减的，换而言之 \(\text{longest}(\text{link}(\text{link}(las)))\) 的位置是单调的。

综上所述，这个循环不会被执行超过 \(O(n)\) 次。

应用

求解字串出现次数

容易理解对于一个等价类里的字串，其出现次数就是 \(\text{endpos}\) 的大小。

有一个误区，那就是如果有 \(\text{link}\) 连接，其实 \(\text{endpos}\) 的大小差距不一定是 \(1\)。

只有 \(cur\) 的 \(\text{link}\) 一定是，所以应该在 DP 的只把 \(\text{cur}\) 的大小记录成 \(1\)，转移的时候这个节点的大小就是其子节点的大小的和。

另外，一个等价类中最长的字符串的长度就是 \(\text{len}\)。

最小表示

把求解的字符串重复一遍，建立 SAM。

从源点开始贪心的走 \(n\) 步，最后得到的就是最小表示。

不同子串个数

容易想到，对于新添加的一个 \(cur\)，其贡献就是 \(\text{maxlen}(cur)-\text{minlen}(cur)+1\)，也就是 \(\text{len}(cur)-\text{len}(\text{link}(cur))\)。

之所以如果新添加一个点不计算贡献，是因为其贡献在上一次重复的时候已经计算过了，新加入点的本质是把以前出现的串分类。