Snow Walking Robot 的题解

题目大意

给你一个机器人和机器人的 \(n\) 个运动，要求你在给出的运动路径的基础上设计一种不会走重复的路径的方法，注意只能减少原来的步数而不能增加，其中 \(1\le n\le 10^5\)。

思路

因为这道题目可以自由的配置路径并且要求机器人在最后回到原来的位置，那么就应该要到一种适合所有的移动步数的方法。

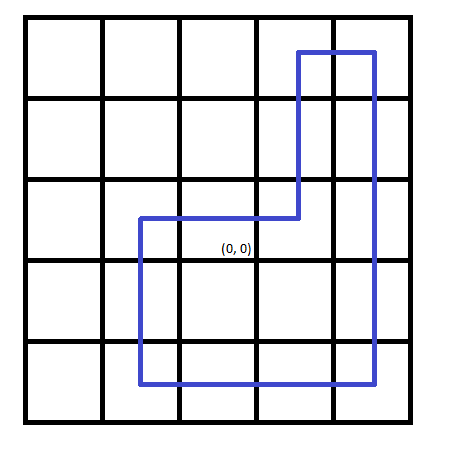
我们可以将所有的移动进行平移操作，把路径移动成下面这样。

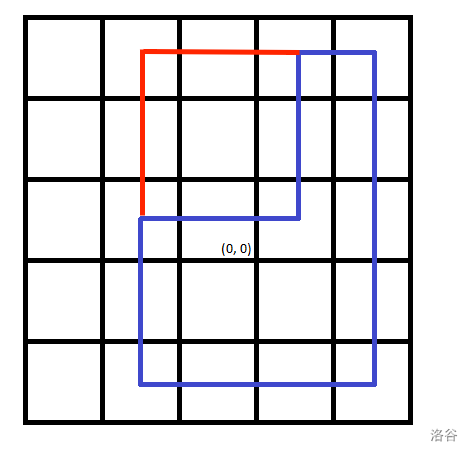
这样，对于所有的移动，在知道了步数之后，就可以用 \(O(4\times n)\) 的时间快速输出了，\(n\) 为边长。

因为题目给出的操作只能删除，而且要求回到最初的位置，所以向上、向下和向左、向右的数量应该就是一样的了，所以应该取最小值。

但是有一些特殊情况需要特判一下：当向上、向下或者向左、向右的数量有一个是 \(0\) 的时候并不是不可以的，要注意向左紧接着向右或者向上之后紧接着向下也是合法的。

AC Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,s[5];
char a[N];
void solve(){
	memset(s,0,sizeof(s));
	int ans=0;
	cin>>a+1,n=strlen(a+1);
	for(int i=1;i<=n;i++){
		if(a[i]=='R') s[1]++;
		if(a[i]=='D') s[2]++;
		if(a[i]=='L') s[3]++;
		if(a[i]=='U') s[4]++;
	}ans+=min(s[1],s[3])*2;
	ans+=min(s[2],s[4])*2;
	if(min(s[1],s[3])==0&&min(s[2],s[4])==0){puts("0\n");return;}
	if((min(s[1],s[3])==0)||(min(s[2],s[4])==0)){
		if(min(s[1],s[3])==0) cout<<"2\nDU\n";
		if(min(s[2],s[4])==0) cout<<"2\nLR\n";
		return;
	}
	cout<<ans<<endl;
	for(int i=1;i<=min(s[1],s[3]);i++) cout<<'R';
	for(int i=1;i<=min(s[2],s[4]);i++) cout<<'D';
	for(int i=1;i<=min(s[1],s[3]);i++) cout<<'L';
	for(int i=1;i<=min(s[2],s[4]);i++) cout<<'U';
	puts("");
	
}signed main(){
	int T;cin>>T;
	while(T--) solve();
	return 0;
}