CF1896E Permutation Sorting 的题解

题目描述

给定一个有 \(1\) 至 \(n\) 组成的排列 \(a_1,a_2,\cdots ,a_n\)。如果下标 \(i=a_i\)，则认为这个下标是好下标。现在每秒将不好的下标循环右移一位，求下标为 \(1\) 至 \(n\) 变为好下标的最早时刻。

思路

因为移动有环，所以将数组破环为链。

接着将对应点与目标点连线。

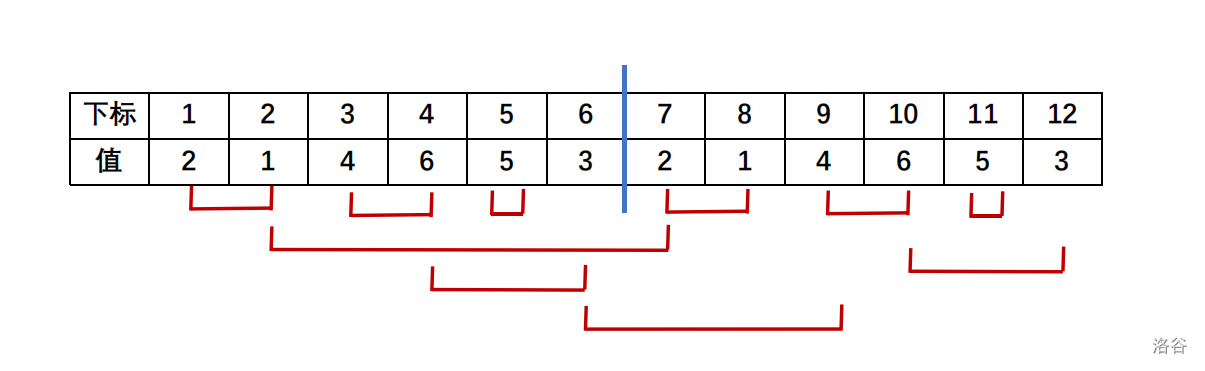
设 \(x\) 的最终移动位置为 \(s_x\)，那么在 \(x\to s_x\) 的过程中已经有 \(y \to s_y\) 到达了位置，那么 \(x\) 的移动次数就会减少 \(1\)，因为在 \(x\) 移动到 \(s_y\) 这个位置是就直接跳过了。注意，在连线的时候，不光要处理 \(s_x<n\) 的连线，序列复制的部分也要处理。因此，对于 \(x\) 移动到 \(s_x\)，就是 \(x\) 到 \(s_x\) 的距离减去 \(x\to s_x\) 之间包含的区间的个数。

所以题目就转化成为了求解 \(n\) 个区间内包含的区间数，即满足 \(x<y\) 且 \(s_x>s_y\) 的 \(y\) 数量，也就是一个二位偏序问题。所以将 \(x\) 作为下标，将 \(s_x\) 作为具体值放入树状数组中进行求解。

AC Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
#define lowbit(x) x&-x
const int N=2e6+6;
int n,a[N],s[N],l[N],r[N],x[N],ans[N];
void updata(int x){
	for(int i=x;i<=n*2;i+=lowbit(i)) s[i]++;
}int sum(int x){
	int ans=0;
	for(int i=x;i>=1;i-=lowbit(i)) ans+=s[i];
	return ans;
}
void solve(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++){
		l[i]=i;
		if(a[i]<i) r[i]=a[i]+n,r[i+n]=2e6;
		else r[i]=a[i],r[i+n]=a[i]+n;
	}//for(int i=2*n;i>=1;i--) cout<<r[i]<<" ";cout<<endl;
	for(int i=n*2;i>=1;i--){
		//cout<<sum(x[i])<<" ";
		//cout<<r[i]<<" "<<i<<endl;
		if(i<=n) ans[a[i]]=r[i]-l[i]-sum(r[i]);
		//cout<<sum(r[i])<<" "<<r[i]<<endl;
		updata(r[i]);
	}for(int i=1;i<=n;i++) cout<<ans[i]<<" ";cout<<endl;
	for(int i=1;i<=n*2;i++) a[i]=s[i]=l[i]=x[i]=ans[i]=0;
}signed main(){
	int T;cin>>T;
	while(T--) solve();
	return 0;
}