群论学习笔记
群的定义
给定一个集合 \(G=\{a,b,c\cdots\}\) 和集合上的二元运算 "\(*\)",如果满足以下条件:
(1)封闭性。对于任意的 \(a,b \in G,a*b\in G\) 成立。
(2)结合律。对于任意 \(a,b,c \in G,a*(b*c)=(a*b)*c\) 成立。
(3)存在单位元。 \(G\) 中存在一个元素 \(e\),使得对于 \(G\) 中任意元素 \(a\) ,都有 \(a*e=e*a=a\),元素 \(e\) 为单位元素。
(4)存在逆元。对于 \(G\) 中任意元素 \(a\),恒有一个 \(b \in G\) ,使得 \(a*b=b*a=e\),则元素 \(b\) 为元素 \(a\) 的逆元,记作 \(a^{-1}\)。
则称集合 \(G\) 是运算 "\(*\)" 下的一个群
置换群
置换,就是给我们一个 \(n\) 个数的排列 $1 , 2 ,\cdots n $ ,我们通过置换得到 \(1 \sim n\) 的映射 \(p_1,p_2,p_3\cdots p_n\)
它们一一对应:\(\binom{1\ 2\ 3\ ...n}{p_{1}\ p_{2} \ p_{3} ...p_{n}}\)
置换实际上就表示为元素位置的变化
集合 \(S\)上的所有置换关于置换的乘法满足封闭性、结合律、有单位元(恒等置换,即每个元素映射成它自己)、有逆元(交换置换表示中的上下两行),因此构成一个群
这个群的任意一个子群即称为置换群
有一种特殊的置换叫做循环置换
把 \(m\) 阶循环记为 \(\binom{a_{1}\ a_{2} ...\ a_{m-1} \ a_{m}}{a_{2}\ a_{3} ...\ a_{m} \ a_{1}}\)
特别的,当 \(m=2\) 时,\(2\) 阶循环 \((i,j)\) 叫做 \(i\) 和 \(j\) 的对换或换位
Burnside引理
定义 \(G\) 为一个置换群,定义其作用于 \(X\),如果 \(x,y\in X\) 在 \(G\)作用下可以相等即存在 \(f\in G\) 使得 \(f(x)=y\) 则定义 \(x,y\) 属于一个等价类,则不同的等价类的数量为:
\(|X/G|=\dfrac{1}{|G|}\sum_{g\in G} X^g\)
其中, \(X^g\) 为 \(X\) 在 \(g\) 作用下的不动点的数量,即满足 \(g(x)=x\)
简单来说,就是每个置换的不动点的个数的平均值就是不同的方案数
举一个例子
如图所示,\(2×2\) 方格中每个格子可以选择染上\(2\) 种颜色(红色或白色),那么总共是 \(2^4=16\) 种情况
现在要问,如不旋转、顺时针旋转 \(90\) 度、逆时针旋转 \(90\) 度、旋转 \(180\) 度后相同的均算成同一种方案,问总共有多少种不同的方案
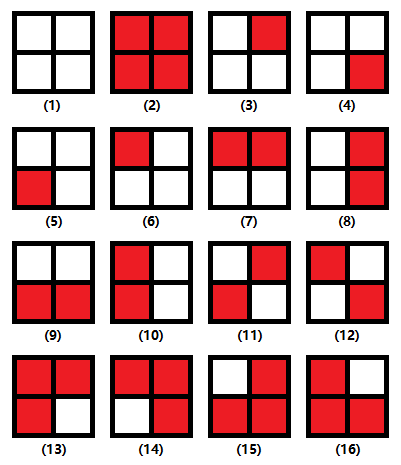
可以把四种操作分别看成四种置换
分别统计这四种置换下不动点的个数
\(1\)、不旋转,所有的元素均为不动点,一共有 \(16\) 个
\(2\)、顺时针旋转 \(90\) 度,不动点有 \(1,2\)
\(3\)、逆时针旋转 \(90\) 度,不动点有 \(1,2\)
\(4\)、旋转 \(180\) 度,不动点有 \(1,2,11,12\)
答案为 \(\frac{16+2+2+4}{4}=6\)
Polya 定理
对于每一种置换,我们一定可以把它表示为循环的形式
定义循环的循环节为循环的个数
设 \(k\) 为颜色种类,\(m(f)\) 为置换 \(f\) 的循环节
在置换群中,等价类个数(方案数)等于所有置换 \(f\) 的 \(k^{m(f)}\) 的平均数,即
\(\dfrac{1}{|G|}\sum_{g\in G}m^{c(g)}\)
对于每一个循环,如果想让这个循环中有不动点,那么这个循环中所有元素的颜色应该是相同的
而不同的循环之间是没有影响的,所以一个循环的答案就是 \(m^{c(g)}\)
同样是上面的例子

\(1、\)不旋转,\(f_1 = \binom{1234}{1234} = (1)(2)(3)(4), C(f) = k ^ {m(f)} = 2 ^ 4 = 16\)
\(2\)、顺时针旋转 \(90\) 度,\(f_2 = \binom{1234}{2341} = (1,2,3,4), C(f) = k ^ {m(f)} = 2 ^ 1 = 2\)
\(3\)、逆时针旋转 \(90\) 度,\(f_1 = \binom{1234}{4123} = (1,2,3,4), C(f) = k ^ {m(f)} = 2 ^ 1 = 2\)
\(4\)、旋转 \(180\) 度,\(f_1 = \binom{1234}{3412} = (1,3)(2,4), C(f) = k ^ {m(f)} = 2 ^ 2 = 4\)
答案为 \(\frac{16+2+2+4}{4}=6\)
例题
P4980 【模板】Pólya 定理
这道题中一共有 \(n\) 种不同的置换,分别是整体平移 \(1 \sim n\) 个单位
假设平移了 \(i\) 个单位,那么要平移 \(lcm(i,n)\) 步才能回到起点
那么循环节为 \(\frac{in}{lcm(i,n)}=gcd(i,n)\)
就可以直接套用 \(polya\) 定理
\(ans=\frac{1}{n}\sum\limits_{i=1}^n n^{gcd(i,n)}\)
进行一下莫比乌斯反演,答案就为 \(\sum\limits_{d|n}n^d\varphi(n/d)\)
P1446 [HNOI2008]Cards
因为有使用颜色的限制所以不能直接套用 \(polya\) 引理
而要枚举每一种置换下不动点的个数
因为题目中的洗牌法并不存在单位元,所以强制加入一种所有牌都不变的洗牌法
对于每一个循环,他们内部的位置的染色必须是相同的
所以单独考虑每个循环染哪种颜色,可以通过一个类似背包的过程实现
周末晚会
Irena和Sirup正准备下个周末的Party。为这个Party,他们刚刚买了一个非常大的圆桌。他们想邀请每个人,但他们现在不知道如何分配座次。Irena说当有超过K个女孩座位相邻(即这些女孩的座位是连续的,中间没有男孩)的话,她们就会说一整晚的话而不和其他人聊天。 Sirup没有其他选择,只有同意她。然而,作为一名数学家,他很快地痴迷于所有可能方案。 题目说明: N个人围绕着圆桌坐着,其中一些是男孩,另一些是女孩。你的任务是找出所有合法的方案数,使得不超过K个女孩座位是连续的。 循环同构会被认为是同一种方案。对于100%的数据N,K < = 2000;mod 100000007
可以把循环看成 \(n\) 种置换
那么要统计的就是每一种置换下不动点个数的平均数
如果 \(n \leq k\) ,那么就没有任何限制,可以直接套一个 \(polya\) 引理
否则,就要用 \(dp\) 去统计方案
设 \(f[i]\) 为序列的首尾都放男孩,并且不超过 \(k\) 个女孩的座位是连续的方案数
转移也很简单, \(f[i]=\sum_{j=i-k-1}^{i-1}f[j]\)
统计答案的时候要从 \(1\) 到 \(n\) 枚举每一种置换 \(i\),那么循环节就是 \(gcd(i,n)\)
通过旋转这个循环节可以得到其它循环节
这些循环节是完全相同的,所以只需要统计一个循环节的答案即可
那么贡献就是 \(\sum_{j=gcd(i,n)-k}^{gcd(i,n)} f[j] \times (gcd(i,n)-j+1)\)
后面乘上的部分是因为我强制了第一个选男生,但实际上第一个位置是可以选女生的
我可以把后面的每一个女生都旋转到前面来
P4128 [SHOI2006] 有色图
图的同构问题
\(Polya\) 定理是用来解决点置换的,但是这道题要求的是边置换
那么就考虑边的两个端点分别在哪个循环中
分为两类:
\(1\)、边的两个端点在同一循环中
设循环的长度为 \(b\)
如果端点之间的间距不同,那么两条边一定不在一个等价类中
又因为是在循环中,所以间距 \(x\) 也可以看成间距 \(b-x\)
那么等价类的个数就是 \(\left\lfloor\frac{b}{2}\right\rfloor\)
\(2\)、边的两个端点在不同循环中
设这两个循环的长度分别为 \(b_1,b_2\)
每一个边的循环的大小都是 \(lcm(b_1,b_2)\)
那么边的等价类的个数就是 \(\frac{b_1b_2}{lcm(b_1,b_2)}=gcd(b_1,b_2)\)
设点的循环的长度为 \(b_1,b_2,b_2 \cdots b_k\)
那么最终的答案就是
现在的问题就是如何枚举 \(b\)
因为 \(n\) 的范围比较小,所以可以考虑 \(dfs\) 从大到小加数
对于每一个枚举出来的 \(b\) ,我们还要知道具体有多少置换是这样的
首先对于所有的点进行全排列,就是一个 \(n!\)
又因为每一个循环内部都是循环同构的,所以要除掉 \(b_i\)
而且我们强行给长度相同的循环规定了顺序
所以对于长度为 \(i\) 的循环,如果它出现了 \(s_i\) 次,还要给最后的结果除掉 \(s_i!\)
要除以的是给指数取模的时候要模 \(phi\) ,而不能模 \(mod\)

