洛谷 P4143 采集矿石 后缀数组
题目背景
ZRQ 成功从坍塌的洞穴中逃了出来。终于,他看到了要研究的矿石。他想挑一些带回去完成任务。
题目来源:Zhang_RQ哦对了 \(ZRQ\) 就他,嗯
题目描述
ZRQ 发现这里有 \(N\) 块排成一排的矿石。
他用一个小写字母来表示每块矿石,他还发现每块矿石有一个重要度 \(V_i\)。
ZRQ 想采集一段连续的矿石回研究所。
他非常严格,被采集的一段矿石必须满足小写字母的字典序降序排名等于这段矿石的重要度和。
这里多个出现在不同位置的本质相同串的字典序排名相同。
比如说字母串为 aa,那么第一个 a 的排名和第二个 a 的排名相同,都是 2(第 1 是 aa)。
ZRQ 问你,在原串中有哪些不同的子串可以被采集?
这里子串不同定义为出现位置不同,也就是说本质相同的子串出现在不同位置都要计算一次(当然重要度和等于排名是前提)。
比如共有 \(4\) 块矿石,小写字母串为 abcd,重要度各为 10 0 1 1。
我们把所有的子串按照字典序从大到小排名:1:d 2:cd 3:c 4:bcd 5:bc 6:b 7:abcd 8:abc 9:ab 10:a。
那么串 d 的排名为 \(1\)(第一大),重要度和为 \(1\),可以被采集。
串 cd 的排名为 \(2\),重要度和为 \(2\),可以被采集。
串 a 的排名为 \(10\),重要度和为 \(10\),可以被采集。
其他串则不满足这个条件,故有三个串可以被采集。
输入格式
第一行一个长度为 \(N\) 由小写字母组成的字符串,每个字符代表一个矿石。
第二行 \(N\) 个整数,表示 \(V_i\)。
输出格式
一行一个整数,表示能被采集的子串个数 \(S\)。
接下来 \(S\) 行每行两个整数 \(L,R\),分别表示每个可采集子串的左端点与右端点,按照左端点升序为第一关键字,右端点升序为第二关键字排序。
输入输出样例
输入 #1
abcd
10 0 1 1
输出 #1
3
1 1
3 4
4 4
输入 #2
aaaa
1 1 1 1
输出 #2
0
输入 #3
aaa
1 1 1
输出 #3
2
1 2
2 3
输入 #4
aaa
1 1 2
输出 #4
1
1 2
说明/提示
共 \(10\) 个测试点,每个点 \(10\) 分,计 \(100\) 分。
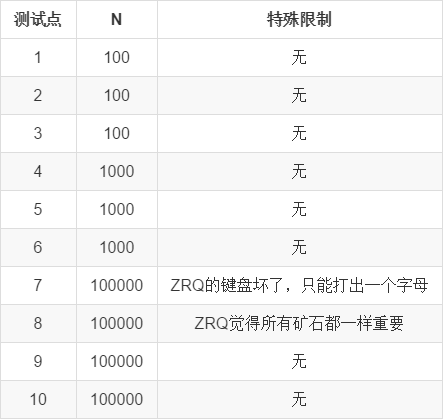
对于所有测试点,有 \(N\leq 10^5\),\(0 \le V_i \le 1000\)。保证每个点可被采集的子串不超过 \(10^5\) 个。
样例#1解释放在题面里了。
样例#2解释:
每个子串都不满足条件。
串 a 的排名是 \(4\),重要度和都是 \(1\)。
串 aa 的排名是 \(3\),重要度和都是 \(2\)。
串 aaa 的排名是 \(2\),重要度和都是 \(3\)。
串 aaaa 的排名是 \(1\),重要度和都是 \(4\)。
样例 #3解释:
串 a 的排名是 \(3\),重要度和都是 \(1\)。
串 aa 的排名是 \(2\),重要度和都是 \(2\),共有两个串aa,位置分别为 \(1 \sim 2\) 和 \(2 \sim3\)。
串 aaa 的排名是 \(1\),重要度和都是 \(3\)。
样例 #4解释:
可以发现,串 \(2 \sim 3\)(第二个 aa)不满足条件了。它的排名还是 \(2\) 不变,但是重要度和为 \(3\)。
分析
要求出所有排名等于重要度的子串并输出方案
首先可以证明这样的子串不会超过 \(n\) 个
因为假如我们固定了左端点,那么随着右端点的增大,重要度不会变小,但是排名会变小
因此对于一个确定的左端点,最多只会有一个右端点满足条件
又因为重要度和排名都是单调的,所以只需要固定左端点,二分合法的右端点就可以了
考虑如何快速求出一个子串的重要度和排名
重要度可以用前缀和 \(O(1)\) 查询
排名可以用后缀数组求出
在计算一个字符串的本质不同的子串时,我们会用到一个式子
\(\sum_{i=1}^nn-sa[i]+1-height[i]\)
一个很有用的性质就是这样求出的本质不同字串是按顺序的
所以对于一个子串,只需要算出它的前面有多少本质不同的子串即可
先用一个数组记录一下这个式子的前缀和,然后分情况讨论
设 \(fir[i]\) 为 \(i\) 号后缀的排名
如果 \(len \geq height[fir[l]]\),那么排名为 \(sum_{fir[l]}-(n-r)\)
否则向前二分找到一个位置 \(pos\),使得它恰好满足 \(len \geq height[pos]\),那么排名为 \((sum_{pos}-(n-sa[pos]-len+1))\)
后面减去的那一部分是左端点相同但是长度比当前子串长的
因为排名是按照字典序从大到小来的,所以还要拿总的本质不同的子串减去求出的结果
时间复杂度 \(O(nlog^2n)\)
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e5+5;
int sa[maxn],fir[maxn],sec[maxn],tax[maxn],n,heig[maxn],lg[maxn],mmin[maxn][20],m;
int a[maxn],sum1[maxn],sta1[maxn],sta2[maxn],tp;
char s[maxn];
long long tot,sum2[maxn];
void Qsort(){
for(rg int i=0;i<=m;i++) tax[i]=0;
for(rg int i=1;i<=n;i++) tax[fir[i]]++;
for(rg int i=1;i<=m;i++) tax[i]+=tax[i-1];
for(rg int i=n;i>=1;i--) sa[tax[fir[sec[i]]]--]=sec[i];
}
void getsa(){
m=1e5;
for(rg int i=1;i<=n;i++) fir[i]=s[i],sec[i]=i;
Qsort();
for(rg int len=1,p=0;p<n;len<<=1,m=p){
p=0;
for(rg int i=n-len+1;i<=n;i++) sec[++p]=i;
for(rg int i=1;i<=n;i++) if(sa[i]>len) sec[++p]=sa[i]-len;
Qsort();
memcpy(sec,fir,sizeof(sec));
fir[sa[1]]=p=1;
for(rg int i=2;i<=n;i++) fir[sa[i]]=(sec[sa[i]]==sec[sa[i-1]] && sec[sa[i]+len]==sec[sa[i-1]+len])?p:++p;
}
}
void getheight(){
rg int j,k=0;
for(rg int i=1;i<=n;i++){
if(k) k--;
j=sa[fir[i]-1];
while(s[i+k]==s[j+k]) k++;
heig[fir[i]]=k;
}
tot=1LL*n*(n+1)/2LL;
for(rg int i=2;i<=n;i++) tot-=heig[i];
for(rg int i=1;i<=n;i++) sum2[i]=sum2[i-1]+n-sa[i]+1-heig[i];
}
void pre(){
for(rg int i=1;i<=n;i++) mmin[i][0]=heig[i];
for(rg int i=2;i<=n;i++) lg[i]=lg[i>>1]+1;
for(rg int j=1;j<=18;j++){
for(rg int i=1;i+(1<<j)-1<=n;i++){
mmin[i][j]=std::min(mmin[i][j-1],mmin[i+(1<<(j-1))][j-1]);
}
}
}
int getans(rg int l,rg int r){
l++;
rg int k=lg[r-l+1];
return std::min(mmin[l][k],mmin[r-(1<<k)+1][k]);
}
int getval(rg int l,rg int r){
return sum1[r]-sum1[l-1];
}
long long getrk(rg int l,rg int r){
rg int len=r-l+1;
if(heig[fir[l]]<=len) return tot-(sum2[fir[l]]-(n-r))+1;
rg int nl=1,nr=fir[l]-1,mids;
while(nl<=nr){
mids=(nl+nr)>>1;
if(getans(mids,fir[l])<=len) nl=mids+1;
else nr=mids-1;
}
return tot-(sum2[nr]-(n-sa[nr]-len+1))+1;
}
void solve(rg int id){
rg int l=id,r=n,mids;
while(l<=r){
mids=(l+r)>>1;
if(getrk(id,mids)==getval(id,mids)){
sta1[++tp]=id,sta2[tp]=mids;
return;
} else if(getrk(id,mids)>getval(id,mids)){
l=mids+1;
} else {
r=mids-1;
}
}
}
int main(){
scanf("%s",s+1);
n=strlen(s+1);
for(rg int i=1;i<=n;i++) a[i]=read();
getsa(),getheight(),pre();
for(rg int i=1;i<=n;i++) sum1[i]=sum1[i-1]+a[i];
for(rg int i=1;i<=n;i++) solve(i);
printf("%d\n",tp);
for(rg int i=1;i<=tp;i++) printf("%d %d\n",sta1[i],sta2[i]);
return 0;
}


