省选测试10
总结

三道毒瘤题,部分分很少,数据很强
全场暴力分,赞美良心出题人
A. 鱼死网破(clash)
分析
对于每一个墙,开一个 \(vector\) 存储在墙上方的点与墙左右两端连线的向量
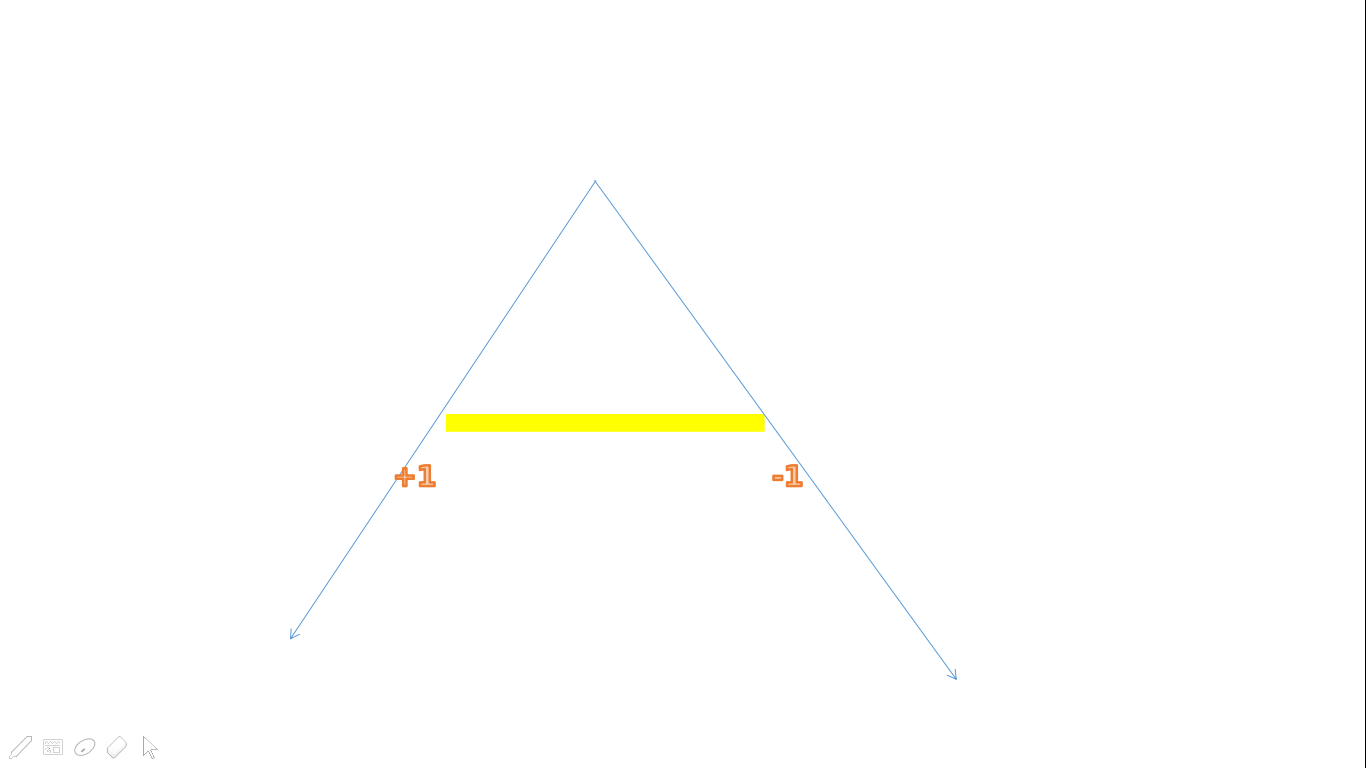
把左侧向量的权值设为 \(+1\),把右侧向量的权值设为 \(-1\)
按照极角排序
对于在 \(x\) 轴下方的点,它不能看到的所有的点就是它左侧所有向量的权值和
二分查找一下就行了
但是有可能一个点会被算多次
所以对于每一个点,用类似括号匹配的方式去掉重合的
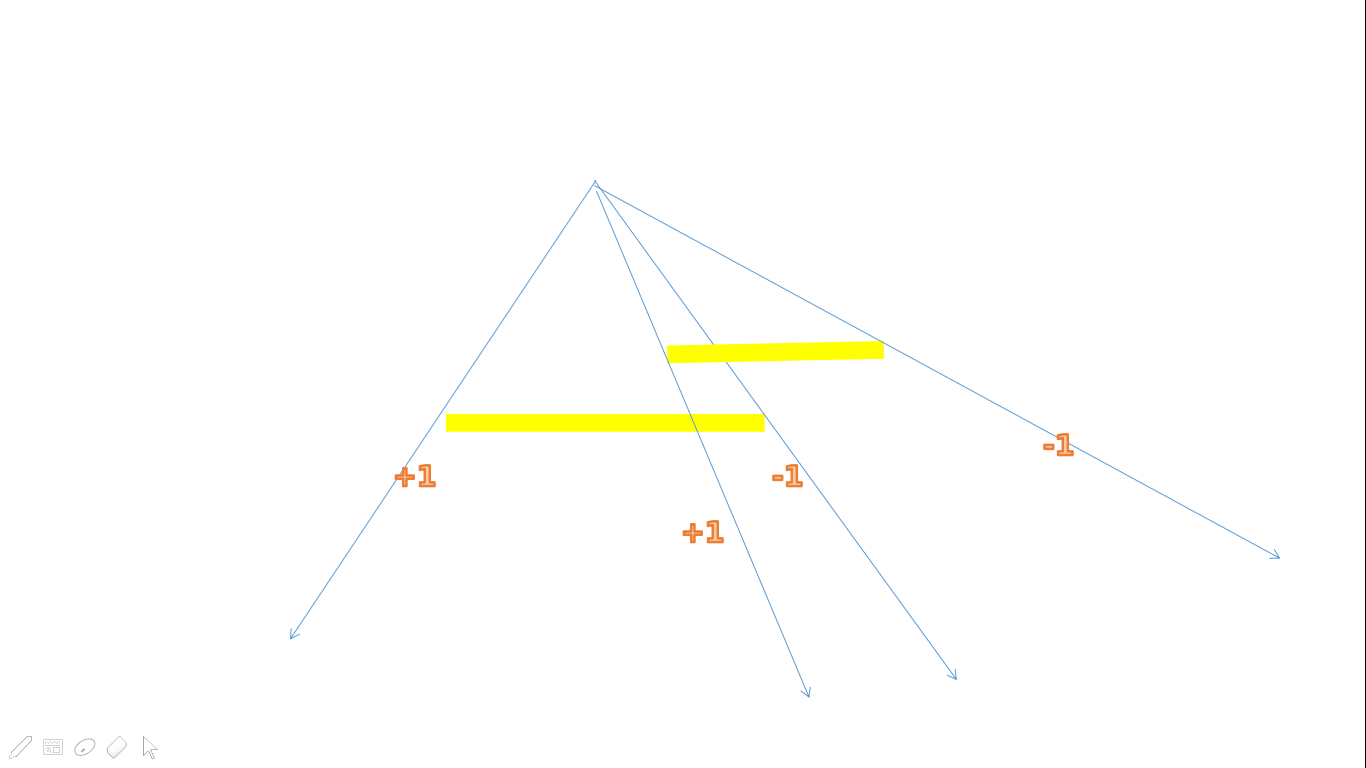
比如说上面这幅图,我只要最左边的和最右边的
代码
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e5+5;
int n,k,m,op,x[maxn],y[maxn],latans,tp;
struct jie{
int l,r,wz;
}b[maxn];
struct Node{
double x,y;
int op;
Node(){}
Node(rg double aa,rg double bb,rg int cc){
x=aa,y=bb,op=cc;
}
friend double operator ^(const Node& A,const Node& B){
return A.x*B.y-B.x*A.y;
}
friend bool operator <(const Node& A,const Node& B){
return (A^B)>0;
}
}sta[maxn];
std::vector<Node> v1[maxn],v2[maxn];
int solve(rg int nx,rg int ny){
rg Node tmp;
rg int ans=0;
for(rg int i=1;i<=k;i++){
tmp=Node(b[i].l-nx,b[i].wz-ny,1);
ans+=std::upper_bound(v1[i].begin(),v1[i].end(),tmp)-v1[i].begin();
tmp=Node(b[i].r-nx,b[i].wz-ny,1);
ans-=std::lower_bound(v2[i].begin(),v2[i].end(),tmp)-v2[i].begin();
}
return n-ans;
}
int main(){
n=read(),k=read(),m=read(),op=read();
for(rg int i=1;i<=n;i++) x[i]=read(),y[i]=read();
for(rg int i=1;i<=k;i++){
b[i].l=read(),b[i].r=read(),b[i].wz=read();
if(b[i].l>b[i].r) std::swap(b[i].l,b[i].r);
}
for(rg int i=1;i<=n;i++){
tp=0;
for(rg int j=1;j<=k;j++){
if(b[j].wz<y[i]){
sta[++tp]=Node(x[i]-b[j].l,y[i]-b[j].wz,j);
sta[++tp]=Node(x[i]-b[j].r,y[i]-b[j].wz,-j);
}
}
std::sort(sta+1,sta+tp+1);
rg int tmp=0;
for(rg int j=1;j<=tp;j++){
if(tmp==0 && sta[j].op>0){
v1[sta[j].op].push_back(sta[j]);
} else if(tmp==1 && sta[j].op<0){
v2[-sta[j].op].push_back(sta[j]);
}
if(sta[j].op>0) tmp++;
else tmp--;
}
}
for(rg int i=1;i<=k;i++){
std::sort(v1[i].begin(),v1[i].end());
std::sort(v2[i].begin(),v2[i].end());
}
rg int aa,bb;
for(rg int i=1;i<=m;i++){
aa=read(),bb=read();
if(op) aa^=latans,bb^=latans;
printf("%d\n",latans=solve(aa,bb));
}
return 0;
}
B.漏网之鱼(escape)
分析
线段树基础练习题
首先,对于权值 \(>n+1\) 的 \(a[i]\) ,我们直接把它设为 \(n+1\) 就行了
因为 \(mex\) 肯定不会大于 \(n\)
所以我们就可以用一个 \(vector\) 存一下 \(a[i]\) 出现的位置
对于特殊性质 \(D\),只有一次询问
开一棵线段树维护 \(mex\) 的区间和
其中下表为 \(i\) 的叶子节点存储区间 \([tim,i]\) 的 \(mex\) 值
\(tim\) 为当前左端点移动到了哪一个位置
首先,我们可以用 \(O(n)\) 的复杂度预处理出左端点在 \(1\) 的时候区间 \([1,i]\) 的所有 \(mex\) 值
用预处理出来的这些 \(mex\) 值建好树
然后考虑左端点移动时的贡献
当左端点由位置 \(i\) 移动到位置 \(i+1\) 的时候
区间 \([i,nxt[a[i]]-1]\) 都不会再有 \(a[i]\) 的贡献
\(nxt[a[i]]\) 表示 \(a[i]\) 下一次出现的位置
所以它们的 \(mex\) 值要和 \(a[i]\) 取个 \(min\)
根据 \(mex\) 函数的性质,在线段树上从左到右, \(mex\) 一定是单调不减的
所以我们区间取 \(min\) 的操作不会改变单调性
记录一个最大值,然后在线段树上二分查找第一个大于 \(a[i]\) 的位置,区间赋值就行了
每一次移动左端点的时候统计一下答案就可以了
考虑如何扩展到多组询问的情况
我们可以参照主席树的思想,当左端点在 \(tim\) 时
存储的不再是当前的值,而是历史信息和
所以我们可以把一组询问拆成两个,当 \(tim=r\) 的时候加一下区间 \([l,r]\) 的贡献
当 \(tim=l-1\) 的时候减去区间 \([l,r]\) 的贡献
问题就是如何维护历史信息和
考虑在没有修改操作时,某一个节点的贡献可以看成一个一次函数的形式
因为随着时间的变化,它的增长率是一定的
而且一次函数有一个很好的性质就是它满足可加性
我们当前区间的所有 \(k\) 和 \(b\) 加起来当一个一次函数算和分开算的结果是一样的
所以就可以维护一个 \(sumk\) 和 \(sumb\) 代表区间内所有的 \(k\) 和 \(b\) 之和
问题在于如何处理修改操作
首先斜率 \(k\) 是要由原来的值变为 \(a[i]\) 的
所以我们维护一个 \(k\) 区间加的标记
因为 \(k\) 变了,所以 \(b\) 也要跟着变
我们再维护一个 \(b\) 区间加的标记就行了
其实这东西可以看成一个分段函数的形式
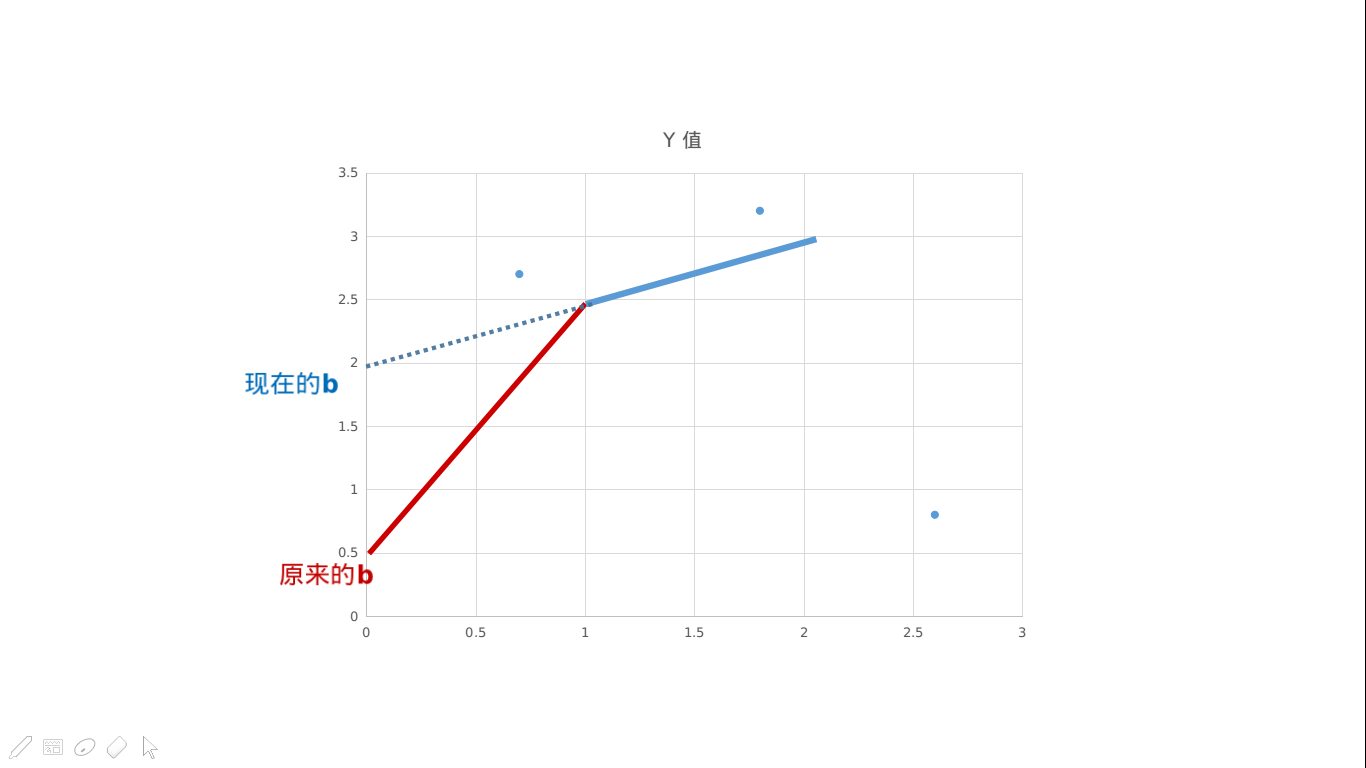
结合图可能更好理解一些
要注意的时,我们更改函数值之后把之前的 \(tim\) 带入算出来的结果就不对了
所以要把询问按照 \(tim\) 从小到大排序
这样就不会影响结果了,因为我们只要现在对和之后对,不用管之前对不对
递归的时候如果整段区间的值都相同整体打标记就行了
代码
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
#include<cstring>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5;
int typ,n,a[maxn],cnt[maxn],val[maxn],tim,q,tp;
std::vector<int> g[maxn];
long long ans[maxn];
struct trr{
int l,r,mmin,mmax,siz;//左端点,右端点,区间最大,区间最小,区间长度
long long sumk,sumb,laz,lazb,lazk;//k的和,b的和,区间赋值标记,b区间加标记,k区间加标记
}tr[maxn<<2];
void push_up(rg int da){
tr[da].mmin=std::min(tr[da<<1].mmin,tr[da<<1|1].mmin);
tr[da].mmax=std::max(tr[da<<1].mmax,tr[da<<1|1].mmax);
tr[da].sumb=tr[da<<1].sumb+tr[da<<1|1].sumb;
tr[da].sumk=tr[da<<1].sumk+tr[da<<1|1].sumk;
}
void push_down(rg int da){
if(tr[da].laz!=-1){
tr[da<<1].laz=tr[da<<1|1].laz=tr[da].laz;
tr[da<<1].mmin=tr[da<<1|1].mmin=tr[da].laz;
tr[da<<1].mmax=tr[da<<1|1].mmax=tr[da].laz;
tr[da].laz=-1;
}
if(tr[da].lazb){
tr[da<<1].sumb+=tr[da<<1].siz*tr[da].lazb;
tr[da<<1].lazb+=tr[da].lazb;
tr[da<<1|1].sumb+=tr[da<<1|1].siz*tr[da].lazb;
tr[da<<1|1].lazb+=tr[da].lazb;
tr[da].lazb=0;
}
if(tr[da].lazk){
tr[da<<1].sumk+=tr[da<<1].siz*tr[da].lazk;
tr[da<<1].lazk+=tr[da].lazk;
tr[da<<1|1].sumk+=tr[da<<1|1].siz*tr[da].lazk;
tr[da<<1|1].lazk+=tr[da].lazk;
tr[da].lazk=0;
}
}
void build(rg int da,rg int l,rg int r){
tr[da].l=l,tr[da].r=r,tr[da].siz=r-l+1,tr[da].laz=-1;
if(tr[da].l==tr[da].r){
tr[da].mmax=tr[da].mmin=tr[da].sumk=val[l];
return;
}
rg int mids=(l+r)>>1;
build(da<<1,l,mids);
build(da<<1|1,mids+1,r);
push_up(da);
}
void xg(rg int da,rg int l,rg int r,rg int val){
if(tr[da].l!=tr[da].r) push_down(da);
if(tr[da].mmax<=val) return;
if(tr[da].l>=l && tr[da].r<=r && tr[da].mmin==tr[da].mmax){
tr[da].lazk=val-tr[da].mmin;//更改k
tr[da].lazb=1LL*tim*(tr[da].mmin-val);//顺便改一下b
tr[da].mmin=tr[da].mmax=tr[da].laz=val;
tr[da].sumk+=tr[da].lazk*tr[da].siz;
tr[da].sumb+=tr[da].lazb*tr[da].siz;
return;
}
rg int mids=(tr[da].l+tr[da].r)>>1;
if(l<=mids) xg(da<<1,l,r,val);
if(r>mids) xg(da<<1|1,l,r,val);
push_up(da);
}
long long cx(rg int da,rg int l,rg int r){
if(tr[da].l!=tr[da].r) push_down(da);
if(tr[da].l>=l && tr[da].r<=r){
return tr[da].sumk*tim+tr[da].sumb;
}
rg int mids=(tr[da].l+tr[da].r)>>1;
rg long long nans=0;
if(l<=mids) nans+=cx(da<<1,l,r);
if(r>mids) nans+=cx(da<<1|1,l,r);
return nans;
}
struct jie{
int l,r,id,op,rt;
jie(){}
jie(rg int aa,rg int bb,rg int cc,rg int dd,rg int ee){
l=aa,r=bb,id=cc,op=dd,rt=ee;
}
}b[maxn<<1];
bool cmp(rg jie aa,rg jie bb){
return aa.rt<bb.rt;
}
int main(){
typ=read(),n=read();
for(rg int i=1;i<=n;i++) a[i]=read();
for(rg int i=1;i<=n;i++) if(a[i]>n+1) a[i]=n+1;
for(rg int i=1;i<=n;i++) cnt[a[i]]++;
rg int now=0;
while(cnt[now]) now++;
val[n]=now;
for(rg int i=n-1;i>=1;i--){
cnt[a[i+1]]--;
if(cnt[a[i+1]]==0) now=std::min(now,a[i+1]);
val[i]=now;
}//把左端点为1的答案预处理出来
for(rg int i=0;i<=n+1;i++) g[i].push_back(n+1);
for(rg int i=n;i>=1;i--) g[a[i]].push_back(i);//方便求nxt
build(1,1,n);
q=read();
rg int aa,bb,head=1;
for(rg int i=1;i<=q;i++){
aa=read(),bb=read();
b[++tp]=jie(aa,bb,i,-1,aa-1);
b[++tp]=jie(aa,bb,i,1,bb);
}//差分
std::sort(b+1,b+1+tp,cmp);
while(b[head].rt==0 && head<=tp) head++;
for(tim=1;tim<=n;tim++){
while(b[head].rt==tim && head<=tp){
ans[b[head].id]+=b[head].op*cx(1,b[head].l,b[head].r);
head++;
}
g[a[tim]].pop_back();
xg(1,tim,g[a[tim]][g[a[tim]].size()-1]-1,a[tim]);
xg(1,tim,tim,0);
}
for(rg int i=1;i<=q;i++){
printf("%lld\n",ans[i]);
}
return 0;
}
C.浑水摸鱼(waterflow)
分析
将字符串的哈希值定义为每个位置的下一个与其相同的值的位置差 \(\times w^i\)
\(w\) 为当前字符所处的位置
这样定义和最小表示法是等价的
然后就可以拿线段树维护哈希值
根据哈希值的大小对后缀进行排序
答案就是总的字串的数量减去相邻两后缀之间相同的部分
相同的部分可以二分求
有些卡常
代码
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
typedef unsigned long long ull;
const ull bas=23333;
const int maxn=5e4+5;
int rt[maxn],cnt,sa[maxn],lst[maxn],nxt[maxn],dis[maxn],n,a[maxn];
ull mi[maxn],ny[maxn],inv;
ull ksm(rg ull ds,rg ull zs){
rg ull nans=1;
while(zs){
if(zs&1) nans=nans*ds;
ds=ds*ds;
zs>>=1;
}
return nans;
}
struct trr{
int lch,rch;
ull val;
}tr[maxn*20];
void build(rg int &da,rg int l,rg int r){
da=++cnt;
if(l==r) return tr[da].val=mi[l]*(dis[l]+1),void();
rg int mids=(l+r)>>1;
build(tr[da].lch,l,mids);
build(tr[da].rch,mids+1,r);
tr[da].val=tr[tr[da].lch].val+tr[tr[da].rch].val;
}
void ad(rg int &da,rg int pre,rg int wz,rg int l,rg int r){
da=++cnt;
tr[da]=tr[pre];
if(l==r) return tr[da].val=mi[l],void();
rg int mids=(l+r)>>1;
if(wz<=mids) ad(tr[da].lch,tr[pre].lch,wz,l,mids);
else ad(tr[da].rch,tr[pre].rch,wz,mids+1,r);
tr[da].val=tr[tr[da].lch].val+tr[tr[da].rch].val;
}
ull cx(rg int da,rg int nl,rg int nr,rg int l,rg int r){
if(l>=nl && r<=nr) return tr[da].val;
rg int mids=(l+r)>>1;
rg ull nans=0;
if(nl<=mids) nans+=cx(tr[da].lch,nl,nr,l,mids);
if(nr>mids) nans+=cx(tr[da].rch,nl,nr,mids+1,r);
return nans;
}
ull gethash(rg int l,rg int r){
return cx(rt[l],l,r,1,n)*ny[l];
}
bool cmp(rg int aa,rg int bb){
rg int l=1,r=n-std::max(aa,bb)+1,mids;
while(l<=r){
mids=(l+r)>>1;
if(gethash(aa,aa+mids-1)==gethash(bb,bb+mids-1)) l=mids+1;
else r=mids-1;
}
return (aa+r-dis[aa+r]<aa?0:dis[aa+r])<(bb+r-dis[bb+r]<bb?0:dis[bb+r]);
//这里也可以比较哈希值,因为被卡常就直接按照定义比较了
}
int main(){
n=read();
for(rg int i=1;i<=n;i++) a[i]=read();
mi[0]=ny[0]=1,inv=ksm(bas,(1ull<<63)-1);
for(rg int i=1;i<=n;i++){
mi[i]=mi[i-1]*bas;
ny[i]=ny[i-1]*inv;
sa[i]=i;
}
for(rg int i=1;i<=n;i++){
if(lst[a[i]]==0){
dis[i]=0;
} else {
dis[i]=i-lst[a[i]];
}
nxt[lst[a[i]]]=i;
lst[a[i]]=i;
}
build(rt[1],1,n);
for(rg int i=2;i<=n;i++){
rt[i]=rt[i-1];
if(nxt[i-1]) ad(rt[i],rt[i-1],nxt[i-1],1,n);
}
std::stable_sort(sa+1,sa+1+n,cmp);
rg long long ans=1LL*(n+1)*n/2LL;
for(rg int i=2;i<=n;i++){
rg int l=1,r=n-std::max(sa[i],sa[i-1])+1,mids;
while(l<=r){
mids=(l+r)>>1;
if(gethash(sa[i-1],sa[i-1]+mids-1)==gethash(sa[i],sa[i]+mids-1)) l=mids+1;
else r=mids-1;
}
ans-=r;
}
printf("%lld\n",ans);
return 0;
}

