容斥原理学习笔记
获得更好的阅读体验,请开启夜间模式
定义
在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
一、普通容斥
公式
设 \(U\) 中元素有 \(n\) 种不同的属性,而第 \(i\) 种属性称为 \(P_i\),拥有属性\(P_i\) 的元素构成集合\(S_i\) ,那么
即
大概的思想就是奇加偶减,用单个元素之和减去两个集合相交的部分,再减去三个集合相交的部分,再加上四个集合相交的部分
证明
对于每个元素使用二项式定理计算其出现的次数。对于元素 \(x\),假设它出现在\(T_1,T_2,T_3...\)的集合中,那么它的出现次数为
以上引用自OI-WIKI
例题一:八
题目描述
八是个很有趣的数字啊。
八=发,八八=爸爸,\(88\)=拜拜。
当然最有趣的还是 \(8\)
用二进制表示是 \(1000\)。
怎么样,有趣吧。当然题目和这些都没有关系。
某个人很无聊,他想找出 \([a,b]\)中能被 \(8\)整除却不能被其他一些数整除的数。
输入格式
第一行一个数 \(n\),代表不能被整除的数的个数。
第二行 \(n\)个数,中间用空格隔开。
第三行两个数 \(a,b\),中间一个空格。
输出格式
一个整数,为 \([a,b]\)间能被 整除却不能被那 \(n\)个数整除的数的个数。
样例
样例输入
3
7764 6082 462
2166 53442
样例输出
6378
数据范围与提示
对于 \(30\%\)的数据, \(1⩽n⩽5,1⩽a⩽b⩽10^5\)。
对于 \(100\%\)的数据,\(1⩽n⩽15,1⩽a⩽b⩽10^9\) 。\(n\)个数全都小于等于 \(10^4\) 大于等于 \(1\) 。
分析
我们先算出 \([l,r]\) 中能被 \(8\) 整除的数的个数,再减去能被 \(8\)和 \(n\) 个数中任意一个数整除的数的个数,再加上能被 \(8\)和 \(n\) 个数中任意两个数整除的数的个数,依此类推
代码
#include<cstdio>
#define rg register
const int maxn=18;
int a[maxn],n,l,r,mmax,ans;
long long gcd(long long aa,long long bb){
if(bb==0) return aa;
return gcd(bb,aa%bb);
}
long long lcm(long long aa,long long bb){
return 1LL*aa/gcd(aa,bb)*bb;
}
int main(){
scanf("%d",&n);
for(rg int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
scanf("%d%d",&l,&r);
mmax=(1<<n)-1;
ans=r/8-(l-1)/8;
rg long long now;
rg int cnt;
for(int i=1;i<=mmax;i++){
now=8,cnt=0;
for(rg int j=1;j<=n;j++){
if(i&(1<<(j-1))){
now=lcm(now,(long long)a[j]);
if(now>r) break;
cnt++;
}
}
if(cnt&1) ans-=(1LL*r/now-1LL*(l-1)/now);
else ans+=(1LL*r/now-1LL*(l-1)/now);
}
printf("%d\n",ans);
return 0;
}
例题二、建设城市
题目描述
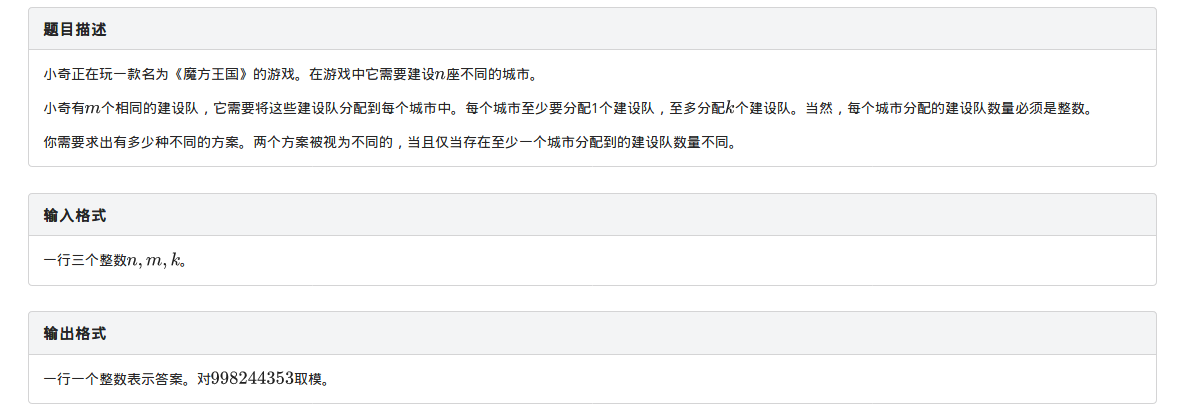
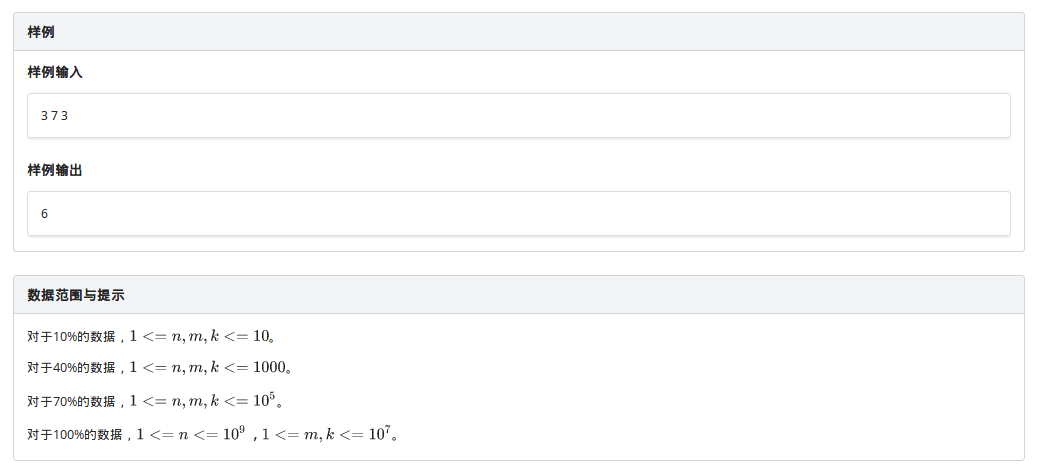
分析
如果我们不考虑最多选 \(k\) 个施工队的限制的话,那么总方案数为 \(C_{m-1}^{n-1}\)(根据隔板法)
现在我们要做的就是求出不满足限制的方案数
我们可以分别算出至少有 \(i\) 座城市不满足限制的方案数 \(C_n^i \times C{m-1-k\times i}^{n-1}\)
含义是先从 \(n\) 座城市里选出 \(i\) 座城市,再从剩下的 \(m-1-k\times i\) 个空位中选出 \(n-1\) 个空位
在根据容斥原理求出不满足条件的方案数
用总方案数一减就可以了
代码
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<iostream>
#define rg register
const int mod=998244353;
const int maxn=1e7+5;
int n,m,k,ny[maxn],jc[maxn],jcc[maxn],ans;
int getC(int nn,int mm){
return 1LL*jc[nn]*jcc[nn-mm]%mod*jcc[mm]%mod;
}
int main(){
scanf("%d%d%d",&n,&m,&k);
if(m<n || 1LL*n*k<1LL*m){
printf("0\n");
return 0;
}
ny[1]=1;
for(rg int i=2;i<maxn;i++){
ny[i]=1LL*(mod-mod/i)*ny[mod%i]%mod;
}
jc[0]=jcc[0]=1;
for(rg int i=1;i<maxn;i++){
jc[i]=1LL*jc[i-1]*i%mod;
jcc[i]=1LL*jcc[i-1]*ny[i]%mod;
}
ans=getC(m-1,n-1);
for(rg int i=1;i<=n;i++){
if(m-i*k<n) break;
if(i&1) ans-=1LL*getC(n,i)*getC(m-i*k-1,n-1)%mod;
else ans+=1LL*getC(n,i)*getC(m-i*k-1,n-1)%mod;
if(ans<mod) ans+=mod;
if(ans>=mod) ans-=mod;
}
printf("%d\n",ans);
return 0;
}
例题三、P1450 [HAOI2008]硬币购物
题目描述
分析
同样的方法,我们可以预处理出没有硬币个数限制的方案数,即完全背包
再通过容斥原理求出不满足限制的方案数
代码
#include<cstdio>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
typedef long long ll;
const int maxn=1e5+5;
ll f[maxn],ans;
int c[maxn],d[maxn],n,s;
int main(){
c[1]=read(),c[2]=read(),c[3]=read(),c[4]=read();
n=read();
f[0]=1;
for(rg int i=1;i<=4;i++){
for(rg int j=c[i];j<maxn;j++){
f[j]+=f[j-c[i]];
}
}
int now=0,nans=0;
for(rg int i=1;i<=n;i++){
ans=0;
d[1]=read(),d[2]=read(),d[3]=read(),d[4]=read(),s=read();
for(rg int j=1;j<=15;j++){
now=0,nans=0;
for(rg int k=1;k<=4;k++){
if(j&(1<<(k-1))){
now++;
nans+=(d[k]+1)*c[k];
}
}
if(s>=nans){
if(now&1) ans+=f[s-nans];
else ans-=f[s-nans];
}
}
ans=f[s]-ans;
printf("%lld\n",ans);
}
return 0;
}
二、Min-max 容斥
公式
对于全序集合\(S\),有

以上引用自OI-WIKI
证明
对于第一个式子
我们设 \(A_k\) 为 \(U\) 内元素降序排序后排名第 \(k\) 的元素,也就是第 \(k\) 大。
若 \(k=1\) ,那么 \(A_1\) 作为最小值只会出现一次 ,系数为\(1\)
若 \(k>1\),那么 \(A_k\) 作为最小值会出现 \(2^{k-1}\) 次,其中有 \(2^{k-2}\) 次出现在元素个数为偶数的序列中,另外的\(2^{k-2}\)次出现在元素个数为奇数的序列中
最终加和的结果即为 \(A_1\)
对于第二个式子也是同理
这个东西主要用在期望题中,因为期望下的 \(\min\)和\(\max\)是很难求的
例题、礼物
题目描述
夏川的生日就要到了。作为夏川形式上的男朋友,季堂打算给夏川买一些生日礼物。商店里一共有种礼物。夏川每得到一种礼物,就会获得相应喜悦值 \(W_i\)(每种礼物的喜悦值不能重复获得)。每次,店员会按照一定的概率 \(P_i\)(或者不拿出礼物),将第 \(i\)种礼物拿出来。季堂每次都会将店员拿出来的礼物买下来。没有拿出来视为什么都没有买到,也 算一次购买。
众所周知,白毛切开都是黑的。所以季堂希望最后夏川的喜悦值尽可能地高。
求夏川最后最大的喜悦值是多少,并求出使夏川得到这个喜悦值,季堂的期望购买次数。
输入格式
第一行,一个整数 \(N\),表示有 \(N\) 种礼物。
接下来 \(N\)行,每行一个实数 \(P_i\)和正整数 \(W_i\),表示第 \(i\) 种礼物被拿出来的概率和可以获得喜悦值。
输出格式
第一行,一个整数表示可以获得的最大喜悦值。
第二行,一个实数表示获得这个喜悦值的期望购买次数,保留 \(3\) 位小数。
样例
样例输入
3
0.1 2
0.2 5
0.3 7
样例输出
14
12.167
数据范围与提示
对于 \(10\%\)的数据, \(N=1\)
对于 \(30\%\) 的数据, \(N\le5\)
对于 \(100\%\)的数据, \(N \le 25 ,0 < Wi \le 10^9 ,0 < Pi \le 1\text{且}\sum P_i \le 1\)
分析
显然第一问应该输出所有礼物的喜悦值之和
对于第二问,用\(max\)代表将集合里的礼物全部买齐的期望,用 \(min\)代表买到集合中礼物任意一件的期望
套一下式子就可以了
代码
#include<cstdio>
const int maxn=30;
int a[maxn],n;
double p[maxn],ans2;
long long ans1;
void dfs(int now,double sum,int cnt){
if(now>n){
if(cnt&1) ans2+=1.0/sum;
else if(cnt) ans2-=1.0/sum;
return;
}
dfs(now+1,sum+p[now],cnt+1);
dfs(now+1,sum,cnt);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lf%d",&p[i],&a[i]);
ans1=ans1+a[i];
}
printf("%lld\n",ans1);
dfs(1,0,0);
printf("%.3f\n",ans2);
return 0;
}

