联考day6 D. 模板 树上启发式合并+线段树二分
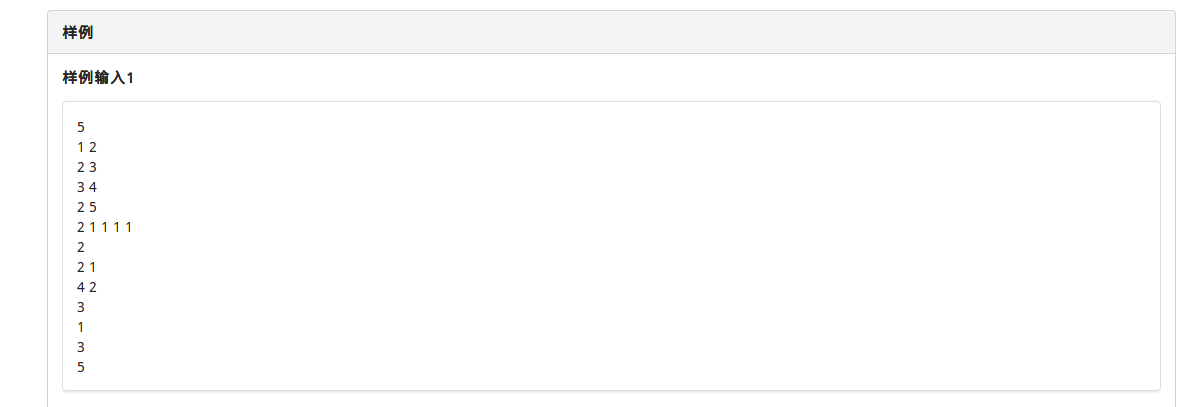
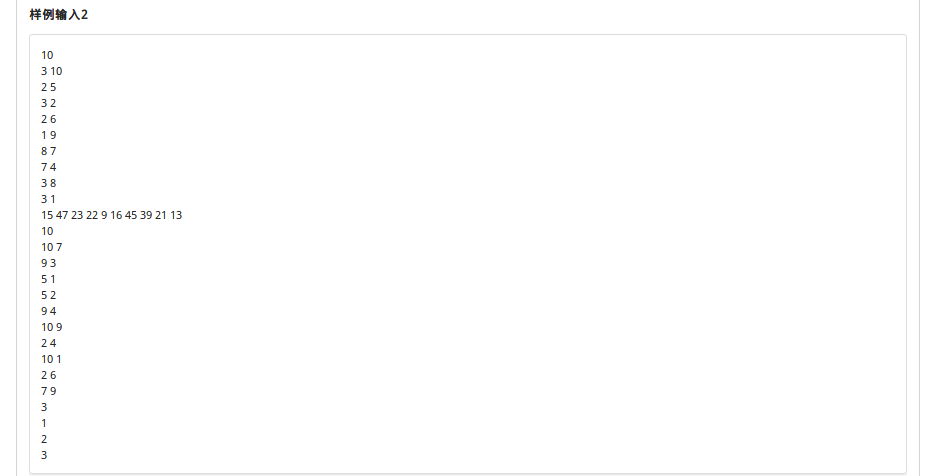
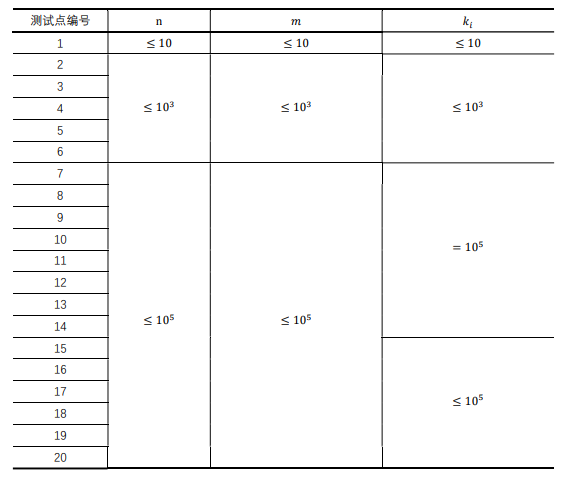
题目描述




分析
因为一个节点被放了小球后,它的所有祖先节点都要放小球
所以我们可以在递归的时候再把儿子的贡献上传
对于没有小桶限制的情况,显然是一个 \(dsu\) 的板子
对于有小桶限制的情况,关键是怎么处理重复的颜色
我们可以开一个数组记录一下当前颜色最早出现在哪一次操作中
统计当前颜色答案的时候只计算这一次操作
统计小球个数的时候所有的操作都要计算
所以我们可以用线段树维护,线段树的下标为操作的时间
线段树记录两个变量,一个是当前节点代表的区间有多少个小球
一个是当前节点代表的区间中有多少小球是最早出现的,这一部分要记录在答案中
统计答案的时候不断在线段树上二分递归
然后就是板子了
代码
#include<cstdio>
#include<cstring>
#include<bitset>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<vector>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5,maxm=2e3+5;
int h[maxn],tot=1,k[maxn];
struct asd{
int to,nxt;
}b[maxn];
void ad(int aa,int bb){
b[tot].to=bb;
b[tot].nxt=h[aa];
h[aa]=tot++;
}
int n,m,q,sta[maxn],tp,mintim[maxn];
struct jie{
int id,col;
jie(){}
jie(int aa,int bb){
id=aa,col=bb;
}
}c[maxn];
struct trr{
int l,r,cnt,ans;
}tr[maxn];
struct jie2{
int tim,col;
jie2(){}
jie2(int aa,int bb){
tim=aa,col=bb;
}
};
void push_up(int da){
tr[da].cnt=tr[da<<1].cnt+tr[da<<1|1].cnt;
tr[da].ans=tr[da<<1].ans+tr[da<<1|1].ans;
}
void build(int da,int l,int r){
tr[da].l=l,tr[da].r=r;
if(tr[da].l==tr[da].r){
tr[da].cnt=tr[da].ans=0;
return;
}
rg int mids=(tr[da].l+tr[da].r)>>1;
build(da<<1,l,mids);
build(da<<1|1,mids+1,r);
}
void xg(int da,int wz,int adt,int ada){
if(tr[da].l==tr[da].r){
tr[da].cnt+=adt;
tr[da].ans+=ada;
return;
}
rg int mids=(tr[da].l+tr[da].r)>>1;
if(wz<=mids) xg(da<<1,wz,adt,ada);
else xg(da<<1|1,wz,adt,ada);
push_up(da);
}
int cx(int da,int maxt){
if(tr[da].cnt==maxt) return tr[da].ans;
if(tr[da<<1].cnt>=maxt) return cx(da<<1,maxt);
else return tr[da<<1].ans+cx(da<<1|1,maxt-tr[da<<1].cnt);
}
int f[maxn],son[maxn],siz[maxn],dep[maxn];
void dfs1(int now,int fa){
f[now]=fa;
dep[now]=dep[fa]+1;
siz[now]=1;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(u==fa) continue;
dfs1(u,now);
siz[now]+=siz[u];
if(son[now]==0 || siz[u]>siz[son[now]]){
son[now]=u;
}
}
}
std::vector<jie2> g[maxn];
int orz,ans[maxn];
void xg(int now,int op){
if(op==0){
for(rg int i=0;i<g[now].size();i++){
rg int ac1=g[now][i].tim,ac2=g[now][i].col;
if(ac1==mintim[ac2]){
xg(1,ac1,-1,-1);
mintim[ac2]=0x3f3f3f3f;
} else {
xg(1,ac1,-1,0);
}
}
} else {
for(rg int i=0;i<g[now].size();i++){
rg int ac1=g[now][i].tim,ac2=g[now][i].col;
if(ac1<mintim[ac2]){
if(mintim[ac2]!=0x3f3f3f3f) xg(1,mintim[ac2],0,-1);
mintim[ac2]=ac1;
xg(1,mintim[ac2],1,1);
} else {
xg(1,ac1,1,0);
}
}
}
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(u==f[now] || u==orz) continue;
xg(u,op);
}
}
void dfs2(int now,int op){
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(u==f[now] || u==son[now]) continue;
dfs2(u,0);
}
if(son[now]){
dfs2(son[now],1);
orz=son[now];
}
xg(now,1);
orz=0;
ans[now]=cx(1,std::min(k[now],tr[1].cnt));
if(op==0){
xg(now,0);
}
}
int main(){
freopen("ac.in","r",stdin);
freopen("ac.out","w",stdout);
memset(h,-1,sizeof(h));
memset(mintim,0x3f,sizeof(mintim));
n=read();
rg int aa,bb;
for(rg int i=1;i<n;i++){
aa=read(),bb=read();
ad(aa,bb);
ad(bb,aa);
}
for(rg int i=1;i<=n;i++){
k[i]=read();
}
m=read();
for(rg int i=1;i<=m;i++){
c[i].id=read();
c[i].col=read();
sta[++tp]=c[i].col;
}
std::sort(sta+1,sta+1+tp);
tp=std::unique(sta+1,sta+1+m)-sta-1;
for(rg int i=1;i<=m;i++){
c[i].col=std::lower_bound(sta+1,sta+1+tp,c[i].col)-sta;
}
build(1,1,m);
dfs1(1,0);
for(rg int i=1;i<=m;i++){
g[c[i].id].push_back(jie2(i,c[i].col));
}
dfs2(1,0);
q=read();
for(rg int i=1;i<=q;i++){
aa=read();
printf("%d\n",ans[aa]);
}
return 0;
}


