算法数据结构03 /二分查找、排序算法

算法数据结构03 /二分查找、排序算法

目录

• 算法数据结构03 /二分查找、排序算法
  • 1. 二分查找
  • 2. 排序算法
  • 3.排序算法总结

1. 二分查找

• 二分查找：只能作用在有序集合

• 代码实现：

  def middle(alist,item):
      find = False
      low = 0
      high = len(alist)-1
      
      while not find and low <= high:  # 要加=号
          mid = (low+high)//2 # 中间元素下标
          # 查找的值大于中间元素的值，意味着查找的值只可能出现在中间值的右侧
          if item > alist[mid]:
              low = mid + 1
          # 查找的值和中间元素相等，意味着找到了
          elif item == alist[mid]:
              find = True
          # 查找的值小于中间元素的值，意味着查找的值只可能出现在中间值的左侧 
          else: 
              high = mid - 1
      return find
  

  alist = [1,2,3,4,5,6,7]
  print(middle(alist,5))
  

2. 排序算法

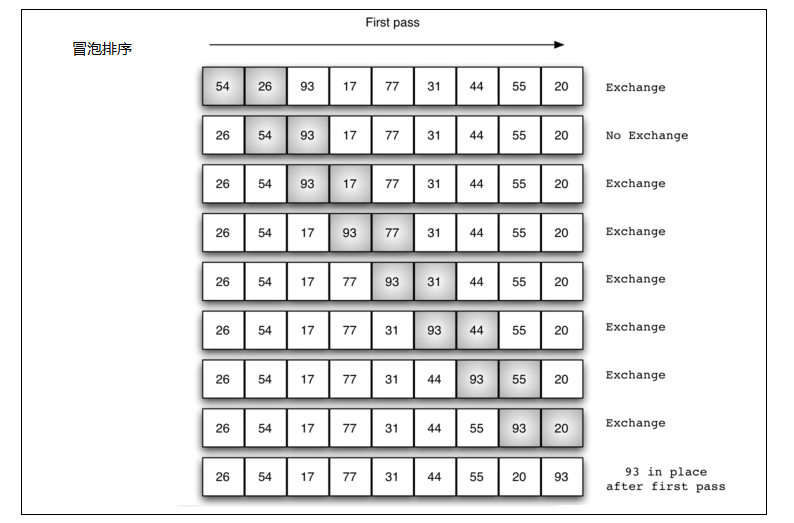
• 冒泡排序

  将乱序列表中的最大值逐步找出，将最大值最终移动到最后的位置

  1.实现将最大的数移到最右边

  def sort(alist):
      for i in range(0,len(alist)-1):  # 循环n-1次，n就是列表元素的个数
          if alist[i] > alist[i+1]:
              alist[i],alist[i+1] = alist[i+1],alist[i]
      print(alist)
  

  alist = [3,8,6,7,5]
  sort(alist)
  
  # 结果：[3, 6, 7, 5, 8]
  

  2.实现冒泡排序：将上述操作逐步作用（n-1）次

  def sort(alist):
      for j in range(0,len(alist)-1):
          for i in range(0,len(alist)-1-j):  # 循环n-1次，n就是列表元素的个数
              if alist[i] > alist[i+1]:
                  alist[i],alist[i+1] = alist[i+1],alist[i]
      return alist
  

  alist = [3,8,6,7,5]
  print(sort(alist))
  
  # 结果：[3, 5, 6, 7, 8]
  

  3.时间复杂度：

  • 最优时间复杂度：O(n)
  • 最坏时间复杂度：O(n2)
  • 平均时间复杂度：O(n2)
  • 稳定性：稳定

  

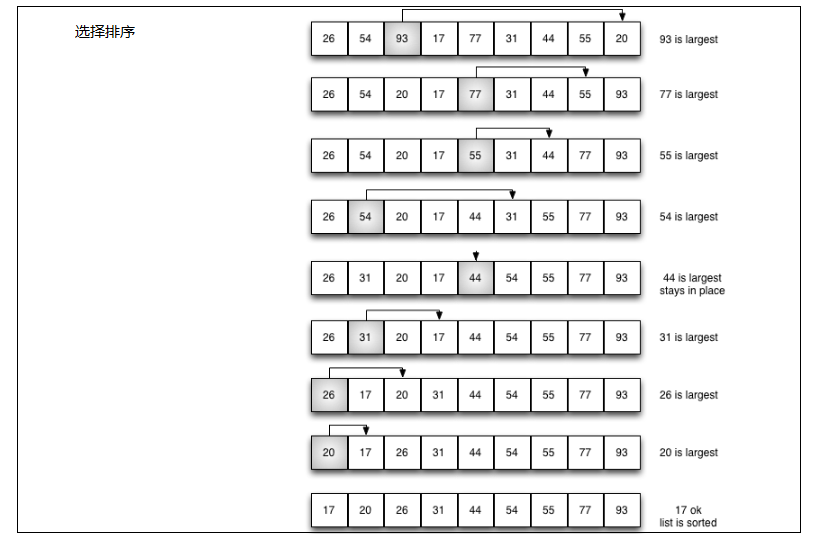
• 选择排序

  直接将列表中最大值找出，直接放置到列表的最后的位置

  1.直接找出列表中的最大值，移到列表最后位置

  def sort(alist):
      max_index = 0  # 最大值的下标，一开始假设第0个元素是最大值
      for i in range(0,len(alist)-1):  # 为了找出最大值的下标
          if alist[max_index] < alist[i+1]:
              max_index = i + 1
      alist[max_index],alist[len(alist)-1] = alist[len(alist)-1],alist[max_index]
      return alist
  

  2.实现选择排序：将上述操作再逐步的作用

  def sort(alist):
      for j in range(0,len(alist)-1):
          max_index = 0  # 最大值的下标，一开始假设第0个元素是最大值
          for i in range(0,len(alist)-1-j):  # 为了找出最大值的下标
              if alist[max_index] < alist[i+1]:
                  max_index = i + 1
          alist[max_index],alist[len(alist)-1-j] = alist[len(alist)-1-j],alist[max_index]
      return alist
  

  alist = [3,8,6,7,5]
  print(sort(alist))
  
  # 结果：[3, 5, 6, 7, 8]
  

  3.时间复杂度：

  • 最优时间复杂度：O(n2)
  • 最坏时间复杂度：O(n2)
  • 平均时间复杂度：O(n2)
  • 稳定性：不稳定

  

• 插入排序

  假设将列表分成两部分，第一部分为列表的第一个元素（有序序列），剩下的元素（无序序列），将无序序列的元素逐一的插入到有序序列的合适位置

  1.有序序列元素只有一个

  # 变量i表示列表下标，还表示有序序列中元素的个数
  # 有序序列只有一个元素，无序序列有n-1个元素
  i = 1  
  # alist[i] 表示的是无需序列的第一个元素
  # alist[i-1]  表示的是有序序列的最后一个元素
  if alist[i] < alist[i-1]:
      alist[i],alist[i-1] = alist[i-1],alist[i]
  

  2.有序序列元素有两个

  i = 2  # 表示有序序列有两个元素
  # alist[i] 表示的是无需序列的第一个元素
  # alist[i-1]  表示的是有序序列的最后一个元素
  while i>1:
      if alist[i] < alist[i-1]:
          alist[i],alist[i-1] = alist[i-1],alist[i]
          i -= 1
      else:
          break
  

  3.实现插入排序：完整代码，自动处理i （len-1）

  def sort(alist):
      for i in range(1,len(alist)):
          while i >= 1:
              if alist[i] < alist[i-1]:
                  alist[i],alist[i-1] = alist[i-1],alist[i]
                  i -= 1
              else:
                  break
      return alist
  

  alist = [49,38,65,97,76,13,27]
  print(sort(alist))
  
  # 结果：[13, 27, 38, 49, 65, 76, 97]
  

  4.时间复杂度：

  • 最优时间复杂度：O(n)
  • 最坏时间复杂度：O(n2)
  • 平均时间复杂度：O(n2)
  • 稳定性：稳定

  

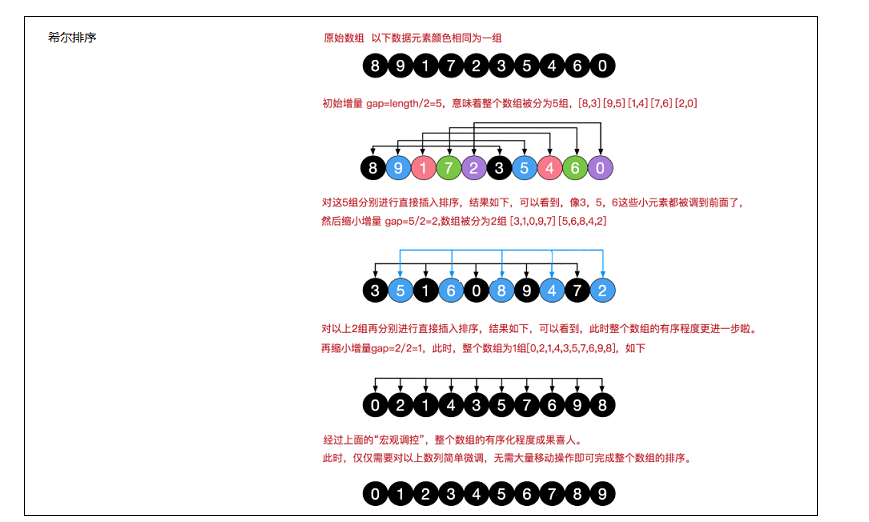
• 希尔排序

  插入排序就是增量为1的希尔排序

  增量（gap）：初始值是元素个数整除2，还可以表示分组的组数（假设）

  1.实现步骤简述

  1.先增量初始值进行分组
  2.每组进行一次插入排序
  3.再缩小增量
  4.再进行每组的插入排序
  5.直到增量为1
  6.最后进行插入排序
  

  2.将插入排序的增量1变成gap

  def sort(alist):
      gap = len(alist)//2
      # 将下属所有的1换成gap
      for i in range(gap,len(alist)):
          while i >= gap:
              if alist[i] < alist[i-gap]:
                  alist[i],alist[i-gap] = alist[i-gap],alist[i]
                  i -= gap
              else:
                  break  
      return alist
  

  3.实现希尔排序：缩减增量

  def sort(alist):
      gap = len(alist)//2
      while gap >= 1:
          # 将下属所有的1换成gap
          for i in range(gap,len(alist)):
              while i >= gap:
                  if alist[i] < alist[i-gap]:
                      alist[i],alist[i-gap] = alist[i-gap],alist[i]
                      i -= gap
                  else:
                      break
          gap //= 2 # 缩减增量            
      return alist
  

  alist = [49,38,65,97,76,13,27]
  print(sort(alist))
  
  # 结果：[13, 27, 38, 49, 65, 76, 97]
  

  5.时间复杂度：

  • 最优时间复杂度：O(n1.3)
  • 最坏时间复杂度：O(n2)
  • 平均时间复杂度：O(nlogn)
  • 稳定性：不稳定

  

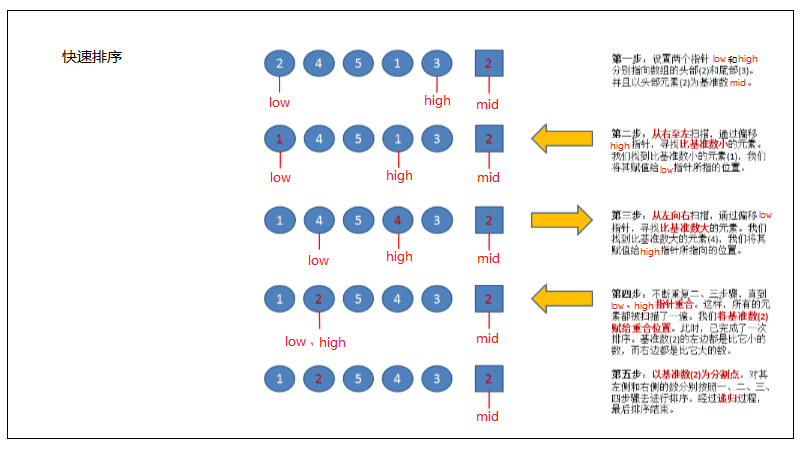
• 快速排序

  有点类似二分查找

  基数：初始值就是列表中的第一个元素

  操作：将整个列表元素中比基数小的值全部放置到基数的左侧，将比基数大的放到基数的右侧

  定义两个变量：
  low ：第0个元素的下标
  high：最后一个元素下标

  1.实现快速排序

  def sort(alist,start,end):
      low = start
      high = end
      if low > high:   # 结束递归的条件
          return
      
      mid = alist[low]  # 基数
      while low < high:
          while low < high:
              if alist[high] > mid:
                  high -= 1  # high向左偏移
              else:
                  alist[low] = alist[high]
                  break
          while low < high:
              if alist[low] < mid:
                  low += 1
              else:
                  alist[high] = alist[low]
                  break
      if low == high:
          alist[low] = mid
      sort(alist,start,high-1)  # 处理基数左部分的乱序序列
      sort(alist,low+1,end)  # 处理基数右部分的乱序序列
      return alist
  

  alist = [49,38,65,97,76,13,27]
  print(sort(alist,0,len(alist)-1))
  
  # 结果：[13, 27, 38, 49, 65, 76, 97]
  

  2.时间复杂度：

  • 最优时间复杂度：O(nlogn)
  • 最坏时间复杂度：O(n2)
  • 平均时间复杂度：O(nlogn)
  • 稳定性：不稳定

  

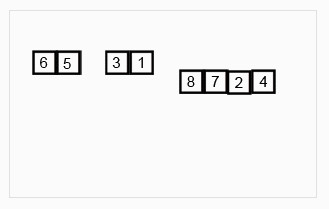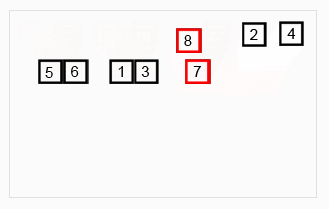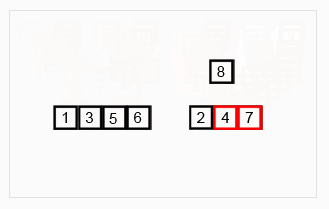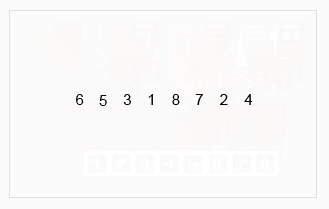
• 归并排序

  归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。

  将数组分解最小之后，然后合并两个有序数组，基本思路就是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另外一个数组的剩余部分复制过来即可。

  归并排序相对于别的排序算法比较浪费空间，因为是重新生成了一个新的空间。

  1.代码实现归并排序：

  def merge_sort(alist):
      """ 归并排序 """
      n = len(alist)
      if n <= 1:
          return alist
      mid = n//2
      # left 采用归并排序后形成的有序的新的列表
      left_li = merge_sort(alist[:mid])
      # right 采用归并排序后形成的有序的新的列表
      right_li = merge_sort(alist[mid:])
      
      # 将两个有序的子序列合并为一个新的整体
      # merge(left,right)
      left_pointer, right_pointer = 0,0
      result = []
      while left_pointer<len(left_li) and right_pointer<len(right_li):
          if left_li[left_pointer] < right_li[right_pointer]:
              result.append(left_li[left_pointer])
              left_pointer += 1
          else:
              result.append(right_li[right_pointer])
              right_pointer += 1
      result += left_li[left_pointer:]
      result += right_li[right_pointer:]
      return result
  

  2.时间复杂度：

  • 最优时间复杂度：O(nlogn)
  • 最坏时间复杂度：O(nlogn)
  • 平均时间复杂度：O(nlogn)
  • 稳定性：稳定

  

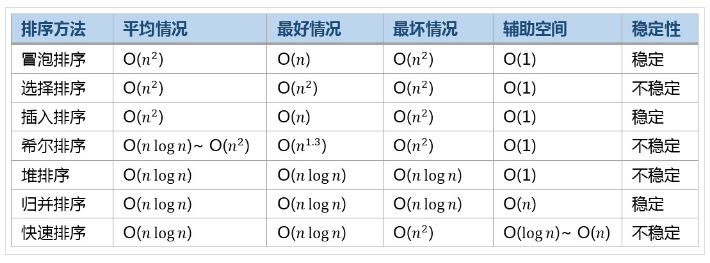
3.排序算法总结