2020牛客NOIP赛前集训营-提高组（第一场）

A 牛牛的方程式

更好的阅读体验

Statement

牛牛最近对三元一次方程非常感兴趣。众所周知，三元一次方程至少需要三个方程组成一个方程组，才有可能得出一组解。

牛牛现在想要知道对于方程 $ax+by+cz=d$ 中有没有至少存在一组 $\{x,y,z\}$ 的解，且 $x,y,z$ 都为整数，使得方程式成立。

裴蜀定理

对于方程 $ax+by=z$ ，当且仅当 $\gcd(a,b)|z$ 时方程有整数解。

题解

容易将上述定理拓展到多元情况。

当 $\gcd\{a,b,c\}|z$ 时，有整数解。

但是当 $a=b=c=0$ 时，方程存在两种情况：

$\begin{cases} z=0 & (1) \\ z \neq 0 & (2) \end{cases}$

对于 $(1)$ 式， $x,y,z \in \mathbb{Z}$ ，对于 $(2)$ 式， $x,y,z$ 无解。

如果不对 $a = b=c=0$ 进行特判，会因为浮点错误 RE 掉 50 分。

代码

 #include<bits/stdc++.h>
using namespace std;
 
#define int long long
 
template < typename Tp >
inline void read(Tp &x) {
	x = 0; int fh = 1; char ch = 1;
	while(ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
	if(ch == '-') fh = -1, ch = getchar();
	while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
	x *= fh;
}
 
template < typename Tp >
inline void biread(Tp &x) {
	x = 0; int fh = 1; char ch = 1;
	while(ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
	if(ch == '-') fh = -1, ch = getchar();
	while(ch >= '0' && ch <= '9') x = x * 2 + ch - '0', ch = getchar();
	x *= fh;
}
 
int T;
int a, b, c, d;
 
inline void Init(void) {
	read(T);
}
 
inline void Work(void) {
	while(T--) {
		read(a); read(b); read(c); read(d);
		if(a == b && b == c && c == 0) {
			if(d == 0) puts("YES");
			else puts("NO");
			continue;
		} 
		int p = __gcd(a, __gcd(b, c));
		if(d % p == 0) puts("YES");
		else puts("NO");
	}
}
 
signed main(void) {
	Init();
	Work();
	return 0;
}

B 牛牛的猜球游戏

更好的阅读体验

Statement

牛牛和牛妹在玩猜球游戏,牛牛首先准备了 $10$ 个小球，小球的编号从 $0 - 9$ 。首先牛牛把这 $10$ 个球按照从左到右编号为 $0,1,2,3 \cdots 9$ 的顺序摆在了桌子上，接下来牛牛把这 $10$ 个球用 $10$ 个不透明的杯子倒扣住。

牛牛接下来会按照一定的操作顺序以极快的速度交换这些杯子。

换完以后他问牛妹你看清楚从左到右的杯子中小球的编号了么？

由于牛妹的动态视力不是很好，所以她跑来向你求助。你在调查后发现牛牛置换杯子其实是有一定原则的。

具体来讲，牛牛有一个长度大小为 $n$ 的操作序列。

操作序列的每一行表示一次操作都有两个非负整数 $a,b$ ，表示本次操作将会交换从左往右数第 $a$ 个杯子和从左往右数第 $b$ 个杯子（ $a$ 和 $b$ 均从 $0$ 开始数）。请注意是换杯子，而不是直接交换 $a$ 号球和 $b$ 号球

牛牛和牛妹一共玩了 $m$ 次猜球游戏，在每一轮游戏开始时，他都将杯子中的小球重置到从左往右依次为 $0,1,2,3 \cdots 9$ 的状态。

然后在第 $i$ 轮游戏中牛牛会按照操作序列中的第 $l_i$ 个操作开始做，一直做到第 $r_i$ 个操作结束（ $l$ 和 $r$ 的编号从 1 开始计算）。

由于你提前搞到了牛牛的操作序列以及每一次游戏的 $l,r$ 。请你帮助牛妹回答出牛牛每一轮游戏结束时，从左至右的杯子中小球的编号各是多少。

题解 $1$ - 线段树 $O((n + T) \log n)$

对于区间 $[l,r]$ ，维护执行编号在 $[l,r]$ 的操作的答案。

考虑如何合并左右子树答案。

实际上，假设右子树答案为 $r_0,r_1,r_2,r_3,r_4,r_5,r_6,r_7,r_8,r_9$

左子树答案为 $l_0,l_1,l_2,l_3,l_4,l_5,l_6,l_7,l_8,l_9$

考虑杯子编号，实际上，由于每一个询问，都是将杯子按照 $0,1,2, \cdots, 9$ 的初始状态排列的，可以将杯子编号看作是杯子的相对位置。

将左子树对应位置的杯子按照右子树序列移动一下即可。

这实际上是一个序列置换，序列置换具有结合律，这也决定了应用线段树必须具有的区间可加性。

题解 $2$ - 预处理 $O(n + T)$

同上解法一，因为序列置换具有的结合律，实际上先 $O(n)$ 模拟一遍并记录答案即可，并不需要线段树。

线段树代码

 #include<bits/stdc++.h>
using namespace std;
 
template < typename Tp >
inline void read(Tp &x) {
	x = 0; int fh = 1; char ch = 1;
	while(ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
	if(ch == '-') fh = -1, ch = getchar();
	while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
	x *= fh;
}
 
template < typename Tp >
inline void biread(Tp &x) {
	x = 0; int fh = 1; char ch = 1;
	while(ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
	if(ch == '-') fh = -1, ch = getchar();
	while(ch >= '0' && ch <= '9') x = x * 2 + ch - '0', ch = getchar();
	x *= fh;
}
 
const int maxn = 100000 + 7;
 
int n, T;
int val[maxn * 4][10];
 
#define lfc (x << 1)
#define rgc ((x << 1) | 1)
int cp[10];
void build(int x, int l, int r) {
	if(l == r) {
		int p, q;
		read(p); read(q);
		val[x][0] = 0, val[x][1] = 1, val[x][2] = 2, val[x][3] = 3, val[x][4] = 4, val[x][5] = 5, val[x][6] = 6, val[x][7] = 7, val[x][8] = 8, val[x][9] = 9;
		swap(val[x][p], val[x][q]);
		return ;
	}
	int mid = (l + r) >> 1;
	build(lfc, l, mid); build(rgc, mid + 1, r);
	for(int i = 0; i < 10; i++) {
		val[x][i] = val[lfc][val[rgc][i]];
	}
}
 
int ans[10];
 
void query(int x, int l, int r, int L, int R) {
	if(L <= l && r <= R) {
		memcpy(cp, ans, sizeof(ans));
		for(int i = 0; i < 10; i++) {
			ans[i] = cp[val[x][i]];
		}
		return ;
	}
	if(r < L || R < l) return ;
	int mid = (l + r) >> 1;
	query(lfc, l, mid, L, R); query(rgc, mid + 1, r, L, R);
}
 
inline void Init(void) {
	read(n); read(T);
}
 
inline void Work(void) {
	build(1, 1, n); // check done
	while(T--) {
		int l, r; read(l); read(r);
		ans[0] = 0, ans[1] = 1, ans[2] = 2, ans[3] = 3, ans[4] = 4, ans[5] = 5, ans[6] = 6, ans[7] = 7, ans[8] = 8, ans[9] = 9;
		query(1, 1, n, l, r);
		for(int i = 0; i <= 9; i++) printf("%d%c", ans[i], " \n"[i == 9]);
	}
}
 
signed main(void) {
//	freopen("B.in", "r", stdin);
//	freopen("test.out", "w", stdout); 
	Init();
	Work();
	return 0;
}

C 牛牛的凑数游戏

更好的阅读体验

Statement

对于一个多重数集 $\{S\}$ ，对于一非负整数 $x$ ，若存在 $S' \subseteq S$ 且 $\{S'\}$ 中所有数字之和恰好等于 $x$ ，则说 $\{S\}$ 可以表示 $x$ 。

显然对于任意的多重数集都可以表示 $0$ ，因为空集是所有集合的子集。

牛牛定义集合 $\{S\}$ 的最小不能表示数为，一个最小的非负整数 $x$ ， $\{S\}$ 不能表示 $x$ 。

举个例子来说，例如 $S=\{1,2,3,8,9\}$ ，那么集合 $\{S\}$ 的最小不能表示数就为 $7$ 。

因为子集 $\varnothing$ 的和为 $0$ ，子集 $\{1\}$ 的和为 $1$ ，子集 $\{2\}$ 的和为 $2$ ，子集 $\{1,2\}$ 的和为 $3$ ，子集 $\{1,3\}$ 的和为 $4$ ，子集 $\{2,3\}$ 的和为 $5$ ，子集 $\{1,2,3\}$ 的和为 $6$ 。

但是无法找到子集权值和恰好为 $7$ 的子集，所以 $7$ 无法表示。

现在有一个长度大小为 $n$ 的正整数数组，牛牛每次选择一个区间 $[l,r]$ ，他想要知道假定给出的多重数集为 $\{a_l,a_{l+1}...a_{r}\}$ 时，该集合的最小不能表示数是多少。

多重数集最小不可表示数

Theorem 设多重数集 $S$ ，将 $S$ 中的数从小到大排列，其中第 $i$ 小的数为 $a_i$ ，记 $s_i = \sum_{i=1}^{n}{a_i}$ 当 $s_i < a_{i+1} - 1$ 时集合 $S$ 的最小不可表示数为 $s_i+1$

Prove

先证充分性。

$s_i + 1$ 只能由 $a_1, a_2, \cdots, a_i$ 加和得到，但 $a_1 + a_2 + \cdots + a_i = s_i < s_i + 1$ 。

题解

迭代，主席树维护。

代码

D 牛牛的RPG游戏

更好的阅读体验

Statement

牛牛最近在玩一款叫做“地牢迷宫”的游戏，该游戏中的每一层都可以看成是一个的二维棋盘，牛牛从左上角起始的点移动到右下角的 $(n,m)$ 点。

游戏中的每一个格子都会触发一些事件，这些事件将会影响玩家的得分。

具体来说，每到一个格子玩家触发事件时，首先会立即获得一个收益得分 $val(i,j)$ 。注意这个得分不一定是正的，当它的值为负时将会扣除玩家一定的分数。

同时这个事件还会对玩家造成持续的影响，直到玩家下一次触发其他事件为止，每走一步，玩家都会获得上一个事件触发点 $buff(i,j)$ 的得分。

在游戏开始时牛牛身上还没有任何的 $buff$ ，所以在牛牛还未触发任何事件之前每走一步都不会产生任何影响。

牛牛使用“潜行者”这个职业，所以他路过地牢中的格子时，可以选择不去触发这些事件。

同时牛牛是一个速通玩家，想要快速的到达终点，所以他每次只会选择往右走或者往下走。

牛牛想要知道，他玩游戏可以获得的最大得分是多少，你能告诉他么。

CDQ 分治及其在 DP 方面的应用

可以参见本场出题人神仙的博客 https://blog.nowcoder.net/n/f44d4aada5a24f619442dd6ddffa7320

CDQ 主要能够对偏序形式限制的 DP 转移顺序，直接拍掉一维

题解

设 $dp(i,j)$ 代表到 $(i,j)$ 且触发其事件的最大收益。

因为终点的 $buff$ 和 $val$ 都为 $0$ ，所以上述状态是正确的。

容易写出转移方程 $dp(i,j) = \max \{ dp(x,y) + ((i + j) - (x + y)) \times buff_{x,y} + val_{i,j} \}$

且要求满足 $\begin{cases} x \le i & (1)\\ y \le j & (2) \end{cases}$ 两个限制条件

发现转移方程符合斜率优化形式，扒掉 $\max$ 并变形后得到 $\begin{matrix}\underbrace{dp(x,y)-(x+y) \times buff_{x,y}}\\y\end{matrix}=\begin{matrix}\underbrace{-(i+j)}\\k\end{matrix} \times \begin{matrix}\underbrace{buff_{x,y}}\\x\end{matrix}+\begin{matrix}\underbrace{val(i,j)+dp(i,j)}\\b\end{matrix}$

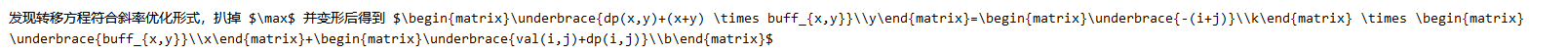
公式打吐了

注意到转移顺序非常毒瘤，需要使用 cdq 分治将 $x \le i$ 的限制条件直接拍扁。

又注意到 $\begin{matrix}\underbrace{-(i+j)}\\k\end{matrix}$ 和 $\begin{matrix}\underbrace{buff_{x,y}}\\x\end{matrix}$ 不满足单调增，转移需要 cdq 分治 / 二分 / 李超线段树。

用命题人的话来说，算法 + 数据结构非常优美，我选李超树。

李超树用的 dp 式子就是上面那个暴力式子，而不是后面的斜率柿子，这也是考试时候 40 -> 10 的原因。

李超树形式的式子： $\begin{matrix}\underbrace{dp(i,j)-val_{i,j}}\\y\end{matrix}=\begin{matrix}\underbrace{buff_{x,y}}\\k\end{matrix} \times \begin{matrix}\underbrace{(i+j)}\\x\end{matrix}\begin{matrix}\underbrace{-(x+y) \times buff_{x,y} + dp(x,y)}\\b\end{matrix}$

代码

 #include<bits/stdc++.h>
using namespace std;
 
#define int long long
 
template < typename Tp >
inline void read(Tp &x) {
	x = 0; int fh = 1; char ch = 1;
	while(ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
	if(ch == '-') fh = -1, ch = getchar();
	while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
	x *= fh;
}
 
template < typename Tp >
inline void biread(Tp &x) {
	x = 0; int fh = 1; char ch = 1;
	while(ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
	if(ch == '-') fh = -1, ch = getchar();
	while(ch >= '0' && ch <= '9') x = x * 2 + ch - '0', ch = getchar();
	x *= fh;
}
 
const int maxn = 500000 + 7;
 
int n, m;
int buff[maxn], v[maxn];
 
struct Interval {
	int id;
	int k, b;
}val[5000000];
int lfc[5000000], rgc[5000000], cnt;
 
int dp[maxn];
 
inline int id(int x, int y) {
	return (x - 1) * m + y;
}
 
inline void reserv(int k, int &x ,int &y) {
	x = k / m + 1, y = k % m;
	if(y == 0) y = m, x--;
}
 
inline int calc(Interval p, int x) {
	return p.k * x + p.b;
}
 
inline int New(){
	++cnt;
	lfc[cnt] = rgc[cnt] = val[cnt].id = val[cnt].k = val[cnt].b = 0;
	return cnt;
}
 
void modify(int x, int l, int r, int L, int R, Interval p) {
	int mid = (l + r) >> 1;
	if(L <= l && r <= R) {
		if(!val[x].id || calc(val[x], mid) < calc(p, mid)) swap(val[x], p);
		if(!p.id || p.k == val[x].k || l == r) return ;
		double cross = (double)(p.b - val[x].b) / (double)(val[x].k - p.k);
		if(cross < (double)l || cross > (double)r) return ;
		if(p.k < val[x].k) {
			if(!lfc[x]) lfc[x] = New();
			modify(lfc[x], l, mid, L, R, p);
		}
		else {
			if(!rgc[x]) rgc[x] = New();
			modify(rgc[x], mid + 1, r, L, R, p);
		}
	}
	else {
		if(L <= mid) {
			if(!lfc[x]) lfc[x] = New();
			modify(lfc[x], l, mid, L, R, p);
		}
		if(R > mid) {
			if(!rgc[x]) rgc[x] = New();
			modify(rgc[x], mid + 1, r, L, R, p);
		}
	}
}
 
Interval query(int x, int l, int r, int pos) {
	if(l == r) return val[x];
	int mid = (l + r) >> 1;
	Interval res;
	if(pos <= mid) {
		if(!lfc[x]) lfc[x] = New();
		res = query(lfc[x], l, mid, pos);
	}
	else {
		if(!rgc[x]) rgc[x] = New();
		res = query(rgc[x], mid + 1, r, pos);
	}
	if(!res.id || calc(res, pos) < calc(val[x], pos)) return val[x];
	return res;
}
 
void cdq(int l, int r) {
	if(l == r) {
		cnt = 0; New();// val[1].b = -0x3f3f3f3f3f3f3f3fll;
		Interval q;
//		if(l == 1) 
		q.id = id(l, 1), q.k = buff[id(l, 1)], q.b = dp[id(l, 1)] - (l + 1) * buff[id(l, 1)];
		modify(1, 1, m + n, 1, m + n, q);
		for(int i = 2; i <= m; i++) {
			Interval p = query(1, 1, n + m, (l + i));
			int k = p.id, x, y; reserv(k, x, y);
			dp[id(l, i)] = max(dp[id(l, i)], dp[k] + (l + i - x - y) * buff[k] + v[id(l, i)]);
			p.id = id(l, i), p.k = buff[id(l, i)], p.b = dp[id(l, i)] - (l + i) * buff[id(l, i)];
			modify(1, 1, n + m, 1, n + m, p);
		}
		return ;
	}
	int mid = (l + r) >> 1;
	cdq(l, mid);
	cnt = 0; New();// val[1].b = -0x3f3f3f3f3f3f3f3fll;
	for(int j = 1; j <= m; j++) {
		for(int i = l; i <= mid; i++) {
			Interval p; p.id = id(i, j), p.k = buff[id(i, j)], p.b = dp[id(i, j)] - (i + j) * buff[id(i, j)];
			modify(1, 1, n + m, 1, n + m, p);
		}
		for(int i = mid + 1; i <= r; i++) {
			Interval p = query(1, 1, n + m, i + j);
			int k = p.id, x, y; reserv(k, x, y);
			dp[id(i, j)] = max(dp[id(i, j)], dp[k] + (i + j - x - y) * buff[k] + v[id(i, j)]);
			p.id = id(i, j), p.k = buff[id(i, j)], p.b = dp[id(i, j)] - (i + j) * buff[id(i, j)];
//			modify(1, 1, n + m, 1, n + m, p);
		}
	}
	cdq(mid + 1, r);
}
 
inline void Init(void) {
	read(n); read(m);
//	for(int i = 1; i <= id())
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			read(buff[id(i, j)]);
			dp[id(i, j)] = -0x3f3f3f3f3f3f3f3fll;
		}
	}
	dp[1] = 0;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			read(v[id(i, j)]);
		}
	}
}
 
inline void Work(void) {
	cdq(1, n);
	printf("%lld\n", dp[id(n, m)]);
}
 
signed main(void) {
	Init();
	Work();
	return 0;
}

posted @ 2020-10-20 17:36 览遍千秋阅读(598) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 使用C#创建一个MCP客户端
· ollama系列1：轻松3步本地部署deepseek，普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· 按钮权限的设计及实现

历史上的今天：
2019-10-20 CSP2019-S1 游记

公告

昵称：览遍千秋
园龄： 5年6个月
粉丝： 32
关注： 14

+加关注

2025年3月

日

一

二

三

四

五

六

览遍千秋

在鲜血流尽之前，请用燧石划过刀锋，留下一盏小小的灯

2020牛客NOIP赛前集训营-提高组（第一场）

A 牛牛的方程式

Statement

裴蜀定理

题解

代码

B 牛牛的猜球游戏

Statement

题解 $1$ - 线段树 $O((n + T) \log n)$

题解 $2$ - 预处理 $O(n + T)$

线段树代码

C 牛牛的凑数游戏

Statement

多重数集最小不可表示数

题解

代码

D 牛牛的RPG游戏

Statement

CDQ 分治及其在 DP 方面的应用

题解

代码

公告

搜索

常用链接

随笔分类 (214)

随笔档案 (156)

膜拜对象

神仙学长们

同是追梦人

同在江苏

阅读排行榜

评论排行榜

推荐排行榜

最新评论

	#include<bits/stdc++.h>
	using namespace std;

	#define int long long

	template < typename Tp >
	inline void read(Tp &x) {
	x = 0; int fh = 1; char ch = 1;
	while(ch != '-' && (ch < '0' \|\| ch > '9')) ch = getchar();
	if(ch == '-') fh = -1, ch = getchar();
	while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
	x *= fh;
	}

	template < typename Tp >
	inline void biread(Tp &x) {
	x = 0; int fh = 1; char ch = 1;
	while(ch != '-' && (ch < '0' \|\| ch > '9')) ch = getchar();
	if(ch == '-') fh = -1, ch = getchar();
	while(ch >= '0' && ch <= '9') x = x * 2 + ch - '0', ch = getchar();
	x *= fh;
	}

	int T;
	int a, b, c, d;

	inline void Init(void) {
	read(T);
	}

	inline void Work(void) {
	while(T--) {
	read(a); read(b); read(c); read(d);
	if(a == b && b == c && c == 0) {
	if(d == 0) puts("YES");
	else puts("NO");
	continue;
	}
	int p = __gcd(a, __gcd(b, c));
	if(d % p == 0) puts("YES");
	else puts("NO");
	}
	}

	signed main(void) {
	Init();
	Work();
	return 0;
	}

览遍千秋

在鲜血流尽之前，请用燧石划过刀锋，留下一盏小小的灯

2020牛客NOIP赛前集训营-提高组（第一场）

A 牛牛的方程式

Statement

裴蜀定理

题解

代码

B 牛牛的猜球游戏

Statement

题解 111 - 线段树 O((n+T)logn)O((n+T)log⁡n)O((n + T) \log n)

题解 222 - 预处理 O(n+T)O(n+T)O(n + T)

线段树代码

C 牛牛的凑数游戏

Statement

多重数集最小不可表示数

题解

代码

D 牛牛的RPG游戏

Statement

CDQ 分治及其在 DP 方面的应用

题解

代码

公告

搜索

常用链接

随笔分类 (214)

随笔档案 (156)

膜拜对象

神仙学长们

同是追梦人

同在江苏

阅读排行榜

评论排行榜

推荐排行榜

最新评论

题解 $1$ - 线段树 $O((n + T) \log n)$

题解 $2$ - 预处理 $O(n + T)$