CF337D Book of Evil 换根树形DP
稍微复杂的换根 DP,我能一发 A 掉的还是不多的...
题目大意
给出一棵有 \(n\) 个结点的树,其中 \(m\) 个结点 \(p_1,p_2,\cdots,p_m\) 作特殊标记,令 \(dis(x,y)\) 代表结点 \(x\) 到 \(y\) 简单路径上边数,求有多少个点 \(x\) ,满足 \(\forall i \in [1,m] ,\max\{dis(x,p_i)\} \le d\)
题解
不妨令 \(1\) 为根。
考虑结点 \(x\) 的最远标记点,可以在 \(x\) 的子树 \(T(x)\) 内,也可以在 \(x\) 的子树外。
对这两种情况分别讨论。
\(\texttt{Part I}\)
在 \(x\) 的子树内情况比较简单,可以通过一次 dfs 求出。
记 \(dp(x)\) 为 \(T(x)\) 内最远标记点到 \(x\) 的距离,如果 \(T(x)\) 内没有标记点,则 \(dp(x) = +\infty\)
但在这个 dfs 过程中,还要维护\(T(x)\) 内第二远标记点到 \(x\) 的距离 \(dp2(x)\),原因将在 \(\texttt{Part II}\) 解释。
\(\texttt{Part II}\)
在 \(x\) 的子树外情况比较复杂,但可以自然地想到是一个换根 DP:根 \(1\) 号点不存在子树外情况,已经可以求解。
假设 \(y\) 是 \(x\) 的任一儿子,此时对 \(y\) 有两种情况:
- \(dp(x) = dp(y) + 1\) ,即 \(dp(x)\) 由 \(dp(y)\) 转移而来
- \(dp(x) \neq dp(y) + 1\) ,即 \(dp(x)\) 不是由 \(dp(y)\) 转移而来。
以题目样例为例
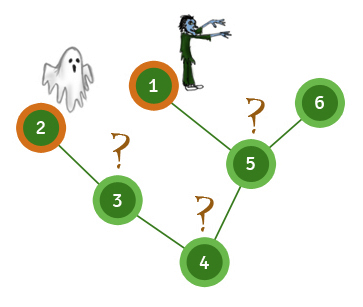
其中 \(1\) 号点只有一个儿子 \(5\) 号点,那么 \(5\) 号点符合上述的第一种情况,也就是说,\(1\) 号点的最远点就在孩子 \(5\) 号子树内。
此时,如果从 \(1\) 号点向 \(5\) 号点换根,如果使用 \(dp(1)\),则 \(5\) 号点子树外的情况并未得到考虑,所以还需要记录 \(\texttt{Part I}\) 中所述的 \(dp2(x)\) ,并在换根过程中分类讨论。
其他细节请见代码。
\(\texttt{Code}\)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
template < typename Tp >
void read(Tp &x) {
x = 0; int fh = 1; char ch = 1;
while(ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if(ch == '-') fh = -1, ch = getchar();
while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
x *= fh;
}
const int maxn = 100000 + 7;
const int maxm = 200000 + 7;
const int INF = 0x3f3f3f3f;
int n, m, d, dp[maxn], dp2[maxn];
bool mark[maxn];
int Head[maxn], Next[maxm], to[maxm], tot;
void addedge(int x, int y) {
to[++tot] = y, Next[tot] = Head[x], Head[x] = tot;
}
void add(int x, int y){
addedge(x, y); addedge(y, x);
}
void Init(void) {
read(n); read(m); read(d);
for(int i = 1, x; i <= m; i++) {
read(x); mark[x] = true;
}
for(int i = 1, x, y; i < n; i++) {
read(x); read(y);
add(x, y);
}
}
void dfs(int x, int fa) {
dp[x] = dp2[x] = INF;
for(int i = Head[x] ;i ; i = Next[i]) {
int y = to[i];
if(y == fa) continue;
dfs(y, x);
if(dp[y] != INF) {
if(dp[x] == INF) dp[x] = dp[y] + 1;
else {
if(dp[y] + 1 > dp[x]) {
dp2[x] = dp[x];
dp[x] = dp[y] + 1;
}
else if(dp2[x] == INF) dp2[x] = dp[y] + 1;
else dp2[x] = max(dp2[x], dp[y] + 1);
}
}
}
if(dp[x] == INF) if(mark[x]) dp[x] = 0;
}
int ans;
void dfs2(int x, int fa, int mov) {
if(mov == INF && mark[fa]) mov = 1;
// printf("id = %d, fa = %d, mov = %d, dp[x] = %d\n", x, fa, mov, dp[x]);
if((dp[x] <= d || dp[x] == INF) && (mov <= d || mov == INF)) {
++ans;
}
for(int i = Head[x]; i; i = Next[i]) {
int y = to[i];
if(y == fa) continue;
if(dp[x] == dp[y] + 1) {
if(mov == INF && dp2[x] != INF) dfs2(y, x, dp2[x] + 1);
else if(mov != INF && dp2[x] == INF) dfs2(y, x, mov + 1);
else if(mov == INF && dp2[x] == INF) dfs2(y, x, INF);
else dfs2(y, x, max(dp2[x], mov) + 1);
}
else {
if(mov == INF && dp[x] != INF) dfs2(y, x, dp[x] + 1);
else if(mov != INF && dp[x] == INF) dfs2(y, x, mov + 1);
else if(mov == INF && dp[x] == INF) dfs2(y, x, INF);
else dfs2(y, x, max(dp[x], mov) + 1);
}
}
}
void Work(void) {
dfs(1, 0);
// for(int i = 1; i <= n; i++) {
// printf("%d : %d\n", i, dp[i]);
// }
dfs2(1, 0, INF);
printf("%d\n", ans);
}
int main(void) {
Init();
Work();
return 0;
}


