牛客OI周赛14 普及组
Prologue
菜的真实,普及都 AK 不掉..
Score: 100 + 100 + 100 + 0 = 300
rank: 16
A String
看来 PJ T1 考字符串读入成铁上钉钉了?
考虑开桶 \(a\) ,记录 ASCII 为 \(i\) 的字符是否出现即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 100000 + 7;
const int maxm = 200000 + 7;
int n, m;
#ifdef Graph_Define
int Head[maxn], to[maxm], Next[maxm], tot;
void addedge(int x, int y) {
to[++tot] = y, Next[tot] = Head[x], Head[x] = tot;
}
void add(int x, int y) {
addedge(x, y);
addedge(y, x);
}
#endif
template < typename Tp >
void read(Tp &x) {
x = 0;char ch = 1;int fh = 1;
while(ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if(ch == '-') fh = -1, ch=getchar();
while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
x *= fh;
}
string s;
bool a[200];
void Init(void) {
cin >> s;
}
int ans;
void Work(void) {
for(int i = 0; i < (int)s.size(); i++) {
if(!a[s[i]]) ++ans;
a[s[i]] = 1;
}
cout << ans << '\n';
}
int main() {
Init();
Work();
return 0;
}
B Number
发现 \(a_i \le 10^9\) ,考虑到 \(2^{22} >> 10^9\) ,所以对这些数暴力分解,枚举到其 \(22\) 次方的和即可。
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long LL;
const int maxn = 100000 + 7;
const int maxm = 200000 + 7;
int n, m;
#ifdef Graph_Define
int Head[maxn], to[maxm], Next[maxm], tot;
void addedge(int x, int y) {
to[++tot] = y, Next[tot] = Head[x], Head[x] = tot;
}
void add(int x, int y) {
addedge(x, y);
addedge(y, x);
}
#endif
template < typename Tp >
void read(Tp &x) {
x = 0;char ch = 1;int fh = 1;
while(ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if(ch == '-') fh = -1, ch=getchar();
while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
x *= fh;
}
int T;
void Init(void) {
read(T);
}
int ans;
int fpow(int x, int p) {
int res = 1;
while(p) {
if(p & 1) res = res * x;
p >>= 1, x = x * x;
}
return res;
}
bool check(int x) {
vector < int > v;
int copy = x;
while(copy) {
v.push_back(copy % 10);
copy /= 10;
}
int k = (int)v.size();
int times = 0;
while(copy < x && times <= 22) {
copy = 0;
for(auto i : v) {
copy += fpow(i,times);
if(copy > x) return false;
}
if(copy == x) return true;
if(copy > x) return false;
++times;
}
return false;
}
void Work(void) {
while(T--) {
read(n);
if(check(n)) ++ans;
}
printf("%lld\n", ans);
}
signed main() {
Init();
Work();
return 0;
}
C Tree
换根树形 DP。
先钦定 \(1\) 为根,把 dep 都跑出来。
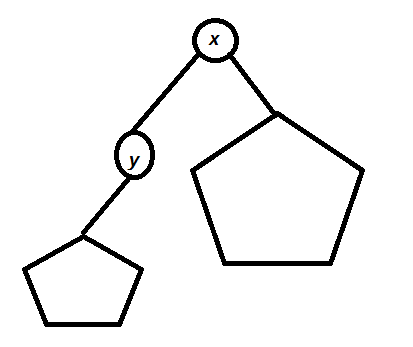
假设当前 \(x\) 为根,向 \(y\) 换根时,有 \(n - size_y\) 的点距离增加一,有 \(size_y\) 个点距离减少一。
所以搜一遍就出来了。
另外,看到有人写了一个树的重心 A 掉了,不是很理解。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 1000000 + 7;
const int maxm = 2000000 + 7;
const int INF = 0x3f3f3f3f;
int n, m;
#define Graph_Define
#ifdef Graph_Define
int Head[maxn], to[maxm], Next[maxm], tot;
void addedge(int x, int y) {
to[++tot] = y, Next[tot] = Head[x], Head[x] = tot;
}
void add(int x, int y) {
addedge(x, y);
addedge(y, x);
}
#endif
template < typename Tp >
void read(Tp &x) {
x = 0;char ch = 1;int fh = 1;
while(ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if(ch == '-') fh = -1, ch=getchar();
while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
x *= fh;
}
void Init(void) {
read(n);
for(int i = 1, x, y; i < n; i++) {
read(x); read(y);
add(x, y);
}
}
int dep[maxn], size[maxn], sum[maxn];
void dfs1(int x, int f, int dp) {
size[x] = 1, dep[x] = dp, sum[x] += dp;
for(int i = Head[x]; i; i = Next[i]) {
int y = to[i];
if(y == f) continue;
dfs1(y, x, dp + 1);
size[x] += size[y], sum[x] += sum[y];
}
}
int ans = INF;
void dfs2(int x, int f, int val) {
ans = min(ans, val);
for(int i = Head[x]; i; i = Next[i]) {
int y = to[i];
if(y == f) continue;
dfs2(y, x, val + n - size[y] - size[y]);
}
}
void Work(void) {
dfs1(1, 0, 0);
dfs2(1, 0, sum[1]);
printf("%d\n", ans);
}
int main() {
Init();
Work();
return 0;
}
D Talk
不会,好神仙的题啊,在此膜拜切掉的那群神仙。
官方题解:


所以为啥不把数据范围开大点出个矩阵快速幂啊...

