20191028 牛客网CSP-S Round2019-1
花了 \(30min\) 打了 \(180\) 分的暴力...
仓鼠的石子游戏
问题描述
链接:https://ac.nowcoder.com/acm/contest/1100/A
仓鼠和兔子被禁止玩电脑,无聊的他们跑到一块空地上,空地上有许多小石子。兔子捡了很多石子,然后将石子摆成n个圈,每个圈由a[i]个石子组成。然后兔子有两根彩色笔,一支红色一支蓝色。兔子和仓鼠轮流选择一个没有上色的石子涂上颜色,兔子每次可以选择一个还未染色的石子将其染成红色,而仓鼠每次可以选择一个还未染色的石子将其染成蓝色,并且仓鼠和兔子约定,轮流染色的过程中不能出现相邻石子同色,谁不能操作他就输了。假设他们两个都使用了最优策略来玩这个游戏,并且兔子先手,最终谁会赢得游戏?
输入格式
第一行输入一个正整数T,表示有T组测试案例。
每组测试案例的第一行输入一个n,表示有n圈石子。 第二行输入n个正整数a[i],表示每个圈的石子数量。
输出格式
对于每组测试案例,如果兔子赢了,输出”rabbit“(不含引号)如果仓鼠赢了,输出"hamster"(不含引号)。
数据规模与约定
本题共有10组测试点数据。
对于前 \(30\%\) 的数据,满足 \(n=1,1 \le a[i] \le 7,1 \le T \le 10\)
对于前 \(60\%\) 的数据,满足 \(1 \le n \le 10^3,1 \le a[i] \le 7,1 \le T \le 10^2\) 。
对于前 \(100\%\) 的数据,满足 \(1 \le n \le 10^3,1 \le a[i] \le 10^9,1 \le T \le 10^2\)。
对于测试点 \(6\) ,在满足前 \(60\%\) 的数据条件下,额外满足 \(a[i]=1\) 。
题解
发现对于每一堆来说:
-
偶数堆相当于没有:不能改变先后手顺序
-
奇数堆:只能放偶数个
-
\(1\)的堆:改变先后手
因此,只保留 \(1\) 个奇数堆。这个奇数堆进入时是先手的人输。
就相当于用 \(1\) 的堆改变先后手后,看谁是后手。
发现当 \(1\) 堆的数目为奇数时, rabbit 赢,否则 hamster 赢。
\(\mathrm{Code}\)
#include<bits/stdc++.h>
using namespace std;
template <typename Tp>
void read(Tp &x){
x=0;char ch=1;int fh;
while(ch!='-'&&(ch>'9'||ch<'0')) ch=getchar();
if(ch=='-') ch=getchar(),fh=-1;
else fh=1;
while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
x*=fh;
}
const int maxn=1007;
int T,n,sum;
int a[maxn];
int cnt;
void reset(){
sum=cnt=0;
}
int main(){
read(T);
while(T--){
read(n);reset();
for(int i=1;i<=n;i++){
read(a[i]);
if(a[i]==1) ++sum;
else if(a[i]&1) ++cnt;
}
cnt=cnt%2;
if(cnt==0){
if(sum&1) puts("rabbit");
else puts("hamster");
}
else{
if(sum&1) puts("rabbit");
else puts("hamster");
}
}
return 0;
}
乃爱与城市的拥挤程度
问题描述

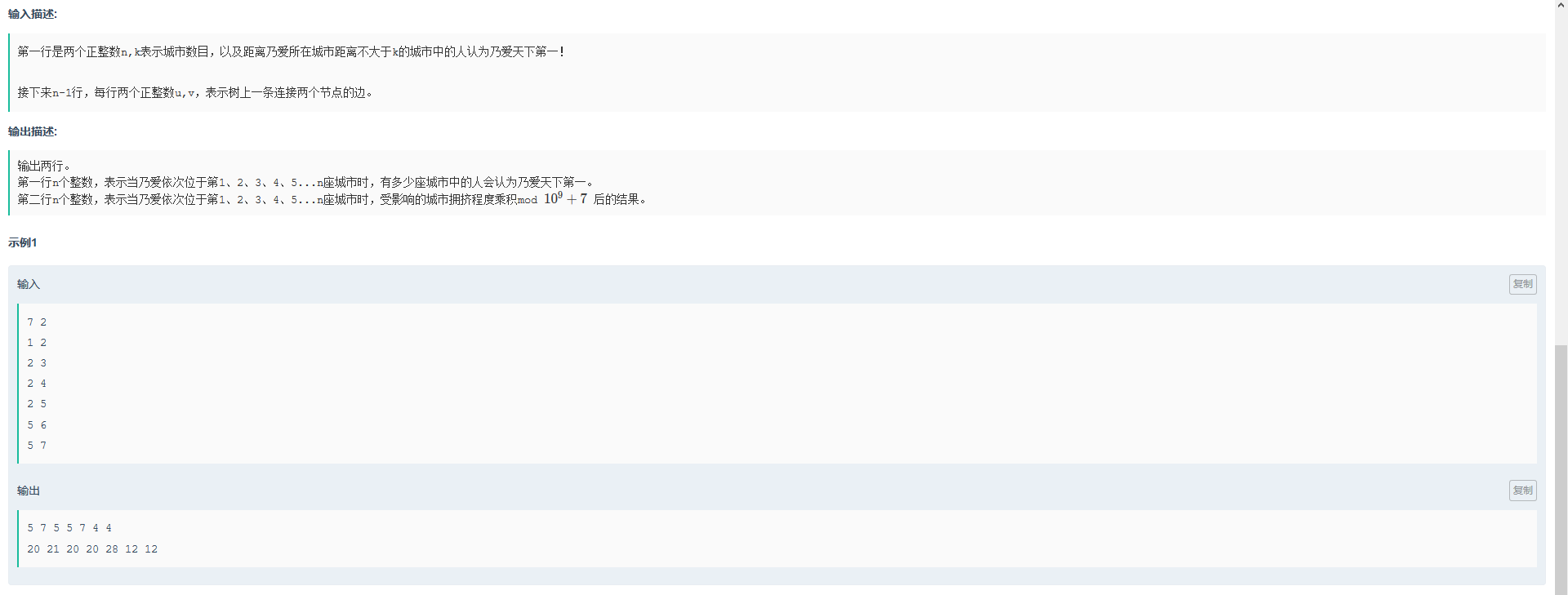

题解
\(80\%\)
随机树部分+链
直接暴力跑就完事了。
#include<bits/stdc++.h>
using namespace std;
template <typename Tp>
void read(Tp &x){
x=0;char ch=1;int fh;
while(ch!='-'&&(ch>'9'||ch<'0')) ch=getchar();
if(ch=='-') ch=getchar(),fh=-1;
else fh=1;
while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
x*=fh;
}
const int maxn=100007;
const int maxm=200007;
const int mod=1000000007;
int n,k;
int Head[maxn],to[maxm],Next[maxm],tot=1;
void add(int x,int y){
to[++tot]=y,Next[tot]=Head[x],Head[x]=tot;
}
int ans,tmp;
int aaa[maxn],bbb[maxn];
int dfs(int x,int fa,int dis){
int res=1;++ans;
if(dis==k) return res;
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(y==fa) continue;
res+=dfs(y,x,dis+1);
}
tmp=(long long)tmp*(long long)res%mod;
return res;
}
void solve(int x){
ans=0,tmp=1;
dfs(x,0,0);
aaa[x]=ans,bbb[x]=tmp;
}
int main(){
read(n);read(k);
for(int i=1,x,y;i<n;i++){
read(x);read(y);
add(x,y);add(y,x);
}
for(int i=1;i<=n;i++){
solve(i);
}
for(int i=1;i<=n;i++){
printf("%d%c",aaa[i]," \n"[i==n]);
}
for(int i=1;i<=n;i++){
printf("%d%c",bbb[i]," \n"[i==n]);
}
return 0;
}
\(100\%\)
换根DP。
小w的魔术扑克
问题描述