树
树是由结点或顶点和边组成的(可能是非线性的)且不存在着任何环的一种数据结构。
基本概念:
1)兄弟结点——拥有同一个父结点的结点;
2)孩子、双亲——结点的子树的根称为该节点的孩子,相应地,该节点称为孩子的双亲;
3)结点的度——一个结点所包含子树的数量;
4)树的度——该树所有结点中最大的度;
5)叶子结点——树中度为零的结点,也叫终端结点;
6)结点的层数——从根结点开始算,根结点是第一层,依次往下。
7)树的深度——树中结点的最大层数
8)有序树——树中的各结点的子树(兄弟结点)从左到右按一定次序去排列的树;
9)森林——m(m>=0)棵互不相交的树的集合。

存储结构:
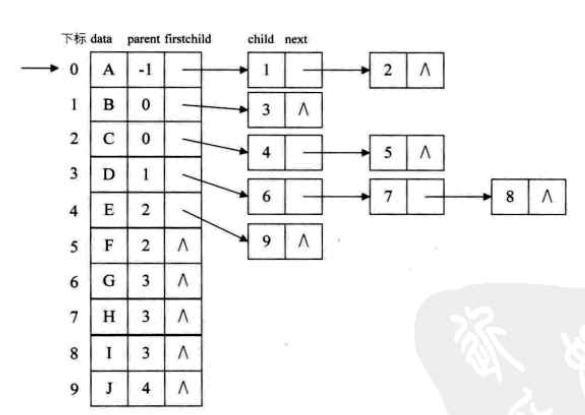
1)双亲表示法——在每个结点的结构中,附设一个字段记录其双亲结点在数组中的位置
结点结构如图:  ,data是数据域,存储节点的数据信息,parent是指针域,存储该节点的双亲在数组中的下标
,data是数据域,存储节点的数据信息,parent是指针域,存储该节点的双亲在数组中的下标
/*树的双亲表示法节点结构定义*/ #define MAX_TREE_SIZE 100 typedef int TElemType /*树结点数据类型,目前暂定为整型*/ typedef struct PTNode/*结点数据结构*/ { TElemType data; /*结点数据*/ int parent; /*双亲位置*/ }PTNode; typedef struct/*树结构*/ { PTNode nodes[MAX_TREE_SIZE]; /*结点数组*/ int r; int n; /*根的位置和结点数*/ }

2)孩子表示法,每个结点有多个指针域,其中每个指针都指向一颗子树的根结点。
方法一:

data是数据域,degree为度域,存储该结点孩子结点个数,child1到childd是指针域,用来指向该结点的孩子结点
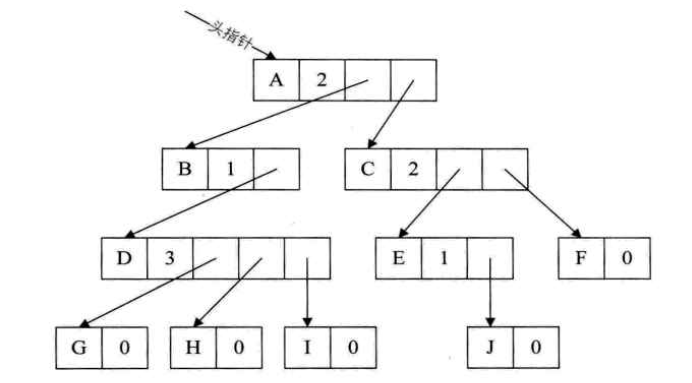
方法二:把每个结点的孩子结点排列起来,以单链表作存储结构,则n个结点n个孩子链表,如果是叶子结点则此单链表为空。然后n个头指针又组成一个线性表,采用顺序存储结构,存放进一个一维数组中。
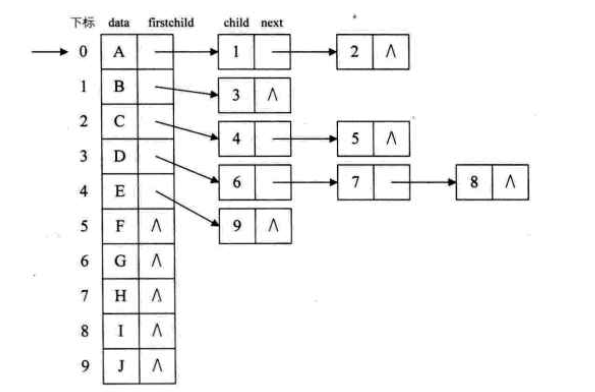
孩子结点:
child是数据域,用来存储某个结点在标头的数组中的下标。next是指针域,用来存放存储指向某结点的下一个孩子结点的指针
表头数组的表头结点 :
data是数据域,存储某结点的数据信息。firstchild是头指针域,存储该结点的孩子链表的头指针
双亲表示法和孩子表示法综合即双亲孩子表示法
方法三:孩子兄弟表示法,任意一棵树,他的结点的第一个孩子如果存在就是唯一的,他的右兄弟如果存在也是唯一的,因此我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟

data是数据域,firstchild为指针域,存储该结点的第一个孩子结点的存储地址,righstib是指针域,存储该结点的右兄弟结点的存储地址。
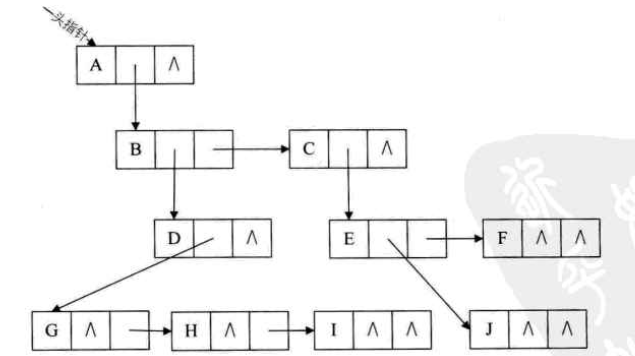
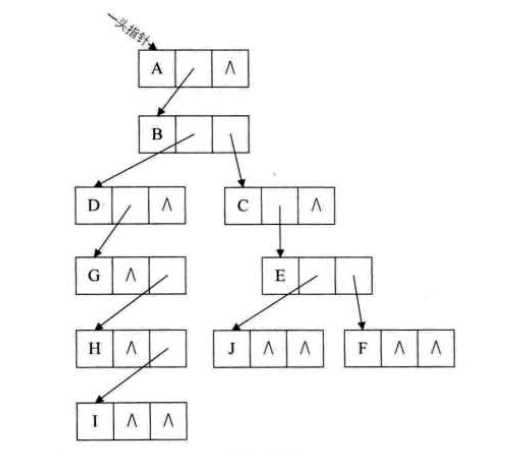
这样就把一棵复杂的树变成了一棵二叉树
树的种类
1)无序树:树中任意节点的子结点之间没有顺序关系,这种树称为无序树,也称为自由树;
2)有序树:树中任意节点的子结点之间有顺序关系,这种树称为有序树;
3)二叉树:每个节点最多含有两个子树的树称为二叉树;
4)完全二叉树
5)满二叉树
6)斜树
7)平衡二叉树
8)霍夫曼树:带权路径最短的二叉树称为哈夫曼树或最优二叉树;
二叉树
特点:
1)每个结点最多只有两个子结点,可以没有或者只有一个。
2)左子树和右子树是有顺序的,次序不能任意颠倒。
3)即使树中某结点只有一棵子树,也要区分左右子树
五种形态:1.空二叉树
2.只有一个根节点
3.根结点只有左子树
4.根结点只有右子树
5.根结点既有左子树又有右子树
特殊二叉树:
1.斜树:顾名思义所有结点都只有左子树或者右子树的二叉树。
2.满二叉树。所有分支结点都存在左子树和右子树。
3.完全二叉树。对一棵具有n个结点的二叉树按层序编号,如果编号为i(i∈[1,n])的结点与同样深度的满二叉树中编号为i的结点在树中位置完全相同,则称为完全二叉树
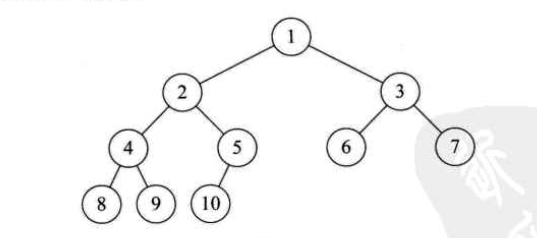
上图是一个完全二叉树
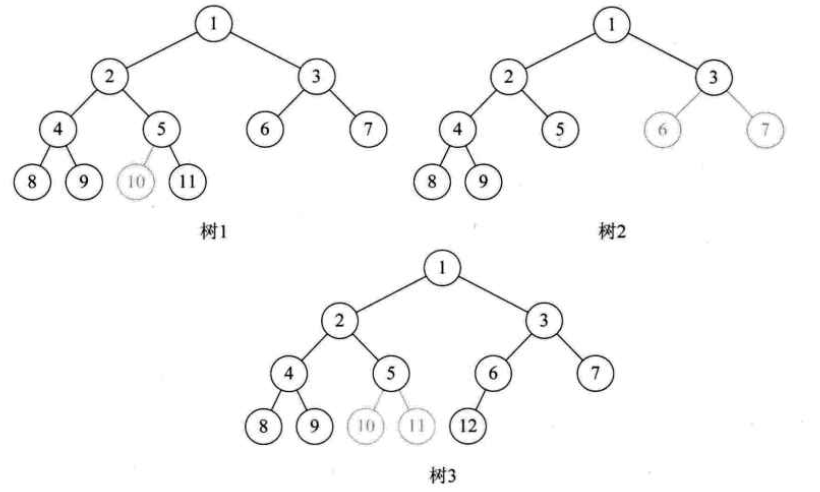
如图,树1,树2,树3按层序编号,序号均不连续,都不是完全二叉树。
二叉树性质:



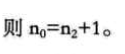



二叉树存储结构:
1)顺序存储结构:
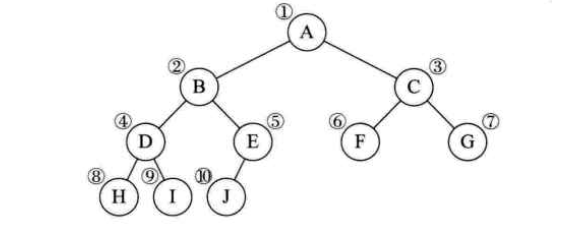
将二叉树存入数组,相应的下标对应相同的位置

由于二叉树定义严格,故顺序结构也可以表现出二叉树的结构(层序编号不能反映逻辑关系)
2)二叉链表

二叉树每个结点最多有两个孩子,故为他设计一个数据域和两个指针域
(孩子表示法,双亲表示法,孩子双亲表示法,孩子兄弟表示法)


